High School Physics - Newton's Law of Universal Gravitation
TLDRIn this informative talk, Mr. Fullerton explains Newton's law of universal gravitation, detailing how it quantifies the gravitational force between objects based on their masses and the distance between them. He demonstrates how to calculate the acceleration due to gravity on Earth's surface and the gravitational force between various objects in space, offering practical problem-solving tips and emphasizing the inverse square relationship in gravitational forces. The discussion is enriched with examples, including the gravitational interaction between asteroids, a meteor's changing gravitational force with Earth, and the forces between bowling balls and a falling object near Earth's surface.
Takeaways
- 🌍 Newton's law of universal gravitation states that all objects with mass attract each other with a force proportional to their masses and inversely proportional to the square of the distance between them.
- 📈 The gravitational force between two objects can be calculated using the equation: F = G * (m1 * m2) / R^2, where F is the force, G is the gravitational constant, m1 and m2 are the masses of the objects, and R is the distance between them.
- 🌗 To determine the acceleration due to gravity near the Earth's surface, we can use the Earth's mass and radius in the equation and find it to be approximately 9.8 meters per second squared.
- 🔢 The gravitational constant (G) is 6.67 × 10^-11 N(m/kg)^2.
- 📊 The relationship between gravitational force and distance is an inverse square law, meaning that as the distance between two objects increases, the force decreases rapidly.
- 🚀 When dealing with large objects, the distance between them should be measured from their centers of mass.
- 📝 Problem-solving hint: Substitute values for variables at the end of the problem to minimize errors and estimate the order of magnitude of the answer before calculation.
- 🪐 Example problem: The gravitational force between two asteroids, each with a mass of 50,000 kg and separated by 3,800 meters, is approximately 1.15 × 10^-8 N.
- 🌟 When a meteor moves from 16 Earth radii to 2 Earth radii from the center of the Earth, the gravitational force between the meteor and Earth becomes 64 times greater.
- 🎳 The gravitational force between two bowling balls, each with a mass of 7 kg and placed 2 meters apart, is approximately 8.17 × 10^-10 N.
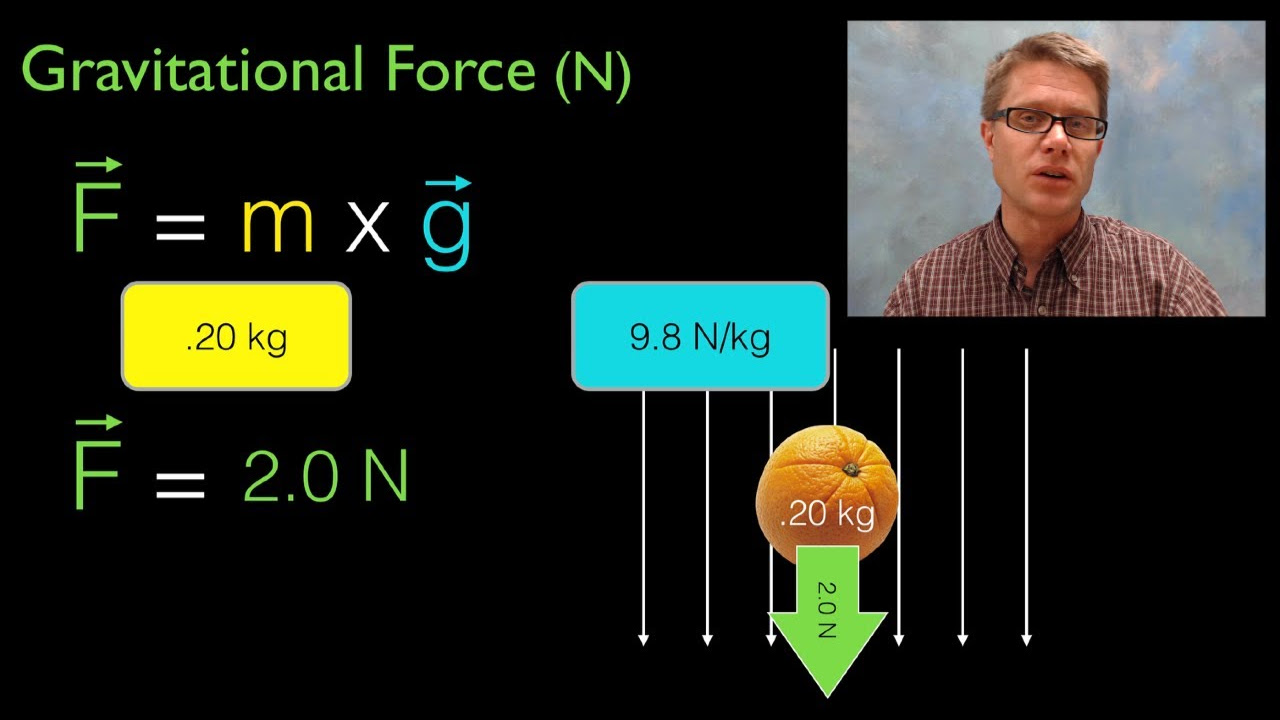
- 📉 A 2 kg object falling near Earth's surface experiences a gravitational force of 19.6 N, which is its weight.
Q & A
What is Newton's law of universal gravitation?
-Newton's law of universal gravitation states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them.
How is the gravitational force between two objects calculated?
-The gravitational force (F) between two objects is calculated using the equation F = G * (m1 * m2) / R^2, where G is the universal gravitational constant, m1 and m2 are the masses of the objects, and R is the distance between the centers of the two objects.
What is the value of the universal gravitational constant G?
-The universal gravitational constant G is approximately 6.674 × 10^-11 N(m/kg)^2.
How can we determine the acceleration due to gravity near the Earth's surface?
-We can determine the acceleration due to gravity (g) near the Earth's surface by rearranging the gravitational force equation and solving for g, using the mass of the Earth (M) and the Earth's radius (R). The equation becomes g = G * M / R^2.
What is the relationship between the distance between two objects and the gravitational force between them?
-The gravitational force between two objects is inversely proportional to the square of the distance between them. As the distance increases, the gravitational force decreases, and vice versa.
How does the gravitational force change when the distance between two objects is halved?
-When the distance between two objects is halved, the gravitational force between them increases by a factor of four (2^2 = 4), because the force is inversely proportional to the square of the distance.
What is the acceleration due to gravity on the surface of the Earth?
-The acceleration due to gravity on the surface of the Earth is approximately 9.8 meters per second squared.
How does Newton's third law relate to gravitational forces?
-Newton's third law states that for every action, there is an equal and opposite reaction. This means that if the Earth exerts a gravitational force on an object, the object exerts an equal and opposite gravitational force on the Earth.
What is the gravitational force between two asteroids with a mass of 50,000 kg each, separated by a distance of 3,800 meters?
-Using the formula F = G * (m1 * m2) / R^2, and substituting the given values (G = 6.674 × 10^-11 N(m/kg)^2, m1 = m2 = 50,000 kg, R = 3,800 m), the gravitational force between the two asteroids is approximately 1.15 × 10^-8 N.
How does the gravitational force between a meteor and the Earth change as the meteor moves from 16 Earth radii to 2 Earth radii?
-As the meteor moves from 16 Earth radii to 2 Earth radii, the distance changes from 16R to 2R. Since the force is inversely proportional to the square of the distance, the gravitational force becomes 64 times greater (because (1/2)^2 = 1/4, and the original force multiplied by 1/4 gives us 64 times the original force).
What is the gravitational force between two bowling balls, each with a mass of 7 kg, placed 2 meters apart?
-Using the gravitational force equation with G = 6.674 × 10^-11 N(m/kg)^2, m1 = m2 = 7 kg, and R = 2 m, the gravitational force between the two bowling balls is approximately 8.17 × 10^-10 N.
What is the magnitude of the gravitational force that Earth exerts on a 2 kg object falling freely near Earth's surface?
-The gravitational force that Earth exerts on the 2 kg object is equal to the object's weight, which is calculated as mass (m) times the acceleration due to gravity (g). So, the force is 2 kg * 9.8 m/s^2, which equals 19.6 Newtons.
Outlines
🌌 Introduction to Newton's Law of Universal Gravitation
This paragraph introduces the concept of Newton's law of universal gravitation, explaining that every object with mass exerts a gravitational pull on other objects. The force is directly proportional to the product of their masses and inversely proportional to the square of the distance between them. The speaker, Mr. Fullerton, aims to determine the acceleration due to gravity near the Earth's surface and how to calculate the gravitational force between any two objects. The explanation includes the formula for gravitational force, the value of the gravitational constant, and the importance of measuring distances from the center of mass for large objects. The paragraph also discusses how to calculate the acceleration due to gravity on Earth's surface using the Earth's mass and radius.
🚀 Gravitational Force Calculations and Problem Solving
In this paragraph, Mr. Fullerton continues the discussion on gravitational force by providing problem-solving examples. He explains how to calculate the gravitational force between two asteroids, a meteor moving closer to Earth, and the force between two bowling balls. The paragraph emphasizes the inverse square law relationship in gravitational force and offers practical tips for solving such problems, like estimating the order of magnitude before precise calculations and ensuring the final answer makes sense by comparing it to known quantities. The speaker also touches on Newton's third law, illustrating how forces act in equal magnitudes but opposite directions, and concludes with a simple example of calculating the gravitational force on an object near Earth's surface.
Mindmap
Keywords
💡Newton's law of universal gravitation
💡Acceleration due to gravity
💡Gravitational force
💡Center of mass
💡Inverse square relationship
💡Problem-solving hints
💡Meteor
💡Satellite
💡Bowling balls
💡Free fall
Highlights
Newton's law of universal gravitation is introduced, explaining that all objects with mass exert a gravitational pull on each other.
The gravitational pull is directly proportional to the product of the masses of the objects and inversely proportional to the square of the distance between them.
The universal gravitational constant, G, is defined as six point six seven times ten to the minus 11th Newton meter squared per kilogram squared.
The distance between large objects must be measured from their centers of mass, such as from the center of the Earth to the center of the Moon.
The acceleration due to gravity near the Earth's surface can be calculated using the mass of the Earth and its radius.
The acceleration due to gravity on Earth's surface is approximately 9.8 meters per second squared.
The inverse square relationship of gravity means that the force diminishes with the square of the distance between objects.
Problem-solving hints are provided, such as substituting values at the end of the problem and estimating the order of magnitude of the answer.
The gravitational force between two asteroids in space, each with a mass of 50,000 kilograms and separated by 3,800 meters, can be calculated using Newton's law.
When a meteor's distance from the center of the Earth changes from 16 to 2 Earth radii, the gravitational force between the meteor and Earth becomes 64 times greater.
A diagram is presented to illustrate that the Earth and a satellite attract each other with equal and opposite forces, in accordance with Newton's third law.
The gravitational force between two bowling balls, each with a mass of 7 kilograms and placed 2 meters apart, is calculated to be eight point one seven times ten to the minus ten Newtons.
The magnitude of the gravitational force that Earth exerts on a 2-kilogram object falling near the Earth's surface is 19.6 Newtons.
The law of universal gravitation can be used to calculate the gravitational force of attraction between any two objects, given their masses and the distance between them.
The importance of checking calculations against known or similar quantities to ensure accuracy and sensibility is emphasized.
A practical application of Newton's law is demonstrated through the calculation of gravitational forces in various scenarios, such as between asteroids, a meteor and Earth, and bowling balls.
The concept of the center of mass is crucial when dealing with large objects and their gravitational interactions, as highlighted by the example of Earth and the Moon.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: