Rates of Change
TLDRThis transcript offers an insightful lesson on the concept of rates of change and their significance in calculus. It begins by explaining the rate of change as the slope of a function, which describes how outputs change with respect to inputs. The script distinguishes between the constant slope of linear functions and the varying slopes found in nonlinear functions. It introduces the secant line as a tool to approximate the slope over an interval on a curve, leading to the concept of the average rate of change. The lesson progresses to the difference quotient, a more generic form of slope calculation that works for any interval on a curve. Finally, the transcript delves into the instantaneous rate of change, which is derived from the limit of the difference quotient as the interval between two points approaches zero, resulting in the slope of the tangent line at a specific point. This foundational understanding lays the groundwork for the study of derivatives in calculus.
Takeaways
- 📈 The rate of change for a function describes how outputs change with respect to inputs, which is essentially the concept of slope.
- 🔍 For linear functions, the slope (rate of change) is constant, meaning the rate of change does not vary between any two points on the graph.
- 📊 In the case of non-linear functions, the slope varies from point to point, indicating different rates of change along the curve.
- 🤔 To find the slope or rate of change for a non-linear function, a frame of reference is needed, which is often provided by an interval on the function.
- 📐 The average rate of change is calculated using the slope of the secant line over a closed interval, representing the average slope for that section of the curve.
- 📉 The difference quotient is a more generic form of slope that allows for the calculation of the slope between any two points on a curve, regardless of the interval.
- 🎓 As the distance between two points on a curve approaches zero, the secant line becomes a tangent line, and the rate of change becomes the instantaneous rate of change at a single point.
- 🧮 The instantaneous rate of change can be found by taking the limit of the difference quotient as the distance between the two points (H) approaches zero.
- ✅ The process of finding the instantaneous rate of change involves algebraic manipulation, simplification, and applying the concept of limits in calculus.
- 📋 Calculus, particularly in its early stages, is largely concerned with finding instantaneous rates of change, which are foundational to the concept of derivatives.
- 🚀 Understanding the concept of slope in various contexts (average and instantaneous) is crucial for further studies in calculus and its applications.
Q & A
What is the rate of change for a function?
-The rate of change for a function describes the rate at which the outputs change with respect to the inputs. It is essentially the slope of the function, which can be thought of as 'rise over run' where 'rise' is the change in y values and 'run' is the change in x values.
Why is slope considered a fundamental concept in understanding rate of change?
-Slope is a fundamental concept because it quantifies the rate at which one quantity changes with respect to another. In the context of functions, it describes how much the output (y) changes for a given change in the input (x), which is the essence of the rate of change.
How does the slope of a linear function differ from that of a nonlinear function?
-For a linear function, the slope is constant across the entire graph, meaning the rate of change is the same between any two points. In contrast, for a nonlinear function, the slope varies from one point to the next, indicating that the rate of change is not constant and can increase or decrease as you move along the curve.
What is a secant line and how is it used to find the slope of a nonlinear function?
-A secant line is a straight line that intersects a curve at two distinct points. It is used to approximate the slope of a nonlinear function over a specific interval by finding the average rate of change. The slope of the secant line through the endpoints of the interval represents the average rate of change for the curve over that interval.
How is the average rate of change calculated for a function over a closed interval?
-The average rate of change is calculated by finding the slope of the secant line that passes through the endpoints of the closed interval on the function's graph. It is determined by the formula (f(b) - f(a)) / (b - a), where 'a' and 'b' are the x-values of the interval endpoints, and f(a) and f(b) are the corresponding y-values (function values).
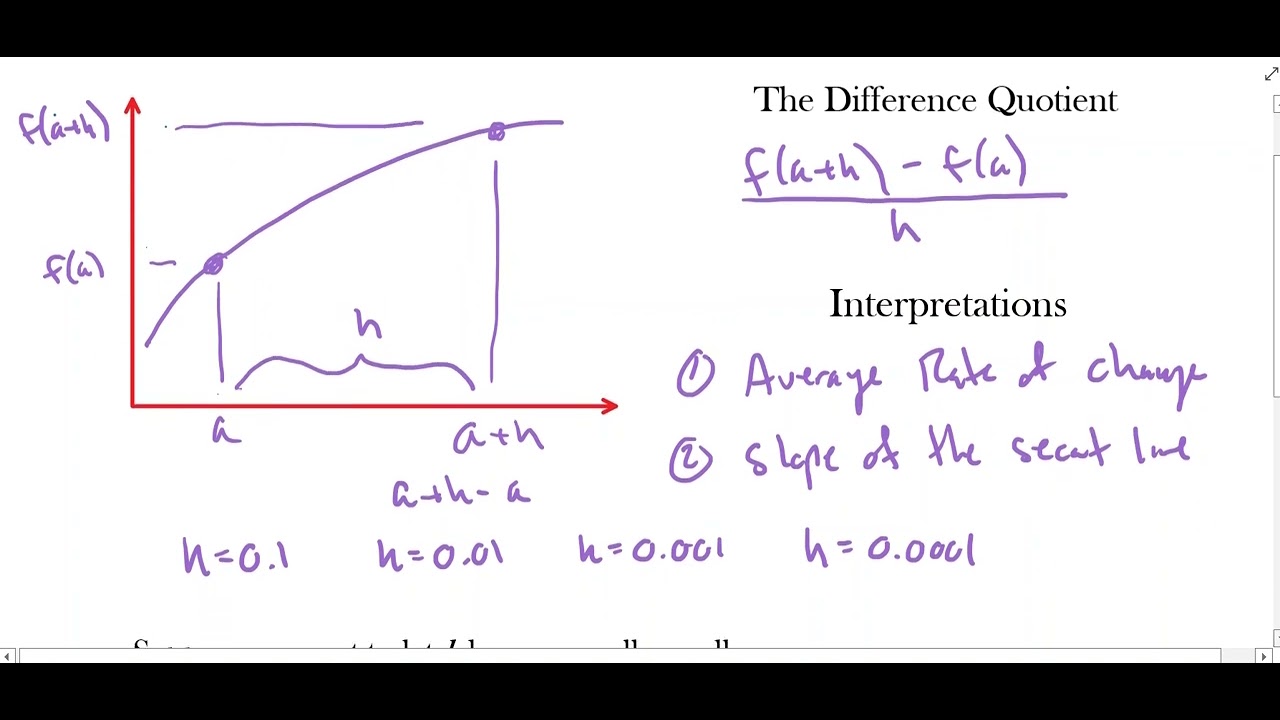
What is the difference quotient and how does it relate to the concept of slope?
-The difference quotient is another form of slope that uses a more generic notation and allows for the calculation of the slope between any two points on a curve. It is represented as (f(x + h) - f(x)) / h, where 'h' is the distance between the two points. The difference quotient is a way to find an equation for the slope without specifying exact x-values, making it versatile for any interval on a curve.
How does the limit of the difference quotient as h approaches zero define the instantaneous rate of change?
-The limit of the difference quotient as h approaches zero gives us the instantaneous rate of change, which is the slope at a single point on the curve. As h becomes infinitely small, the secant line through two points on the curve becomes a tangent line at a single point, and the slope of this tangent line represents the instantaneous rate of change at that point.
What is the significance of finding the instantaneous rate of change in calculus?
-Finding the instantaneous rate of change is significant because it allows us to determine the exact rate of change of a function at a specific point. This is a fundamental concept in calculus, as it leads to the definition of the derivative, which is a key tool for analyzing and understanding the behavior of functions and their rates of change.
How can you use the graph of a function to find the average rate of change over a given interval?
-You can use the graph of a function to find the average rate of change over a given interval by identifying the endpoints of the interval on the graph, determining the corresponding y-values, and then applying the formula for average rate of change. By counting the 'rise' (change in y-values) and the 'run' (change in x-values) between the endpoints, you can calculate the average slope for that section of the curve.
What is the relationship between the difference quotient and the derivative of a function?
-The difference quotient is a precursor to the concept of the derivative. The derivative of a function at a point is found by taking the limit of the difference quotient as the interval size (h) approaches zero. It provides the instantaneous rate of change at that point, which is the definition of the derivative in calculus.
Why is it necessary to simplify the difference quotient before finding the limit as h approaches zero?
-Simplifying the difference quotient before finding the limit as h approaches zero is necessary to avoid indeterminate forms and to make it possible to directly substitute h with zero. This simplification process often involves combining like terms and factoring out common factors, which prepares the expression for the limit calculation.
Outlines
📈 Introduction to Rates of Change and Slope
The first paragraph introduces the concept of the rate of change for a function, which is essentially the slope. It explains that the rate of change describes how outputs (often denoted as 'y' values) change with respect to inputs ('x' values). The paragraph clarifies that slope is a familiar concept, represented as 'rise over run,' and is used to quantify the movement from one point to another on a graph. It distinguishes between linear functions, where the slope is constant, and non-linear functions, where the slope varies.
🔍 Average Rate of Change and Secant Lines
The second paragraph delves into calculating the average rate of change for a non-linear function over a specific interval. It describes using a secant line intersecting the curve at two points to approximate the slope of the curve over that interval. The formula for the average rate of change is presented, using the function values at the endpoints of the interval and the corresponding x-values to find the slope of the secant line, which represents the average rate of change.
🔢 Calculating Average Rate of Change with Examples
The third paragraph provides a step-by-step guide to finding the average rate of change for a given function over a specified interval. It includes an example with a square root function, showing how to find corresponding y-values for given x-values and then use these to calculate the average rate of change. The paragraph emphasizes the importance of understanding the process and being able to visualize it on a graph.
🔄 Difference Quotient and Generalized Slope Calculation
The fourth paragraph introduces the difference quotient, a more generic form of slope calculation that doesn't rely on specific x-values but rather on a variable distance 'h' from an x-value. It explains that the difference quotient allows for the calculation of an equation to find the slope between any two points on a curve. The paragraph also demonstrates the notation and setup for using the difference quotient to find slope.
📐 Simplifying the Difference Quotient
The fifth paragraph focuses on simplifying the difference quotient for a quadratic function, f(x) = 4x^2. It walks through the algebraic process of finding f(x + h), subtracting f(x), and dividing by h. The paragraph emphasizes the importance of careful algebraic manipulation, especially when dealing with terms that include the variable 'h'.
🎓 Instantaneous Rate of Change and Limits
The sixth paragraph discusses the concept of instantaneous rate of change, which is the slope at a single point on a curve. It explains that as the distance 'h' between two points on a curve approaches zero, the secant line becomes a tangent line, and its slope represents the instantaneous rate of change. The paragraph outlines the process of finding this rate by taking the limit of the difference quotient as 'h' approaches zero.
🏞️ Applying the Instantaneous Rate of Change
The seventh paragraph illustrates how to apply the concept of instantaneous rate of change to a specific function, x^2 + 5, at a particular point, x = 2. It shows the steps to find the difference quotient, simplify it, and then evaluate the limit as h approaches zero to find the instantaneous slope at the given x-value. The paragraph concludes with a visual representation of the tangent line at the point of interest.
🧮 Rational Functions and Instantaneous Rate of Change
The eighth paragraph extends the concept of instantaneous rate of change to rational functions. It demonstrates the process of finding the difference quotient for a rational function, simplifying it, and then calculating the limit as h approaches zero. The paragraph concludes with an example calculation for the function f(x) = 2/(x - 4) at x = 1, showing the steps to find the instantaneous rate of change at that point.
🔑 The Significance of Calculus and Finding Slopes
The final paragraph summarizes the importance of the concepts covered, emphasizing that calculus, particularly in its first iteration (Calc 1), is fundamentally about finding instantaneous rates of change. It highlights that while the methods demonstrated were detailed, future topics will introduce more efficient ways to calculate these rates, with the next topic being the concept of a derivative. The paragraph encourages students to reach out for help if needed and looks forward to the next lesson.
Mindmap
Keywords
💡Rate of Change
💡Slope
💡Secant Line
💡Average Rate of Change
💡Instantaneous Rate of Change
💡Difference Quotient
💡Limit
💡Tangent Line
💡Derivative
💡Function
💡Linear vs. Non-linear Functions
Highlights
The concept of rate of change for a function describes how outputs change with respect to inputs, which is essentially the slope.
For linear functions, the slope is constant, whereas for nonlinear functions, the slope varies from one point to the next.
The slope, or rate of change, can be approximated on a nonlinear function by finding the slope of the secant line over a given interval.
The average rate of change is calculated over a closed interval and represents the average slope of the curve on that interval.
The formula for average rate of change is derived from the slope formula, using the endpoints of the interval on the curve.
The difference quotient is a more generic form of slope that allows for the calculation of slope between any two points on a curve.
The difference quotient involves finding the slope of a secant line using a variable distance 'h' from an x value.
The instantaneous rate of change is found by taking the limit of the difference quotient as 'h' approaches zero, which gives the slope of the tangent line at a point.
The instantaneous rate of change represents the slope at a single point on a curve, as opposed to the average rate of change over an interval.
The process of finding the instantaneous rate of change involves algebraic manipulation and simplification of the difference quotient.
Graphical representation can be used alongside algebraic methods to visualize and understand the concept of rate of change.
The difference quotient and its limit as h approaches zero are fundamental to the concept of derivatives in calculus.
The method for finding the instantaneous rate of change can be applied to various types of functions, including rational functions.
The process, while detailed and requiring careful algebraic steps, is a foundational aspect of calculus for determining rates of change.
The application of these concepts is crucial for understanding more complex calculus topics such as optimization and related rates.
The lecture provides a comprehensive foundation for students new to calculus, ensuring a solid understanding of rates of change.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: