Introduction to the Difference Quotient

Sun Surfer Math
6 Feb 202209:46
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the concept of the difference quotient, which is closely related to the average rate of change. The average rate of change is calculated by taking two points on a graph, finding the difference in their function values, and dividing by the difference in their x-values. The difference quotient is a variation of this formula that allows for the calculation of the average rate of change when the second point is not known, but a small distance 'h' between two points is given. The formula for the difference quotient is f(a + h) - f(a) / h, where 'a' is the known point and 'h' is the small distance. The script illustrates the process using a function f(x) = x^2 + 1, showing how the difference quotient can be used to find the average rate of change over an interval and the slope of the secant line between two points. By adjusting the value of 'h', the script demonstrates how the difference quotient can provide a more precise estimate of the slope as 'h' becomes smaller.

Takeaways
  • 📈 The concept of the difference quotient is introduced as a method to find the average rate of change between two points on a graph.
  • 🔢 The formula for the difference quotient is (f(a + h) - f(a)) / h, which is a variation of the average rate of change formula.
  • ↔️ The difference quotient calculates the rate of change using a small distance h instead of a fixed second point.
  • 📉 The 'a's in the formula cancel out, simplifying to (f(a + h) - f(a)) / h, which is the key formula for the difference quotient.
  • 📚 The difference quotient is used to find the slope of the secant line between two points on a graph.
  • 📐 By drawing a secant line, the difference quotient provides its slope, similar to how the average rate of change formula does.
  • 📈 An example is given using the function f(x) = x^2 + 1 to demonstrate how to apply the difference quotient.
  • 🔧 The example shows how changing the value of h (e.g., from 0.01 to 0.001) affects the calculation of the average rate of change.
  • 📉 As h becomes smaller, the average rate of change approaches the instantaneous rate of change at a point.
  • 💡 The difference quotient is a precursor to the derivative, providing insight into how the rate of change varies as the interval between points decreases.
  • ➗ The calculation involves evaluating the function at a + h and a, then dividing the difference by h, as shown in the example with h = 0.01 and h = 0.001.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the introduction of the concept of the difference quotient and its relation to the average rate of change.

  • What is the formula for average rate of change?

    -The formula for average rate of change is (f(b) - f(a)) / (b - a), where f(b) and f(a) are the function values at points b and a, respectively.

  • How does the difference quotient formula differ from the average rate of change formula?

    -The difference quotient formula is f(a + h) - f(a) / h, where h is a small distance instead of a specific second point like b in the average rate of change formula.

  • What is the significance of the difference quotient?

    -The difference quotient is significant because it provides a way to find the average rate of change when the second point is not known, and it gives the slope of the secant line between two points.

  • How does the value of h affect the difference quotient?

    -The value of h, which represents a small distance, affects the difference quotient by making it more precise as h gets smaller. A smaller h value results in a more accurate approximation of the instantaneous rate of change.

  • What is the purpose of using a small value for h in the difference quotient?

    -Using a small value for h allows for a more accurate representation of the rate of change over an infinitesimally small interval, which can approximate the instantaneous rate of change as h approaches zero.

  • How does the difference quotient relate to the secant line?

    -The difference quotient gives the slope of the secant line between two points on a graph, which is the same as the average rate of change over that interval.

  • What is the example function used in the video to illustrate the difference quotient?

    -The example function used in the video is f(x) = x^2 + 1.

  • What are the interval points used in the example to calculate the difference quotient?

    -The interval points used in the example are 2 and 2.01, with h being 0.01.

  • What is the average rate of change over the interval from 2 to 2.01 according to the example?

    -The average rate of change over the interval from 2 to 2.01 is 4.01, which is also the slope of the secant line over that interval.

  • How does changing the value of h in the example affect the average rate of change?

    -When the value of h is changed to a smaller value (e.g., 0.001), the average rate of change over the interval from 2 to 2.001 becomes 4.001, which is a more precise approximation due to the smaller interval size.

  • What tool or website can be used to calculate the values in the difference quotient example?

    -Desmos is a tool or website that can be used to calculate the values in the difference quotient example and verify the results.

Outlines
00:00
📐 Introduction to Difference Quotient and Average Rate of Change

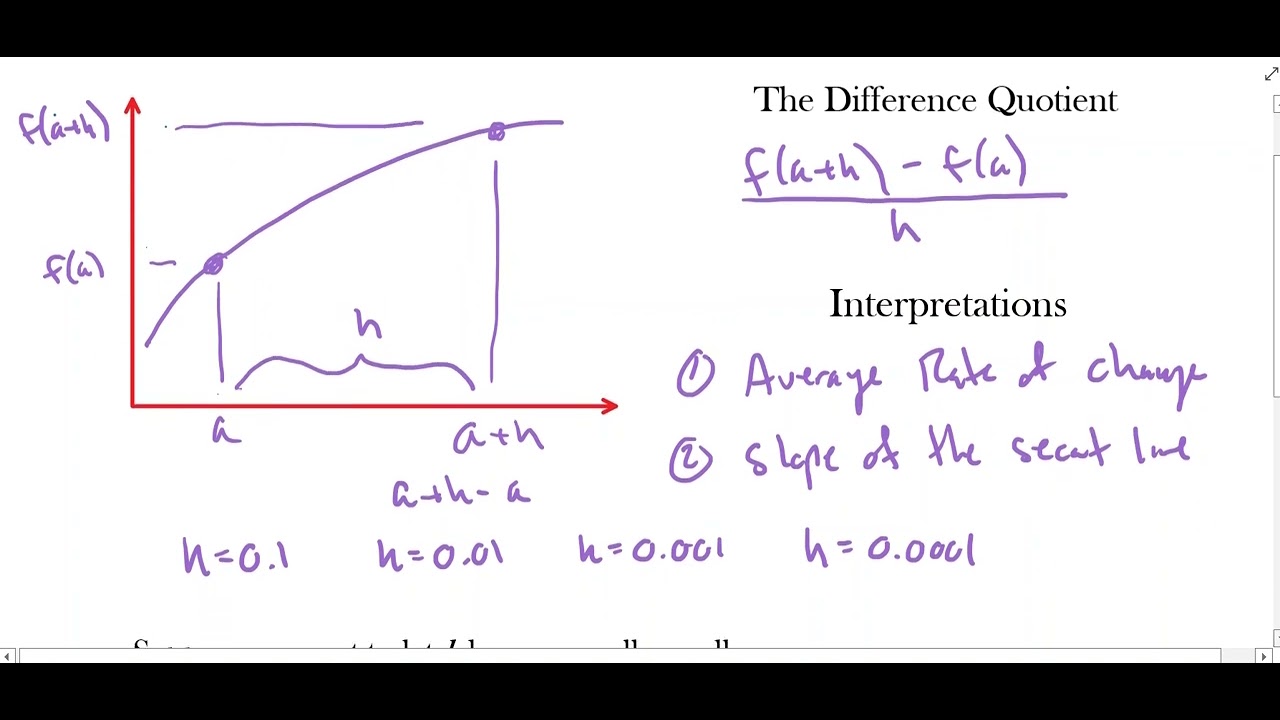
This paragraph introduces the concept of the difference quotient and its relation to the average rate of change. The speaker explains that instead of using two known points on a graph, the difference quotient involves a small, unknown distance 'h' from a known point 'a'. The formula for the difference quotient is presented as f(a+h) - f(a) / h, which simplifies to the function value at 'a' plus 'h' minus the function value at 'a', all divided by 'h'. This formula is crucial for finding the average rate of change between two points and for determining the slope of the secant line between them. An example is given using the function f(x) = x^2 + 1 over the interval from 2 to 2 plus a small increment 'h'.

05:02
🔍 Applying the Difference Quotient Formula with Varying 'h'

The second paragraph demonstrates the application of the difference quotient formula using the function f(x) = x^2 + 1. The interval considered is from 2 to 2.01 with h = 0.01. The speaker calculates the average rate of change over this interval using the difference quotient, resulting in a slope of 4.01 for the secant line. The paragraph then explores what happens when 'h' is reduced to an even smaller value, such as 0.001, leading to a new interval from 2 to 2.001. The calculation is repeated, yielding an average rate of change of 4.001 for the smaller interval. This illustrates the flexibility of the difference quotient in adjusting to different values of 'h' and its utility in approximating the instantaneous rate of change as 'h' approaches zero.

Mindmap
Keywords
💡Difference Quotient
The difference quotient is a mathematical formula used to estimate the rate of change of a function between two points. It is defined as the function value at a point 'a' plus some small change 'h', minus the function value at 'a', all divided by 'h'. In the video, it is used to find the average rate of change and the slope of the secant line between two points on a graph, illustrating its importance in calculus.
💡Average Rate of Change
The average rate of change is a concept that describes how a function value changes over an interval. It is calculated by taking the difference in function values at two points and dividing by the difference in the x-values of those points. The video explains how the difference quotient is a variation of this concept, allowing for the calculation of the rate of change when the second point is not fixed but varies by a small amount 'h'.
💡Function Value
A function value is the result one gets when a specific input is put into a function. For a function f(x), the function value at a point 'a' is denoted as f(a). In the video, the function values at points 'a' and 'a plus h' are used to calculate the difference quotient, which helps in understanding how the function behaves over a small interval.
💡Secant Line
A secant line is a straight line that intersects a function at two distinct points. In the context of the video, the difference quotient provides the slope of this secant line, which is a way to visualize the average rate of change over a specific interval. The slope of the secant line is a key concept in understanding how the function changes between two points.
💡Slope
Slope is a measure of the steepness of a line, indicating how much the y-values change with respect to the x-values. In the video, the slope of the secant line is found using the difference quotient, which is crucial for understanding the rate at which a function increases or decreases over an interval.
💡Graph
A graph is a visual representation of a function, showing how the function's values (y) relate to its inputs (x). The video uses a graph to demonstrate the concept of the average rate of change and the difference quotient by taking two points on the graph and finding the slope of the line between them.
💡Interval
An interval in mathematics is a continuous range of values within a function's domain. In the video, the interval is used to define the range over which the average rate of change is calculated, with the points on the interval being 'a' and 'a plus h'.
💡Desmos
Desmos is an online graphing calculator that allows users to plot functions and manipulate mathematical expressions. In the video, Desmos is suggested as a tool to calculate the function values and the difference quotient, highlighting its utility in visualizing and solving mathematical problems.
💡H (small increment)
In the context of the difference quotient, 'h' represents a small increment or change in the x-value of a point on the function. The video discusses how varying 'h' allows for an estimation of the function's behavior as 'h' approaches zero, which is a fundamental concept in the definition of a derivative in calculus.
💡Derivative
Although not explicitly mentioned in the transcript, the concept of the derivative is closely related to the difference quotient. The derivative of a function at a point is the limit of the difference quotient as 'h' approaches zero. It represents the instantaneous rate of change of the function at that point, which is a central theme in calculus.
💡Limit
The concept of a limit is fundamental in calculus and is related to the behavior of a function as its input approaches a certain value. While not directly mentioned in the script, the idea of taking 'h' to be very small in the difference quotient is a step towards understanding limits, which are used to define the derivative.
Highlights

Introduces the concept of the difference quotient and its relation to the average rate of change formula

Explains how to find the average rate of change using two points on a graph

Introduces a new variable 'h' to represent the unknown distance between two points

Derives the formula for the difference quotient as f(a+h) - f(a) / h

Points out that the difference quotient is a special case of the average rate of change formula

Highlights that the difference quotient is used to find the average rate of change when the second point is unknown

Mentions that h is typically a small value like 0.1, 0.01, 0.001, etc.

Explains that the difference quotient gives the slope of the secant line between two points

Provides an example using the function f(x) = x^2 + 1 and interval [2, 2+h]

Demonstrates calculating the difference quotient for h = 0.01 and h = 0.001

Shows that the average rate of change and slope of the secant line can be found using the difference quotient

Illustrates how changing the value of h affects the difference quotient and average rate of change

Uses Desmos to calculate and verify the difference quotient for different values of h

Points out that the difference quotient becomes the derivative as h approaches 0

Summarizes the key takeaways and practical applications of the difference quotient

Provides a clear, step-by-step explanation of the difference quotient concept

Uses a specific function and interval to make the concept more tangible and easier to understand

Demonstrates the calculation process for the difference quotient in a straightforward manner

Transcripts

Browse More Related Video

Average Rate of Change Using Difference Quotient

Introduction to the Derivative

1.3 - Average Rates of Change

Math 11 - Sections 1.3-1.4

More Difference Quotient Examples

Derivatives! The Limit Definition

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Difference QuotientAverage RateChange CalculationMathematicsFunction ValuesSecant LineSlopeDesmosEducational ContentMath TutorialConcept Explanation