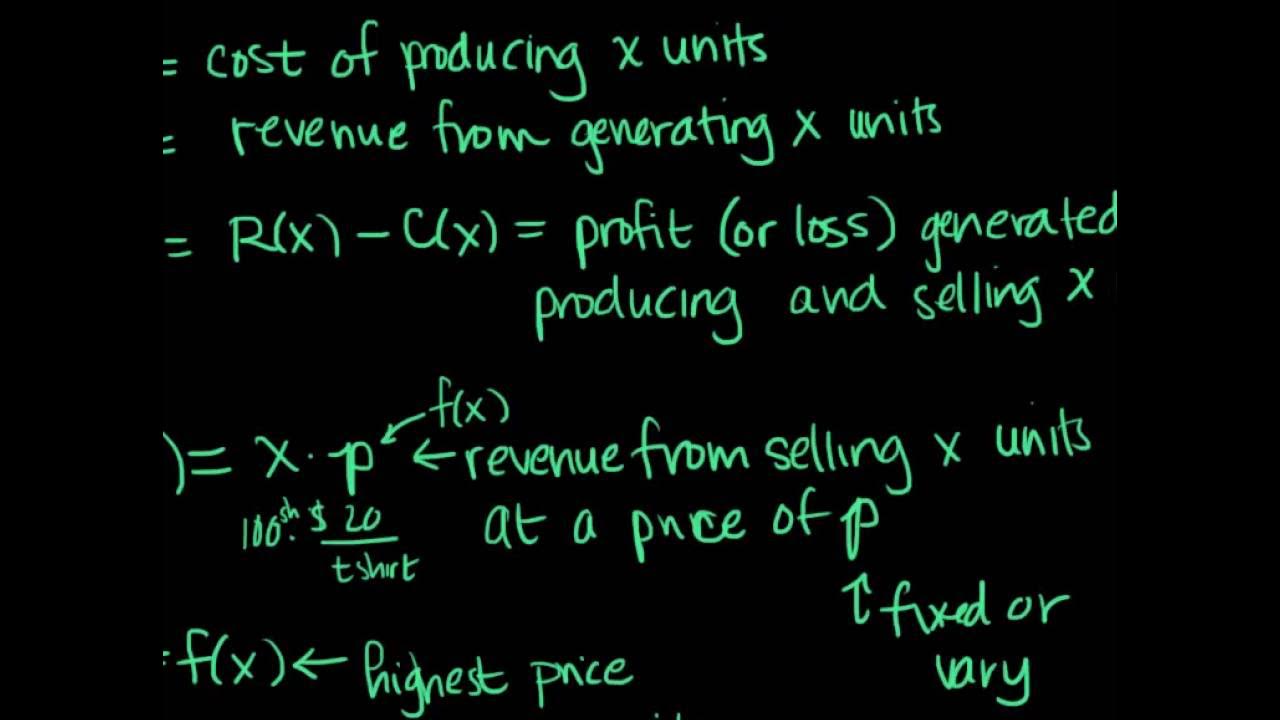BusCalc 22 Optimization
TLDRThis video script delves into the practical application of optimization problems, focusing on finding the optimum values of a function in real-world scenarios. The presenter explains that optimization involves maximizing or minimizing a function's output, such as profit or cost, and emphasizes the importance of reporting both the location and value of the optimum point. Through a series of examples, the video illustrates how to calculate profit maximization for a CEO of a disposable camera company, determine the maximum speed of a runner on a trail, and find the maximum area that can be enclosed with a given amount of fencing. The script also highlights the process of identifying critical points through derivatives and confirming these points as maximums or minimums using the second derivative. The examples are designed to be challenging, encouraging viewers to practice their optimization skills and think critically about the mathematical concepts involved.
Takeaways
- 📈 Optimization problems involve finding the best possible outcome, which can be either a maximum or a minimum depending on the context.
- 💰 In business, optimization often means maximizing profit, which is the revenue minus the costs, including both variable and fixed costs.
- 📐 The process of solving optimization problems typically involves setting up a function that represents the quantity to be optimized and then finding its critical points.
- 🧮 To find critical points, take the derivative of the function and set it equal to zero, solving for the variable in question.
- 📝 When reporting the solution to an optimization problem, provide both the input (independent variable) and the output (dependent variable), often in the form of a coordinate pair.
- 🔍 After finding a critical point, it's essential to determine if it corresponds to a maximum, minimum, or inflection point by analyzing the second derivative.
- 📉 A negative second derivative at a critical point indicates a maximum value, while a positive second derivative indicates a minimum.
- 🏃 For problems with a closed interval, always check the endpoints of the interval in addition to any critical points found within the interval.
- 🤔 Some optimization problems may require setting up a system of equations to express the constraints and then solving for the variables.
- 🧱 In real-world scenarios, such as enclosing an area with a fence, constraints like the amount of fencing available can be translated into mathematical equations.
- 📏 For geometric optimization problems, the dimensions of the object (like length and width) can be related to the total amount of a resource (like fencing) used.
- 📚 Practice is key to solving optimization problems, and working through examples from textbooks or similar resources can help build the necessary skills.
Q & A
What is the main focus of the video about optimization problems?
-The video focuses on optimization problems, specifically finding the optimum values (minimum or maximum) of a function with real-world applications, such as optimizing profit or cost.
Why is it important to report both the location and value when solving minimum or maximum problems?
-Reporting both the location (input x value) and the value (output y value) provides a complete answer to the optimization problem, showing exactly where the optimum occurs and what that optimum value is.
What is the relationship between the number of cameras sold (s) and the advertising dollars spent (m) in the first example?
-The number of cameras sold (s) is a function of the advertising dollars spent (m), represented as s = 10 * sqrt(m) + 50.
How is profit calculated in the context of the disposable camera company example?
-Profit is calculated as revenue minus expenses. Revenue is 15 times the number of cameras sold, and expenses include the variable cost of 4 dollars per camera and a fixed overhead cost of 900 dollars, plus the advertising cost.
What is the correct profit function in terms of advertising dollars (m) for the camera company?
-The correct profit function is p(m) = 110 * sqrt(m) - m - 350, after considering the advertising cost as an expense.
How do you determine the optimum amount of money to spend on advertising for the camera company?
-To determine the optimum amount, you find the critical points by taking the derivative of the profit function with respect to m, setting it to zero, and solving for m. Then, you verify that the critical point is a maximum by taking the second derivative and checking its sign.
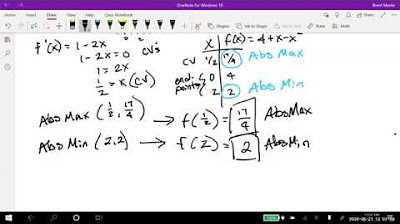
What is the maximum speed of the runner in miles per hour, and at what distance from the start of the trail does the runner hit this speed?
-The maximum speed is 7 miles per hour, and it occurs at the start of the trail (0 miles).
How is the area enclosed by a long pre-existing wall and fencing related to the amount of fencing used?
-The area is a function of the width of the fence, with the length being calculated based on the total fencing used (18 meters), which is 2 times the width plus the length.
What are the dimensions of the fencing that will give the maximum area enclosed by a pre-existing wall and three sides of fencing?
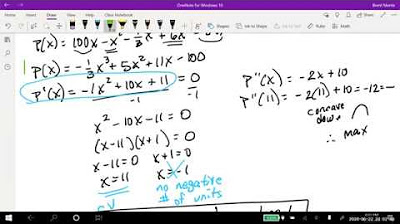
-The width that gives the maximum area is 4.5 meters, and the corresponding length is 9 meters.
What is the maximum area that can be enclosed with 18 meters of fencing, given a pre-existing wall on one side?
-The maximum area that can be enclosed is 40.5 square meters.
Why is it necessary to check the second derivative to confirm whether a critical point is a maximum or minimum?
-The second derivative helps determine the concavity of the function at the critical point. If the second derivative is negative, the function is concave down, indicating a maximum at that point. If it were positive, the function would be concave up, indicating a minimum.
Outlines
📈 Introduction to Optimization Problems
The video begins with an introduction to optimization problems, which are about finding the best possible outcome, either a minimum or a maximum, for a given function. The host explains that these problems are similar to finding extrema of curves but with a real-world application. The importance of reporting both the location and value of the optimum is emphasized, and the video sets out to teach the concept through examples.
🎯 Maximizing Profit for a Camera Company
The first example involves a CEO trying to maximize the profit of a disposable camera company. The relationship between the number of cameras sold (s) and the advertising dollars spent (m) is given by a function s = 10√(m + 50). The profit (p) is calculated by subtracting the variable cost (4 dollars per camera) and fixed costs (900 dollars overhead) from the revenue (15 dollars per camera). The video demonstrates how to find the optimal advertising spend to maximize profit, including the step of including advertising costs in the profit equation and using calculus to find the critical point and verify it as a maximum.
📊 Analyzing the Profit Function and Finding the Maximum
Continuing from the previous paragraph, the video shows the process of simplifying the profit function and finding its derivative. It then sets this derivative equal to zero to find critical points. The video also discusses the importance of the second derivative to confirm that a critical point is a maximum. The correct advertising spend to maximize profit is calculated to be 3025 dollars, and the resulting profit is found to be 2675 dollars.
🏃♀️ Runner's Speed Optimization
The second example deals with finding the maximum speed of a runner on a trail, given a function that models the runner's speed based on distance from the start. The video outlines how to find the derivative of the speed function and set it to zero to find critical points. It also covers evaluating the function at the endpoints of the interval and comparing these with the critical points to determine the maximum speed and the distance at which it occurs.
🧱 Enclosing a Rectangular Area with a Wall and Fencing
The third example involves finding the maximum area that can be enclosed with a pre-existing wall and 18 meters of fencing. The video explains how to set up the problem by expressing the length and width in terms of the total fencing used. It then shows how to find the critical points by taking the derivative of the area function and setting it to zero. The second derivative test confirms that the critical point corresponds to a maximum area, and the dimensions and area are calculated accordingly.
📏 Conclusion and Further Practice Advice
The video concludes with a brief mention of additional examples that are left for the viewer to practice. It advises that if viewers find the examples challenging, they should not be discouraged but instead work through easier examples from a textbook to build their understanding of optimization problems. The host wishes the viewers a good week, indicating the end of the video.
Mindmap
Keywords
💡Optimization Problem
💡Maximum and Minimum Values
💡Real World Modeling
💡Variable Cost
💡Fixed Cost
💡Profit Function
💡Derivative
💡Critical Points
💡Second Derivative Test
💡Coordinate Pair
💡Closed Interval
Highlights
Optimization problems involve finding the optimum values of a function, which can be either a minimum or a maximum depending on the goal.
Optimization problems are applicable to real-world scenarios, such as maximizing profit or minimizing cost.
When solving optimization problems, it's important to report both the location (input value) and the value (output or function value).
The first example involves a CEO optimizing company profit by finding the optimal amount to spend on advertising.
The relationship between the number of cameras sold (s) and advertising dollars (m) is modeled by the function s = 10√(m) + 50.
Profit is calculated as revenue minus expenses, which includes variable costs (cost per camera) and fixed costs (overhead).
The profit function, after including the cost of advertising, is p(m) = 110√m - 350 - m.
To find the optimum advertising spend, the derivative of the profit function is taken and set to zero to find critical points.
The second derivative test is used to confirm whether a critical point is a maximum by checking if the second derivative is negative.
For the camera company example, the optimal advertising spend is $3025 per month, resulting in a maximum profit of $2675.
The second example involves finding the maximum speed of a runner given a model that relates speed to distance from the start.
The runner's speed function is given by the equation speed = 1/10(-2m^3 + 9m^2 - 12m + 7).
Critical points for the runner's speed function are found by setting the first derivative equal to zero and solving for m.
The maximum speed occurs at the start of the trail (m = 0), with a speed of 7 miles per hour.
The third example is about maximizing the area enclosed by a pre-existing wall and fencing, with a total of 18 meters of fencing used.
The area function in terms of width is A(w) = 18w - 2w^2, and the critical point for maximum area is found by setting the first derivative to zero.
The maximum area is achieved with a width of 4.5 meters, resulting in an area of 40.5 square meters.
The video emphasizes the importance of understanding both the input values that yield the maximum and what the maximum value is in an optimization problem.
The presenter provides a caution that the last examples are challenging and encourages practice with easier examples if these are too difficult.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: