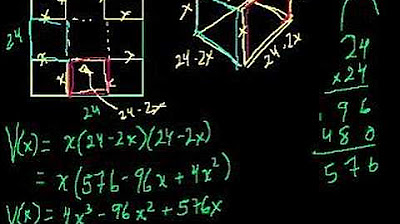Optimisation [IB Maths AI SL/HL]
TLDRThe video script outlines the process of optimization, focusing on maximizing or minimizing an equation, often related to variables such as speed, volume, or cost. The presenter explains the steps for optimization, which include formulating an equation with a single variable, finding its derivative, and setting it to zero to identify maximum or minimum points. A practical example is given involving cutting a cardboard into a box shape to maximize volume. The script details the mathematical process of deriving the volume equation in terms of a single variable 'x', and then differentiating it to find the critical points. Through factorization and the zero factor theorem, the presenter solves for 'x' and uses a sign diagram to confirm that one of the solutions corresponds to a maximum volume. The video concludes with a demonstration of how to use a calculator to find the maximum volume, emphasizing the flexibility of optimization techniques and their practical applications.
Takeaways
- 📝 **Optimization Defined**: The process of maximizing or minimizing an equation, such as those involving speed, volume, or cost.
- 🔍 **Key Steps in Optimization**: Identify an equation with a single variable, find its derivative, and set it to zero to locate the maximum or minimum.
- 📏 **Derivative Significance**: At the maximum or minimum, the derivative of the function equals zero, indicating a flat point on the graph.
- 🛠️ **Practical Example**: Cutting out squares from the corners of a cardboard to form a box, which is used to illustrate the optimization process.
- 📏 **Volume Calculation**: The volume of the box is expressed as a function of 'x', the length of the cut squares, to find the dimensions that maximize the volume.
- 🧮 **Derivative Calculation**: The derivative of the volume function with respect to 'x' is calculated to find the rate of change of the volume.
- ✏️ **Setting Derivative to Zero**: To find the maximum or minimum volume, set the derivative equal to zero and solve for 'x'.
- 🔢 **Solving for 'x'**: Factorization or the quadratic formula can be used to solve the equation resulting from setting the derivative to zero.
- 📉 **Second Derivative Test**: The second derivative test or sign diagram can be used to confirm whether a critical point is a maximum or minimum.
- 📊 **Graphing Utility**: Using a graphing calculator to visualize the function and find the maximum volume can simplify the process.
- 🔑 **Optimization Conclusion**: The value of 'x' that maximizes the volume of the box is identified, demonstrating the application of optimization in real-world scenarios.
Q & A
What is the primary goal of optimization?
-The primary goal of optimization is to maximize or minimize some equation, typically related to a variable like speed, volume, or cost, to find the conditions that yield the maximum or minimum value.
What is the first step in the optimization process?
-The first step in the optimization process is to find an equation for what you're looking for, ideally in terms of a single variable.
Why do we set the derivative of a function to zero when optimizing?
-We set the derivative of a function to zero because at the maximum or minimum of a function, the slope (derivative) is zero, indicating a flat point on the graph.
How does cutting out squares from the corners of a cardboard relate to optimization?
-Cutting out squares from the corners of a cardboard is a practical example used to illustrate the optimization process. It involves finding the optimal size of the squares to be cut out in order to maximize the volume of the resulting box.
What is the formula for the volume of the box made from a cardboard with cut-out corners?
-The volume (V) of the box is given by the formula V = x * (3 - 2x)^2, where x is the length of the side of the squares cut out from the corners.
What does the term dv/dx represent?
-The term dv/dx represents the derivative of the volume (v) with respect to the variable x, which shows how the volume changes as the size of the cut-out squares changes.
How do you find the maximum volume of the box using calculus?
-To find the maximum volume of the box using calculus, you would first find the derivative of the volume function (dv/dx), then set it equal to zero and solve for x. The value of x that satisfies this equation will give the maximum volume.
What is the significance of the quadratic formula in solving the optimization problem?
-The quadratic formula is used to find the x-values that make the derivative of the volume function equal to zero. These x-values are potential candidates for the maximum or minimum volume of the box.
How can you determine whether a critical point found is a maximum or minimum?
-You can determine whether a critical point is a maximum or minimum by using the second derivative test or by analyzing the sign of the first derivative (dv/dx) around the critical point.
What is the maximum volume of the box if x is 0.5?
-If x is 0.5, the volume of the box is maximized. The exact volume can be calculated by substituting x = 0.5 into the volume formula V = x * (3 - 2x)^2.
How can a calculator or graphing tool be used to find the maximum volume?
-A calculator or graphing tool can be used to graph the volume function and find the maximum value directly. By analyzing the graph or using the tool's maximum function, you can quickly determine the value of x that maximizes the volume.
Outlines
📐 Introduction to Optimization
The video begins by explaining the concept of optimization, which involves maximizing or minimizing an equation related to variables like speed, volume, or cost. The presenter emphasizes the importance of optimization in various real-life situations. The process involves finding an equation with a single variable, taking its derivative, and setting it to zero to find the maximum or minimum value. An example is introduced where cardboard is cut and folded to create a box, with the aim of expressing the box's volume in terms of a single variable, x.
🧮 Calculating the Volume of a Box
The presenter walks through the process of calculating the volume of a box created from a cardboard piece by cutting out small squares from the corners and folding it. The cardboard's initial size is considered, and then the dimensions of the resulting box are expressed in terms of x. The volume formula is derived as the product of length, width, and height, all in terms of x. The volume equation is then expanded and simplified to prepare for the next steps in optimization.
📈 Deriving the Volume Function and Setting it to Zero
The video continues with the process of differentiating the volume function with respect to x, resulting in an expression that shows how the volume changes with x. The derivative is then set to zero to find the critical points that could represent maximum or minimum volumes. The presenter simplifies the derivative equation and solves it for x, using both factorization and the quadratic formula, to find the values of x that maximize the volume.
🔍 Analyzing the Results and Maximizing Volume
After finding the critical points, the presenter uses a sign diagram to determine whether these points correspond to a maximum or minimum volume. It is concluded that one of the solutions, x equals 0.5, represents the maximum volume. The video also demonstrates how to use a calculator to graph the volume function and find the maximum volume directly. The process concludes with the understanding that an x value of 0.5 optimizes the box volume, confirming the effectiveness of the optimization technique.
Mindmap
Keywords
💡Optimization
💡Derivative
💡Volume
💡Maximize
💡Minimize
💡Cardboard Box
💡Equation
💡Variable
💡Factorizing
💡Quadratic Equation
💡Zero Factor Theorem
Highlights
The video discusses the concept of optimization, which involves maximizing or minimizing an equation.
Optimization is important for a variety of real-world situations.
The main steps for optimization are: 1) Find an equation with a single variable, 2) Take the derivative, 3) Set the derivative equal to 0.
The derivative equals zero at the maximum or minimum of a function.
A real-world example is provided involving cutting out squares from a piece of cardboard to form a box.
The volume of the box is expressed as a function of the side length x.
The volume equation is expanded and simplified to V = 4x^3 - 12x^2 + 9x.
The derivative dV/dx is calculated as 12x^2 - 24x + 9.
Setting dV/dx = 0 and solving yields two possible x values: x = 0.5 and x = 1.5.
Using a sign chart or calculator, it is determined that x = 0.5 corresponds to the maximum volume.
The maximum volume occurs when x = 0.5, which optimizes the box dimensions.
The process can be done by hand using algebraic techniques or using a calculator to graph the function.
The video demonstrates both manual and calculator-based methods for solving the optimization problem.
The volume equation and its derivative are key steps in the optimization process.
The choice of x value has a significant impact on the resulting volume of the box.
Making x too large or too small results in a smaller volume.
The optimization problem has practical applications in real-world scenarios.
The video provides a clear, step-by-step explanation of the optimization process.
Understanding the concept of optimization can be valuable in a range of disciplines.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: