Math1325 Lecture 10 1 - Relative Max & Min
TLDRThis lecture transcript delves into the concept of calculus as it applies to business and social sciences, focusing on optimization and the use of derivatives to find relative maxima and minima. The speaker explains that derivatives measure instantaneous change and can be used to analyze and optimize business functions such as cost, revenue, and profit. The lecture uses the metaphor of a mountain range to illustrate how to identify peaks (maxima) and valleys (minima) on a graph. It also covers how to find critical points by setting the derivative to zero and then determining whether these points represent maxima, minima, or points of inflection by examining the sign of the derivative before and after these points. The transcript walks through several examples, demonstrating how to calculate derivatives, find critical values, and use a calculator to analyze the behavior of the function around these critical points. It emphasizes the importance of understanding not just the calculation of derivatives, but also their practical application in identifying optimal business strategies.
Takeaways
- 📈 Derivatives are a measure of instantaneous change at a specific point and can represent the slope of a tangent line to a function's graph.
- 📊 Derivatives are used to find marginal functions such as marginal cost, revenue, or profit, which are crucial for business decision-making.
- 🔍 Businesses are interested in derivatives to understand how their sales, costs, revenue, or profits are changing and to optimize these variables.
- 🏔 Optimization often involves finding the maximum or minimum values of a function, which can represent the best or worst outcomes, like maximum profit or minimum cost.
- 📌 The process of optimization involves finding critical points where the derivative is zero or undefined, which can indicate relative maxima, minima, or points of inflection.
- 📐 A function's increase or decrease can be visualized through its graph, with the derivative's sign indicating the slope's direction at any given point.
- 🔢 To find the optimum values of a function, set its derivative equal to zero and solve for x, which gives the critical points where maxima or minima may occur.
- ↗️ After finding critical points, plug these x-values back into the original function to find the corresponding y-values, which represent the actual optimal points.
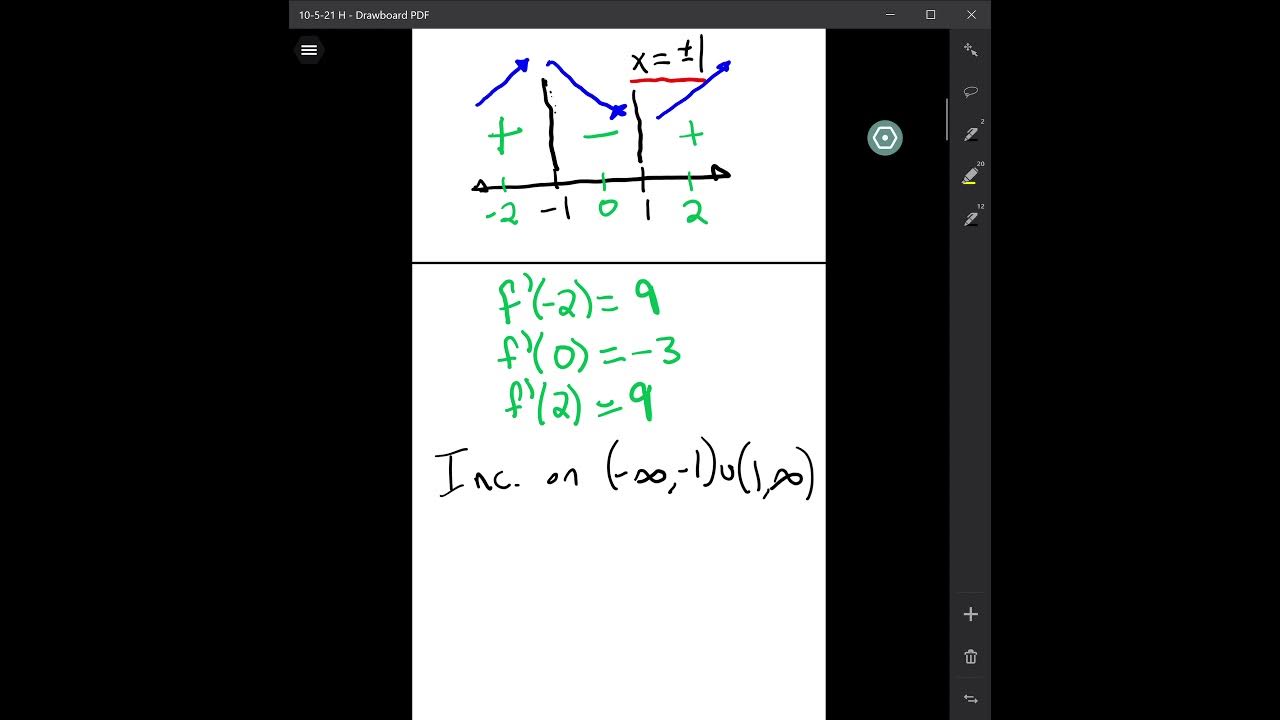
- ↕️ To determine whether a critical point is a maximum or minimum, examine the sign of the derivative before and after the point, using a table of values or a graph.
- 💡 Using a calculator's table function can help visualize the behavior of the function around critical points without having to plot the entire graph.
- ⚠️ It's important to remember that the derivative of a function can have points where it is undefined, which can indicate a sharp corner or a discontinuity in the function's graph.
Q & A
What is the primary role of derivatives in calculus?
-Derivatives are a measure of instantaneous change at a specific value and represent the slope of the tangent line to a function's graph at a given point.
How do derivatives relate to business and social sciences?
-Derivatives are used to analyze marginal functions such as cost, revenue, and profit, which are crucial for understanding how these variables change and for optimizing business operations.
What are critical values in the context of optimization?
-Critical values are the points where the derivative of a function equals zero. These points are potential locations for relative maxima or minima of the function.
How can one determine if a critical point is a maximum, minimum, or neither?
-By examining the sign of the derivative before and after the critical point. If the derivative changes from positive to negative, it's a local maximum; if it changes from negative to positive, it's a local minimum.
What is a horizontal point of inflection?
-A horizontal point of inflection is a point on a curve where the concavity changes but the function does not have a maximum or minimum at that point. The slope remains the same on either side of the point.
Why is it important to consider the behavior of a function around critical points?
-The behavior around critical points helps determine the nature of the point—whether it is a relative maximum, minimum, or neither—and is essential for optimization problems, such as maximizing profit or minimizing cost.
How can one find the derivative of a function?
-The derivative of a function can be found using various differentiation rules, such as the power rule, sum and difference rules, and the product rule, depending on the function's form.
What is the role of the second derivative in analyzing a function's behavior?
-The second derivative can help determine the concavity of a function and provides additional information about the nature of the critical points, such as whether they are points of inflection.
Why might a business be interested in the concept of instantaneous change?
-Businesses are interested in instantaneous change to monitor trends, such as whether sales are increasing or decreasing, and to make informed decisions about optimizing costs, revenues, and profits.
What is the significance of the slope of the tangent line in calculus?
-The slope of the tangent line at a point on a function's graph is represented by the derivative at that point. It provides information about the rate of change of the function at that specific point.
How can a calculator be used to assist in finding critical points and analyzing a function's behavior?
-A calculator can be used to compute derivatives, find where these derivatives equal zero, and analyze the function's values before and after critical points to determine if they correspond to maxima, minima, or points of inflection.
Outlines
📈 Introduction to Calculus in Business and Social Sciences
The first paragraph introduces the topic of the lecture, which is calculus for business and social sciences, specifically focusing on section 10.1 about relative maxima, minima, and curve sketching. The importance of derivatives in understanding instantaneous change and optimization is emphasized. Derivatives are described as measures of change and slopes of tangent lines, and their relevance to marginal functions such as cost, revenue, and profit is highlighted. The paragraph also touches on how businesses use derivatives to monitor changes and optimize operations, including maximizing profit while minimizing costs.
📚 Understanding Derivatives and Optimization
This paragraph delves into the concept of optimization, which involves finding the high or low points of a function, such as maximum profit or minimum cost. It uses the analogy of mountain ranges to illustrate how functions can have peaks and valleys. The paragraph explains the vocabulary and concepts related to derivatives, including increasing and decreasing functions, and how the sign of the derivative indicates the slope of the function. It also discusses how to identify relative maxima and minima by looking at the sign changes of the derivative and the slope at critical points.
🔍 Finding Optima Using Derivatives
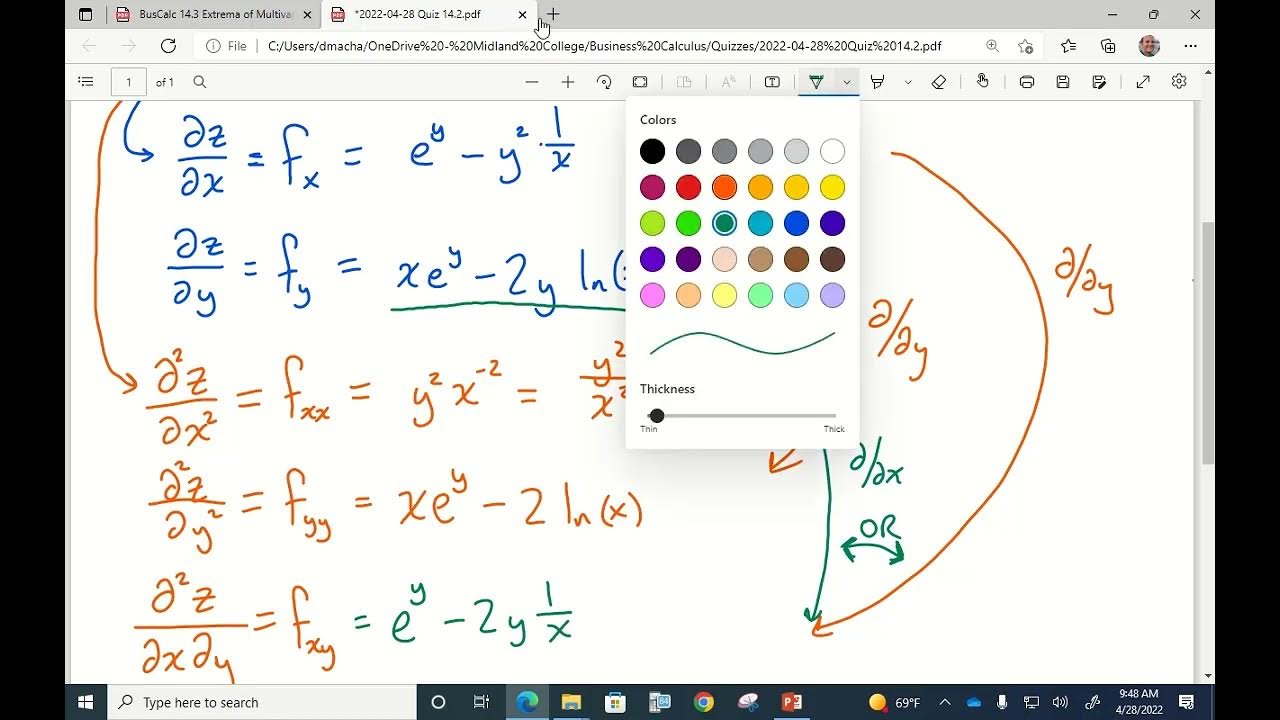
The third paragraph provides a step-by-step guide on how to find relative maxima and minima using derivatives. It starts with finding the derivative of a function, setting it equal to zero to find critical values, and then determining the corresponding Y values to find the optimal points. The paragraph also explains how to use a calculator to find critical points and how to interpret the results to determine whether a point is a maximum or minimum. It concludes with a reminder to check the original function, not the derivative, when determining the nature of the extremum.
🔢 Practical Examples and Calculator Usage
This paragraph presents practical examples of finding relative maxima and minima using derivatives. It discusses how to use a calculator to find critical points and how to determine if they correspond to maxima or minima by examining the behavior of the function around these points. The paragraph also addresses a common mistake of using the derivative instead of the original function when calculating Y values. It highlights the concept of a horizontal point of inflection, where the function changes from increasing to decreasing without a change in concavity. The paragraph concludes with a special case involving a rational expression with a radical in the denominator, explaining how to find points where the function does not exist.
Mindmap
Keywords
💡Derivative
💡Instantaneous Change
💡Marginal Functions
💡Optimization
💡Relative Maxima and Minima
💡Critical Values
💡Slope of a Tangent Line
💡Increasing and Decreasing Functions
💡Point of Inflection
💡Continuous Function
💡Quadratic Equation
Highlights
Derivatives are a measure of instantaneous change at a specific value and can be used to find the slope of a tangent line to a function's graph.
Derivatives are useful for marginal functions such as cost, revenue, and profit, which are crucial for business decision-making.
Businesses are interested in understanding how their sales, costs, revenue, and profits are changing and optimizing these factors for better performance.
Optimization involves finding the maximum or minimum values of a function, such as maximizing profit or minimizing cost.
The concept of relative maxima and minima is compared to identifying the peaks and valleys of a mountain range.
The derivative's sign (positive or negative) indicates whether a function is increasing or decreasing at a particular point.
A relative maximum or minimum occurs where the slope of the function changes from positive to negative or vice versa.
Critical values are points where the derivative is zero or undefined, indicating potential maxima or minima.
To determine if a critical point is a maximum, minimum, or neither, one must examine the sign of the derivative before and after the point.
The use of a calculator's table function can help visualize the behavior of the derivative around critical points.
A horizontal point of inflection is a point where the function's slope changes from concave up to concave down or vice versa, without a maximum or minimum.
When the denominator of a derivative includes a radical or a fraction, it's important to consider the points where the denominator could be zero.
Setting the numerator or a part of the derivative equal to zero can help find critical points where the function does not exist.
The process of finding relative maxima and minima involves taking the derivative, setting it to zero, finding critical values, calculating corresponding Y values, and analyzing the slope's behavior.
For functions with rational expressions, it's necessary to consider the behavior of the function at points where the denominator might be zero to avoid division by zero.
The lecture demonstrates the application of calculus in business and social sciences, particularly in optimizing business operations and outcomes.
The use of graphical and numerical methods, such as calculator tables, is emphasized for understanding and solving optimization problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: