Calculus AB/BC – 5.10 Introduction to Optimization Problems
TLDRIn this engaging calculus lesson, Mr. Bean introduces the concept of optimization, a topic with real-world applications that can challenge and expand the mind. He emphasizes the importance of optimization in various fields, including business, where he shares his personal experience of acing a calculus class that was filled with optimization problems. The lesson focuses on three key strategies: drawing a picture to visualize the problem, writing an equation to represent the optimization, and simplifying the equation to a single variable. Mr. Bean guides students through several examples, such as maximizing the product of two numbers, finding the closest point on a graph to a given point, creating a box with the largest possible volume from a piece of cardboard, and minimizing the amount of wire needed to connect two towers. The summary of the process involves setting up the equations and understanding the problem, with the actual solving of these problems to be covered in the next lesson. This approach not only teaches the mathematical techniques but also encourages students to appreciate the practical uses of calculus in everyday scenarios.
Takeaways
- 📚 The concept of optimization is about making the best or most effective use of a situation or resource, often aiming to maximize or minimize a particular outcome.
- 🔢 In mathematics, optimization problems typically involve finding the maximum or minimum value of something, like profit or material usage.
- 💡 Mr. Bean, a business major, found optimization particularly relevant and useful in business applications.
- 📈 The process of optimization involves three main strategies: drawing a picture if needed, writing an equation to be optimized, and ensuring the equation is in terms of a single variable.
- 📐 The first example in the script involves finding two numbers with a fixed sum (30) whose product is maximized, which is a classic optimization problem.
- 🧮 To solve optimization problems, one must often manipulate multiple equations to express the quantity to be optimized in terms of a single variable.
- 📐 The second example discusses finding the point on the graph of y = √x that is closest to the point (5,0), which involves minimizing the distance between two points.
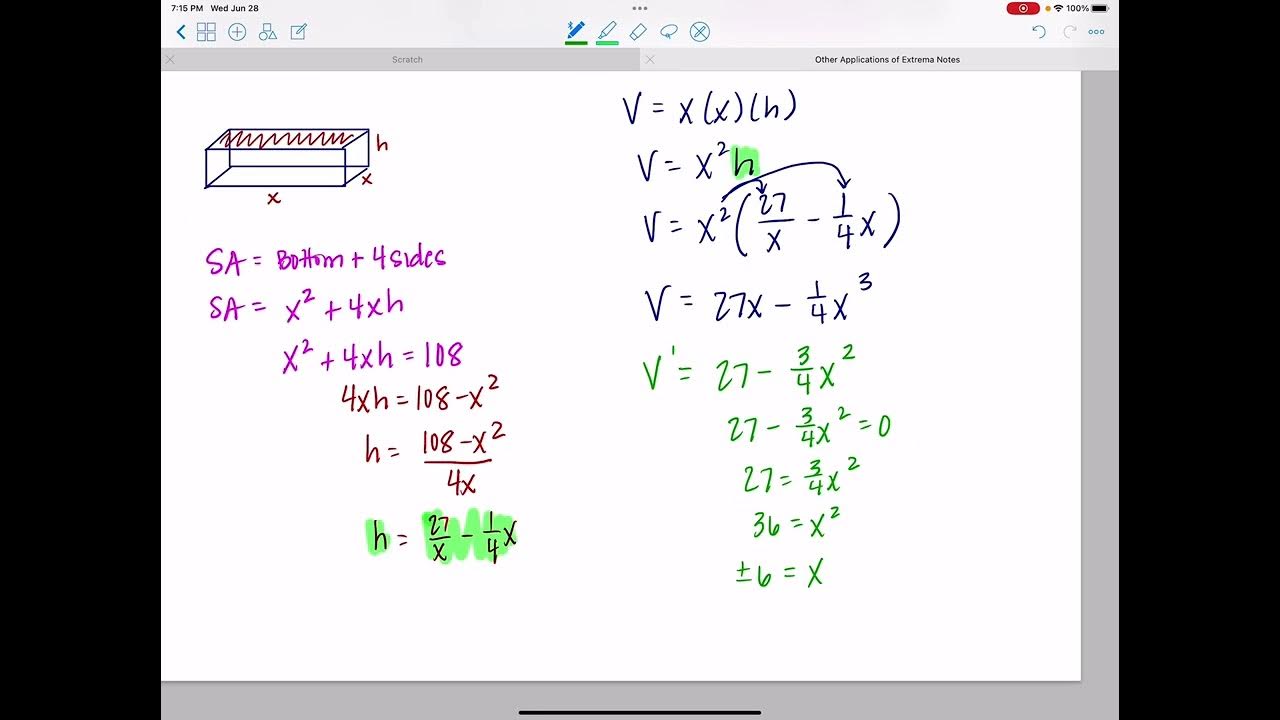
- 📦 The cardboard box problem illustrates how optimization can be used to find the dimensions of a box that maximize its volume, given certain constraints.
- 🏗️ The wire problem shows how optimization can minimize the amount of wire needed to connect two towers, using the Pythagorean theorem to express the total wire length.
- 📝 Setting up the correct equation is the most challenging part of solving optimization problems, and calculus techniques such as taking derivatives are used to find the optimal solution.
- 🔑 The key takeaway is that optimization is a fundamental concept in calculus with wide-ranging applications in real-world scenarios, from business to engineering.
- ✅ The next lesson will focus on solving these optimization problems, which involves taking the derivative of the single-variable equation and finding its critical points.
Q & A
What is the main topic of Mr. Bean's lesson?
-The main topic of Mr. Bean's lesson is optimization, which involves finding the maximum or minimum values in various scenarios.
Why does Mr. Bean consider optimization to be a challenging but exciting topic?
-Mr. Bean considers optimization challenging because it requires expanding one's mind to solve complex problems, and exciting due to its real-world applications in business and other fields.
What is the definition of 'optimize' in the context of the lesson?
-In the context of the lesson, 'optimize' means to make the best or most effective use of a situation or resource, often aiming to find a maximum or minimum value.
What are the three strategies Mr. Bean focuses on in the lesson?
-The three strategies Mr. Bean focuses on are: drawing a picture when needed, writing an equation to be optimized, and ensuring that the equation is in terms of a single variable.
How does Mr. Bean use calculus to find the maximum or minimum value in an optimization problem?
-Mr. Bean uses calculus by taking the derivative of the equation representing the optimization problem and setting it equal to zero to find the maximum or minimum value.
What is the first optimization problem presented in the script?
-The first optimization problem is to find two numbers whose sum is 30 and whose product is as large as possible.
How does Mr. Bean approach the problem of finding the point on the graph y = √x that is closest to the point (5,0)?
-Mr. Bean approaches the problem by using the distance formula, setting up an equation for the distance between the point on the graph and the point (5,0), and then expressing this in terms of a single variable to optimize.
What is the scenario described for the cardboard box problem?
-The scenario involves cutting out squares from the corners of a cardboard piece and folding it to create an open-top box. The goal is to determine the size of the squares to maximize the volume of the box.
What is the goal of the wire optimization problem involving two towers?
-The goal of the wire optimization problem is to find the position of a stake on the ground that would use the least amount of wire to connect to the tops of both towers.
How does Mr. Bean simplify the equation for the volume of the cardboard box?
-Mr. Bean simplifies the equation for the volume of the cardboard box by expressing the length, width, and height in terms of a single variable x, and then combining like terms and distributing x across the equation.
What is the key takeaway from Mr. Bean's lesson on optimization?
-The key takeaway is that the hard part of optimization problems is setting up the equations correctly. Once the equation is in terms of a single variable, calculus techniques such as taking the derivative and setting it to zero can be used to find the optimal solution.
Outlines
📚 Introduction to Optimization in Calculus
This paragraph introduces the topic of optimization, emphasizing its real-world applications and the challenges it presents to the learner. Mr. Bean, the speaker, highlights the importance of optimization in various fields, including business. He shares his personal experience as a business major and how he found optimization to be fascinating and useful. The paragraph outlines the basic strategy for tackling optimization problems, which includes understanding the concept of 'optimize', setting up equations to find maximum or minimum values, and focusing on the first three strategies: drawing a picture if necessary, writing an equation to be optimized, and ensuring the equation is in one variable.
🔍 Maximizing Product with a Given Sum
The focus of this paragraph is on a specific optimization problem where the goal is to find two numbers that add up to 30 and have the largest possible product. The process involves setting up an equation with two variables, x and y, representing the two numbers. Using the constraint that the sum of the numbers is 30, the equation is manipulated to express the product (p) in terms of a single variable, x. The resulting equation is then ready for further analysis, such as finding the maximum point by taking the derivative and setting it to zero, which will be covered in a subsequent lesson.
📏 Finding the Closest Point on a Function
This paragraph explores the concept of finding the point on the graph of y = √x that is closest to the point (5,0). The approach involves using the distance formula, which is derived from the Pythagorean theorem, to calculate the distance between the point on the function and the point (5,0). The distance is expressed as a function of x, and the goal is to minimize this distance. The paragraph concludes by noting that the next step would be to take the derivative of the distance function, set it to zero, and solve for x to find the point on the function that is closest to (5,0).
📦 Maximizing Volume with a Cardboard Box
The speaker presents a problem involving a cardboard piece that is to be cut and folded to create an open-top box with the largest possible volume. The cardboard has fixed dimensions, and squares of size x are cut from each corner. The volume of the box is then expressed in terms of x, the size of the cut squares. The paragraph details the process of setting up a cubic equation to represent the volume of the box and emphasizes the importance of expressing the volume in terms of a single variable. The next steps, which involve taking the derivative and finding the maximum volume, are to be covered in a later lesson.
📏 Minimizing Wire Length Between Two Towers
The final paragraph discusses an optimization problem where the goal is to find the position of a stake in the ground to minimize the total length of wire needed to reach the tops of two towers, given their heights and the distance between them. The problem involves using the Pythagorean theorem to express the lengths of the wires in terms of x, the horizontal distance from the stake to one of the towers. The total wire length is then set up as an equation in terms of x, which is to be minimized. The paragraph concludes by noting that calculus techniques will be used to solve for the minimum wire length in a future lesson.
Mindmap
Keywords
💡Optimization
💡Derivative
💡Product
💡Distance Formula
💡Volume
💡Pythagorean Theorem
💡Single Variable
💡Maximum
💡Minimum
💡Business Applications
💡Algebra 2
Highlights
Optimization is a challenging but exciting topic with real-world applications.
Optimization involves finding the maximum or minimum of a function, which can be applied to various scenarios like business.
The concept of optimization is to make the best or most effective use of a situation or resource.
The lesson focuses on three strategies: drawing a picture, writing an equation, and ensuring it's in one variable.
An example problem is introduced to illustrate the process of setting up an optimization problem involving the product of two numbers.
The importance of converting a multi-variable equation into a single-variable equation for optimization is emphasized.
Derivatives play a crucial role in finding maximum or minimum points in optimization problems.
A second example involves finding the point on the graph y=√x that is closest to the point (5,0).
The distance formula and the Pythagorean theorem are used to express the distance between two points in an optimization problem.
A practical application of optimization is demonstrated through a problem involving cutting a cardboard to create a box with the largest possible volume.
The volume of a box is expressed as a function of a single variable by relating the dimensions to the cut-out squares.
A cubic function is derived to represent the volume of the box for optimization purposes.
The process of setting up equations for optimization is identified as the most challenging part of solving such problems.
A final example problem involves using the least amount of wire to connect the tops of two towers.
The Pythagorean theorem is applied to express the total wire length as a function of a single variable.
The strategy of drawing a picture, writing an equation, and simplifying it to a single variable is a key approach to solving optimization problems.
The next lesson will cover solving the optimization problems set up in this lesson, including taking derivatives and finding solutions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: