Other Applications of Extrema
TLDRThe video script presents a detailed lesson on the application of extrema in optimization problems, moving beyond business contexts to include geometric and numeric examples. The instructor emphasizes the importance of defining variables, sketching diagrams, and writing equations to represent the problem accurately. The strategy involves finding critical numbers by differentiating primary equations that express the variable to be optimized. The lesson covers three main examples: maximizing the volume of an open box with a given surface area, minimizing the sum of two positive numbers with a fixed product, and minimizing the distance between a point on a parabola and a given point. The script is rich with mathematical steps, from setting up equations to differentiating and solving for extrema, providing a comprehensive guide for students to apply these concepts in various optimization scenarios.
Takeaways
- 📈 The lesson focuses on applying the process of finding extrema to optimization problems in various contexts, not just business-related ones.
- 📊 Optimization involves maximizing or minimizing variables such as profit, revenue, cost, or the number of units sold (X) and price (P).
- 📝 The general strategy includes defining variables, sketching a picture, writing equations, differentiating to find extrema, and considering the domain of the problem.
- 🔍 A primary equation is used to represent the variable being optimized, and a secondary equation may be needed to express it in terms of two variables for differentiation.
- 🟢 In the first example, the goal is to maximize the volume of an open box with a square base and a given surface area, leading to a geometric application of extrema.
- 🟠 The process involves setting up equations for surface area and volume, solving for one variable in terms of another, and then differentiating the resulting function to find the maximum volume.
- ✅ For the box volume maximization, the dimensions that produce the maximum volume are found to be a square base of 6 inches by 6 inches with a height of 3 inches.
- 🧮 In the second example, the task is to minimize the sum of two positive numbers where their product is a constant (288), resulting in a numeric application of extrema.
- 📐 The solution involves expressing one variable in terms of the other using the product equation, substituting into the sum to be minimized, and differentiating to find the minimum sum.
- 🔢 The minimum sum is achieved when the first number (X) is 12 and the second number (Y) is 24, leading to a minimum sum of 48.
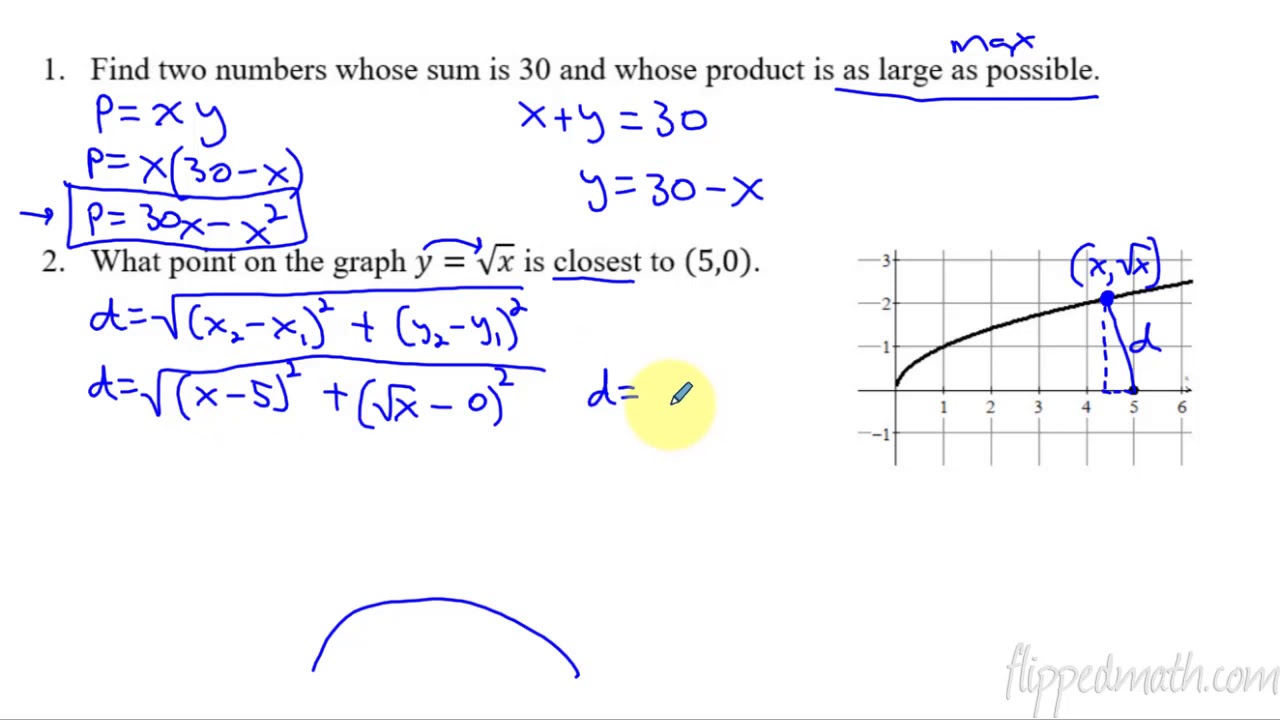
- 📍 The third example deals with minimizing the distance between a point on the graph of y = 4 - x^2 and a given point (0,2), which is a geometric application involving the distance formula.
- 🤔 The distance formula is squared and simplified before differentiating to find the critical points, which represent the points on the graph that are closest to the given point.
Q & A
What is the main focus of the lesson on other applications of extrema?
-The main focus of the lesson is to apply the process of finding extrema to optimization problems in different contexts, not necessarily business-related, and to maximize or minimize a particular value for a specific variable in the given problem.
What is the general strategy for solving optimization problems as described in the script?
-The general strategy includes defining variables, possibly sketching out a picture, writing an equation (or two), deciding which variable to optimize, differentiating the function to find critical numbers, being mindful of the domain, and ensuring the answer to the question asked is provided.
What is the primary equation in the context of the script?
-The primary equation is the one that involves the variable that is to be maximized or minimized. It is the equation that will be differentiated to find the extremum.
How is the secondary equation used in the optimization process?
-The secondary equation is used to express the primary equation in terms of just two variables, which is necessary for differentiation. It helps to eliminate one of the variables, making the primary equation simpler and more manageable for optimization.
In the example of maximizing volume, what is the manufacturer's goal?
-The manufacturer's goal is to design an open box with a square base and a surface area of 108 square inches, aiming to find the dimensions that will produce a box with the maximum volume.
What is the relationship between the surface area and volume equations in the box optimization example?
-The surface area equation is used as a secondary equation to express the height (h) in terms of the base dimension (x). This expression for h is then substituted into the volume equation, which is the primary equation being maximized.
What is the significance of considering the domain when solving optimization problems?
-Considering the domain is important because it ensures that the solutions are realistic and applicable to the problem. For instance, negative values or values outside the specified range might not make sense in the context of the problem and should be excluded.
In the script, how is the volume of the box calculated after finding the dimensions that maximize it?
-The volume is calculated by multiplying the length, width, and height of the box. After finding the dimensions (base as 6 by 6 inches and height as 3 inches), the volume is found to be 6 * 6 * 3, which equals 108 cubic inches.
What is the objective of the second example problem in the script?
-The objective of the second example problem is to minimize the sum of the second number and twice the first number, given that the product of two positive numbers is 288.
How does the script approach the problem of minimizing the distance between a point on the graph of y = 4 - x^2 and the point (0, 2)?
-The script approaches this by using the distance formula derived from the Pythagorean theorem, setting up an equation in terms of x and y, and then replacing y with 4 - x^2 to express the distance in terms of x alone. The derivative of this distance function is then found and set to zero to find the critical points that minimize the distance.
What is the final solution to the problem of minimizing the distance between the point on the graph of y = 4 - x^2 and the point (0, 2)?
-The final solution involves finding the x-values that minimize the distance, which are x = 0, x = √3, and x = -√3. The corresponding y-values are y = 4, y = 1, and y = 1, respectively. These points are all equidistant from the point (0, 2), providing the minimum distance.
Outlines
📈 Introduction to Optimization and Applications of Extrema
The video begins with an introduction to the topic of extrema and its applications in optimization problems. The focus is on maximizing or minimizing variables such as profit, revenue, cost, and the number of units sold or produced in various contexts. The general strategy involves defining variables, sketching a picture for clarity, writing equations, differentiating to find critical numbers, and considering the domain of the problem. The goal is to prepare viewers for their assignments, which will involve similar optimization problems.
🔍 Maximizing Volume with a Given Surface Area
The first example presented is a geometric application where a manufacturer wants to design an open box with a square base and a surface area of 108 square inches to maximize volume. The process involves sketching the box, writing an equation for the surface area, and another for the volume. By solving for one variable in terms of the other, a volume function in terms of a single variable is derived. Differentiating this function and finding critical numbers helps determine the dimensions that will produce the maximum volume. The video concludes with the calculation of the box's dimensions and the maximum volume.
📝 Minimizing the Sum of Two Positive Numbers with a Given Product
The second example deals with minimizing the sum of the second number and twice the first number, given that the product of two positive numbers is 288. The video demonstrates defining variables, setting up equations based on the given product, and using these to express the sum in terms of a single variable. Differentiating this single-variable function and solving for critical numbers allows finding the values of the two numbers that minimize the sum. The video ends with determining the specific numbers and the minimum sum.
📐 Minimizing Distance Between Points on a Graph
The third example involves minimizing the distance between a point on the graph of y = 4 - x^2 and the point (0, 2). The video explains using the distance formula derived from the Pythagorean theorem to establish an equation representing the distance between two points. By substituting the given function into the distance formula and differentiating the resulting equation, the critical points that minimize the distance are found. The video concludes with identifying the x-values that yield the minimum distance and calculating the corresponding y-values.
🔢 Dealing with Multiple Solutions in Distance Minimization
The video addresses a scenario where multiple points on the graph of y = 4 - x^2 are equidistant from the point (0, 2), resulting in more than one solution for the minimization problem. It discusses the importance of considering symmetry in the graph and acknowledges that while the assignment might ask for a single solution, there could be up to three points that are all at the minimal distance from (0, 2). The video advises on using decimal approximations for radicals or fractions when submitting assignments for grading purposes.
📚 Summary and Offer for Further Assistance
The video concludes with a summary of the algebraic work involved in the distance minimization problem and reassures viewers that the problems in their assignments will be aligned with the examples provided. It encourages viewers to reach out for extra help if needed and offers guidance on how to proceed if they encounter issues, including the use of Desmos for visualizing the problems and receiving feedback with clear directions.
Mindmap
Keywords
💡Extrema
💡Optimization
💡Derivative
💡Critical Numbers
💡Domain
💡Surface Area
💡Volume
💡Product of Numbers
💡Distance Formula
💡Parabolas
💡Rational Exponent
Highlights
The lesson focuses on applying the process of finding extrema to optimization problems in various contexts beyond business-related scenarios.
The general strategy involves defining variables, sketching a picture, writing equations, and differentiating to find maxima or minima.
The primary equation represents the variable to be optimized, while a secondary equation may be used to express it in terms of two variables.
Optimization problems can involve different types of variables such as profit, revenue, cost, and price.
The importance of considering the domain when solving for variables, as negative values may not be applicable in certain contexts.
An example of maximizing the volume of an open box with a square base and a given surface area is presented.
The process of differentiating the volume equation with respect to one variable and finding critical numbers is demonstrated.
The dimensions that produce the maximum volume for the box are calculated, emphasizing the need to consider practical constraints.
A second example involves minimizing the sum of a variable and twice another variable, given their product is constant.
The technique of expressing the sum equation in terms of a single variable using the product relationship is shown.
The concept of using the distance formula from the Pythagorean theorem to minimize the distance between two points is introduced.
The method of squaring the distance to avoid dealing with square roots when differentiating is explained.
An example of finding the point on the graph of a downward-facing parabola closest to a given point is explored.
The algebraic manipulation required to express the distance equation in terms of a single variable for differentiation is detailed.
The use of calculus to find the critical points where the derivative of the distance equation equals zero is demonstrated.
The consideration of symmetry in the graph to determine the points that are equidistant from a given point is highlighted.
The lesson concludes with a reminder to approximate radicals or fractions for assignment submissions to facilitate grading.
The instructor offers additional help and encourages students to reach out with questions, emphasizing support for understanding the material.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: