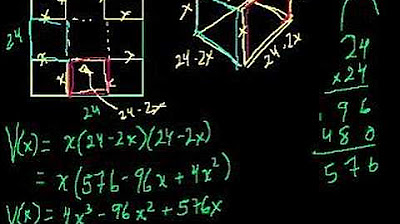optimization problems ultimate study guide (area & volume)
TLDRThe video script is an instructional guide on solving optimization problems from single-variable calculus. It covers various scenarios, including finding the dimensions of a rectangle with the smallest perimeter given a fixed area, a farmer using a limited amount of fencing to enclose the largest possible area, and the dimensions of a box constructed from a square piece of cardboard that maximizes volume. The guide uses mathematical concepts such as setting up constraint equations, taking derivatives, and applying the first and second derivative tests to find maximum and minimum values. The script is designed to help students and teachers understand and apply optimization techniques in solving word problems.
Takeaways
- 📝 The video is a tutorial on optimization problems in Calculus, specifically for single-variable calculus.
- 📈 The first problem discussed involves finding the dimensions of a rectangle with a fixed area of 1000 meters squared and minimizing the perimeter.
- 🤔 To solve word problems, the video suggests using the powerful words 'no' (what is known) and 'want' (what is desired).
- 📝 For the rectangle problem, the video demonstrates setting up the equation using the area formula and the constraint on the perimeter.
- 🧠 The video explains that to find the minimum or maximum of a function, one should take the derivative, set it to zero, and find critical numbers.
- 📊 The second problem is about a farmer with 24 feet of fencing wanting to create a rectangular field with one side along a river, maximizing the area.
- 🎨 The video shows how to use the given constraints to form an equation and then apply calculus to find the maximum area.
- 📝 The third problem involves a poster with specific margins and a fixed printing area, aiming to minimize the total area including margins.
- 📐 The video demonstrates how to incorporate the margins into the equation and use calculus to find the dimensions that result in the smallest area.
- 📝 The video also covers a problem about finding the dimensions of a rectangle with the largest area, given it lies on top of a parabola.
- 📝 Lastly, the video discusses optimizing the volume of a right circular cylinder inscribed in a sphere and a box made from a square piece of cardboard with an open top.
- 👨🏫 The video is intended to help students learn optimization techniques and encourages teachers to use the video and accompanying worksheet for their classes.
Q & A
What is the main topic of the video?
-The main topic of the video is optimization in Calculus, specifically focusing on single variable calculus problems.
What is the first problem discussed in the video?
-The first problem discussed is finding the dimensions of a rectangle with an area of 1000 square meters that has the smallest possible perimeter.
How does the video introduce the concept of optimization?
-The video introduces optimization by using the two powerful words 'no' and 'want', where 'no' represents what is known from the problem and 'want' represents the desired outcome or solution.
What is the second problem presented in the video?
-The second problem involves a farmer with 24 feet of fencing who wants to create a rectangular field with one side along a river, thus not requiring fencing. The goal is to maximize the area of the field.
How does the video approach solving the problems?
-The video approaches solving the problems by setting up mathematical equations based on the given constraints and desired outcomes, then using calculus to find the critical points and determine the maximum or minimum values.
What is the significance of the first derivative in optimization problems?
-The first derivative is significant in optimization problems because it helps identify critical points where the function could have a maximum or minimum value. Setting the first derivative equal to zero allows us to find potential solutions.
What is the role of the second derivative in optimization?
-The second derivative helps determine whether a critical point corresponds to a maximum, minimum, or neither. If the second derivative at a critical point is positive, the function is concave up and the point is a local minimum; if it's negative, the function is concave down and the point is a local maximum.
What is the third problem discussed in the video?
-The third problem involves finding the dimensions of a poster that will result in the smallest area given fixed dimensions and margins. The poster has a top and bottom margin of 6 centimeters each and side margins of 4 centimeters each, with the area of the printing material fixed at 284 square centimeters.
How does the video demonstrate the use of algebra and calculus in solving optimization problems?
-The video demonstrates the use of algebra to set up equations based on the problem constraints and objectives, and then uses calculus, specifically the first and second derivative tests, to find and verify the optimal solutions.
What is the fourth problem presented in the video?
-The fourth problem is about finding the dimensions of a rectangle with the largest possible area, with the additional constraint that the base of the rectangle lies on the x-axis and the two vertices are on a parabola defined by y = 12 - x^2.
How does the video conclude?
-The video concludes by summarizing the process of solving optimization problems using calculus, emphasizing the importance of understanding the constraints and objectives, setting up the appropriate equations, and applying calculus to find the optimal solutions.
Outlines
📚 Introduction to Optimization in Calculus
The video begins with an introduction to optimization problems in Calculus, specifically focusing on single-variable calculus. The speaker plans to cover questions from a textbook by James Stewart, encouraging viewers to take notes and attempt the problems before watching. The first problem involves finding the dimensions of a rectangle with an area of 1000 meters squared and minimizing the perimeter. The speaker emphasizes the importance of understanding the given information ('no') and the desired outcome ('want'), and introduces the method of taking derivatives to find minimum or maximum values.
📐 Solving the Rectangle Optimization Problem
In this section, the speaker continues to work through the rectangle optimization problem. They explain the process of labeling unknowns with variables, setting up the area equation based on the rectangle's dimensions, and expressing the perimeter in terms of a single variable. The speaker then demonstrates how to use calculus, specifically setting the derivative of the perimeter function to zero, to find the critical numbers that could represent minimum or maximum values. The solution process involves solving the derived quadratic equation and applying the second derivative test to confirm that the found value indeed represents a minimum.
🌾 Optimizing a Rectangular Field with Given Fencing
The speaker presents a second optimization problem involving a farmer with 24 feet of fencing who wants to create a rectangular field with one side along a river, thus not requiring fencing. The goal is to maximize the area of the field. The speaker sets up the problem by expressing the total length of the fencing in terms of the field's dimensions and then using the area equation to find a function of one variable. They proceed to find the maximum area by taking the derivative, setting it to zero, and solving for the critical number. The second derivative test confirms that the found value indeed yields a maximum area for the field.
🖼️ Poster Dimensions for Minimizing Material Usage
The third problem discussed in the video involves finding the dimensions of a poster that minimizes the amount of printing material used, given a fixed area and specific margin requirements. The speaker explains the scenario and sets up the equations for the total area of the poster, including the margins. They then transform the area equation into a function of one variable and use calculus to find the minimum area by taking the derivative and setting it to zero. The second derivative test is used to confirm that the critical number found indeed represents a minimum.
📦 Finding the Dimensions of a Box with Maximum Volume
The speaker moves on to a problem about finding the dimensions of a box with a maximum volume, given a fixed amount of material. The problem involves cutting squares from the corners of a larger square piece of cardboard and folding up the sides to form the box. The speaker sets up the equations for the volume of the box in terms of the side length of the cut squares and uses calculus to find the dimensions that yield the maximum volume. They also verify the solution using the first derivative test.
📦 Optimizing a Box with a Square Base for Volume
In this part, the speaker addresses a similar problem of optimizing a box with a square base for volume, but this time the box is inscribed in a sphere. The speaker explains the scenario and sets up the equations for the volume of the cylinder-shaped box in terms of the sphere's radius and the cylinder's dimensions. They use calculus to find the maximum volume and provide a detailed explanation of the process, including the product rule and chain rule for derivatives.
📦 Finding the Optimal Dimensions for a Box with a Given Volume
The speaker presents a problem about finding the dimensions of a box with a fixed volume and minimizing the surface area. The problem involves a square base and a height determined by the volume requirement. The speaker sets up the equations for the volume and surface area, transforms them into functions of one variable, and uses calculus to find the minimum surface area. They verify the solution using the first and second derivative tests and provide the dimensions that yield the optimal box design.
📦 Solving for the Box Dimensions with Maximum Volume
The speaker continues with another problem involving a box with a maximum volume, but this time the box is constructed from a square piece of cardboard with an open top. The speaker explains the construction process and sets up the equations for the volume of the box. They use calculus to find the dimensions that yield the maximum volume and verify the solution using the first derivative test.
📦 Minimizing Material for a Box with a Square Base and Fixed Volume
The final problem discussed in the video involves a box with a square base and a fixed volume, where the goal is to minimize the amount of material used. The speaker sets up the equations for the volume and surface area of the box and uses calculus to find the dimensions that minimize the surface area. They verify the solution using the first and second derivative tests and provide the optimal dimensions for the box.
Mindmap
Keywords
💡Optimization
💡Calculus
💡Derivative
💡Critical Numbers
💡Perimeter
💡Area
💡Second Derivative Test
💡Constraints
💡Volumes
💡Surface Area
Highlights
The introduction of optimization techniques in Calculus one class, specifically focusing on single variable calculus problems.
The use of two powerful words 'no' and 'want' to tackle word problems, emphasizing the importance of identifying known and desired variables.
The demonstration of finding the dimensions of a rectangle with a fixed area, showcasing how to minimize the perimeter through optimization.
The explanation of how to represent the area and perimeter mathematically, using variables to denote unknown quantities.
The application of calculus for optimization, specifically using derivatives to find critical numbers and determine minimum or maximum values.
The practical example of a farmer using a limited amount of fencing to enclose a field, illustrating how optimization can lead to maximizing area.
The use of constraint equations to transform optimization problems into solvable forms, allowing for the application of calculus.
The concept of second derivative test to verify whether a critical number represents a minimum or maximum, adding depth to the optimization process.
The presentation of a method to find the dimensions of a poster that minimizes the area, including the incorporation of margins.
The introduction of a problem involving a cylinder inscribed in a sphere, demonstrating the complexity and variety of optimization problems.
The detailed walkthrough of solving for the dimensions of a rectangle with the largest possible area, given specific constraints.
The explanation of how to calculate the volume of a cylinder and the optimization of its dimensions to achieve maximum volume.
The application of algebra and calculus to solve real-world problems, such as packaging and construction, showcasing the practicality of mathematical concepts.
The conclusion that emphasizes the video's purpose in helping viewers better understand and apply optimization techniques in their Calculus studies.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: