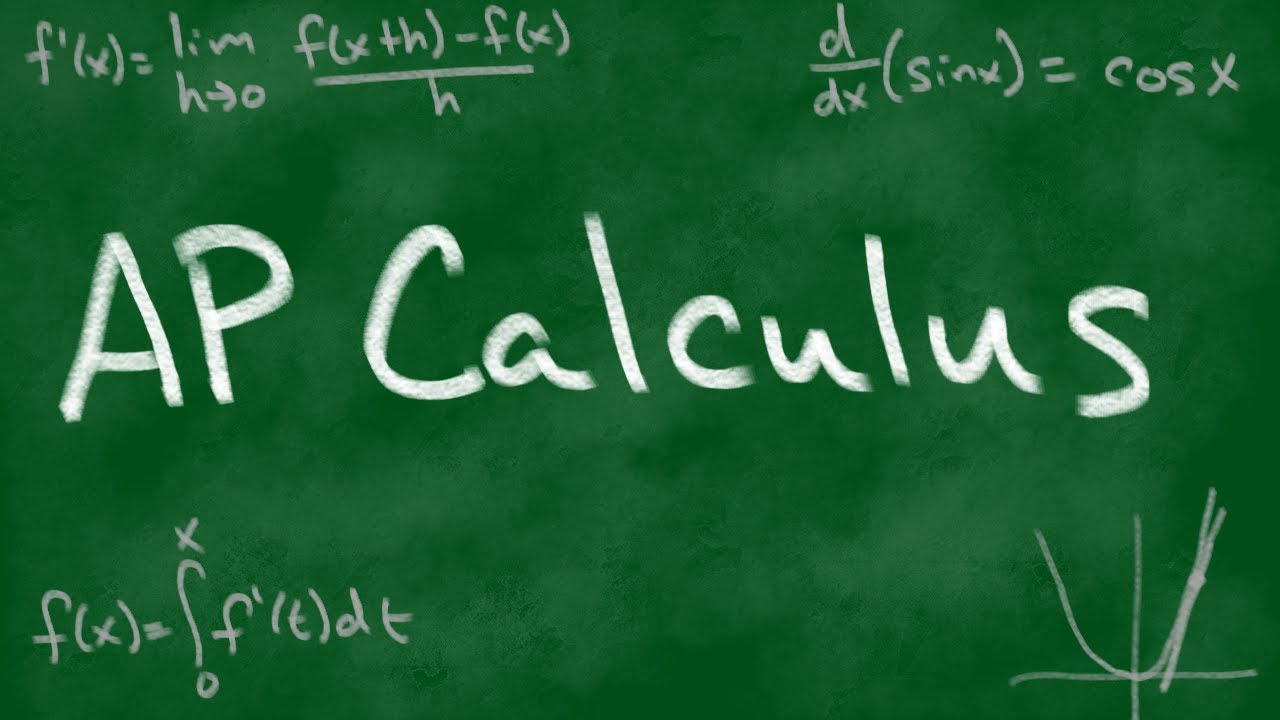2011 AP Calculus AB Free Response #6
TLDRIn this educational video, Alan from Bothwell Stem explores a free response question from the 2011 exam number six, focusing on the continuity and differentiability of a piecewise function F(x). Alan demonstrates that F(x) is continuous at x=0 by showing that the limit from the left equals the limit from the right, both resulting in the function value at x=0. He then explains that F(x) is not differentiable at x=0 due to differing slopes from either side. Alan continues by solving for the value of x where the derivative equals negative three, finding x to be -1/4 ln(3/4). Lastly, he calculates the average value of F(x) over the interval from -1 to 1, which he finds to be 13/8 minus cosine(-1) minus 1/8 e^(-4). The video concludes with a call to action for viewers to engage with the content and seek further assistance through Alan's free homework help on Twitch and Discord.
Takeaways
- 📌 The function F is defined piecewise, with different expressions for x < 0 and x > 0.
- 🔍 To show F is continuous at x=0, the limit from the left must equal the limit from the right, which both equal f(0).
- 🧮 Evaluating f(0) using the given definition yields f(0) = 1, confirming continuity at x=0.
- 🚫 F is not differentiable at x=0, as the left-hand and right-hand derivatives do not match.
- 🔑 The derivative of F, f'(x), is also piecewise defined, with expressions for x < 0 and x > 0.
- ⛔ The cosine function's value cannot exceed 1, hence there is no solution for f'(x) = -3 when x < 0.
- 🔢 For x > 0, setting f'(x) = -3 leads to the solution x = -1/4 * ln(3/4).
- 🧩 To find the average value of F, integrate f(x) over the interval from -1 to 1 and divide by the interval width.
- 📐 The average value calculation involves splitting the integral into two parts, one for each piece of the piecewise function.
- 🧾 After evaluating the integrals and combining terms, the average value is given as an algebraic expression.
- 🔄 It's important to check the algebra in the average value calculation to ensure accuracy.
- 📈 The presenter offers additional help for homework and questions on platforms like Twitch and Discord.
Q & A
What is the definition of continuity for a function at a given point?
-A function is continuous at a point if the limit of the function as it approaches from the left is equal to the limit as it approaches from the right, which is also equal to the function's value at that point.
What is the expression for the function F(x) as defined in the script?
-The function F(x) is defined piecewise, with F(x) = 1 - 2sin(x) for x ≤ 0 and F(x) = e^(-4x) for x > 0.
What is the value of F(0) according to the script?
-The value of F(0) is 1, as the sine of 0 is 0, and the expression simplifies to 1 - 2(0) = 1.
Why is the derivative of F(x) not defined at x = 0?
-The derivative of F(x) is not defined at x = 0 because the slopes from the left (-2cos(x)) and the right (-e^(-4x)) are not the same, indicating that the limit of the derivative does not exist at this point.
What is the condition to find the value of x for which the derivative of F(x) equals negative three?
-The condition is to solve for x in the equation -2cos(x) = -3 for x < 0 or e^(-4x) = 3/4 for x > 0.
What is the value of x for which the derivative of F(x) equals negative three?
-The value of x for which the derivative equals negative three is x = -1/4 * ln(3/4), which comes from solving e^(-4x) = 3/4.
What is the formula for calculating the average value of a function over an interval?
-The average value of a function F(x) over the interval [a, b] is given by (1/(b-a)) * ∫[a, b] F(x) dx.
How is the average value of F(x) calculated in the script?
-The average value of F(x) is calculated by integrating F(x) from -1 to 0 and from 0 to 1, then adding the results and dividing by the width of the interval, which is 2 in this case.
What is the final expression for the average value of F(x) found in the script?
-The final expression for the average value of F(x) is (13/8) - cos(-1) - (1/8) * e^(-4).
What is the significance of the average value of a function in calculus?
-The average value of a function over an interval represents the geometric mean of the function's values across that interval and is often used in applications involving areas and averages in physics and engineering.
What does the script suggest for further action after solving the problem?
-The script suggests checking the solution with a solution key, and for further engagement, it encourages viewers to leave comments, likes, or subscribe, and to follow the coach on Twitch and Discord for free homework help.
Outlines
📚 Continuity and Differentiability of Function F
In the first paragraph, Alan from Bothwell Stem, Coach delves into a mathematical problem from the 2011 exam number six. The focus is on demonstrating the continuity of a function F at x equals zero. To prove continuity, Alan shows that the limit of F as X approaches zero from the left is equal to the limit from the right. He calculates F(0) and uses the properties of sine and exponential functions to confirm that F is indeed continuous at zero. Alan then explores the derivative of F, noting that it is piecewise-defined and not differentiable at x equals zero due to differing slopes on either side. Lastly, he solves for the value of x where the derivative equals negative three, using the properties of cosine and exponential functions, and concludes with finding the average value of F over the interval from negative one to one, splitting the integral into two parts to accommodate the piecewise definition of F.
🧮 Calculation of the Average Value of Function F
The second paragraph continues the mathematical discussion, focusing on calculating the average value of the function F over the interval from negative one to one. Alan performs the integration required for the average value, splitting the interval into two parts due to the piecewise nature of F. He evaluates the integral from negative one to zero and from zero to one, carefully applying the limits of integration and the function's definition in each interval. After performing the integration, Alan simplifies the expression and divides by the width of the interval to find the average value. He concludes by checking his work against a solution key and summarizing the results, which include the continuity of F at x equals negative one-fourth natural log of three-fourths and the average value of the function, which he approximates as thirteen eighths minus cosine of negative one minus one-eighth e to the negative four. The paragraph ends with a note of encouragement and an invitation for viewers to engage with the content and seek further assistance through offered platforms.
Mindmap
Keywords
💡Function
💡Continuous
💡Limit
💡Derivative
💡Piecewise Defined Function
💡Sine Function
💡Exponential Function
💡Cosine Function
💡Average Value
💡Integral
💡Natural Logarithm
Highlights
The video discusses the free response question from the 2011 exam number six, focusing on the continuity and differentiability of a function F.
To prove continuity at x=0, the limits from the left and right must be equal to f(0).
For x<0, f(0) is calculated using the sine function, resulting in a value of 1.
For x>0, f(0) is calculated using e^0, which also equals 1, confirming continuity at x=0.
The derivative of F, f'(x), is a piecewise function with different expressions for x<0 and x>0.
The derivative does not exist at x=0, as the left and right-hand limits give different values.
The video demonstrates finding the value of x for which the derivative equals -3, using both parts of the piecewise function.
For x<0, it's shown that cosine(x) cannot equal 3/2, making that part of the equation inapplicable.
For x>0, the equation e^(-4x) = 3/4 is solved to find x = -1/4 ln(3/4).
The average value of F is calculated by integrating from -1 to 1 and dividing by the interval width.
The integral is split into two parts, one for the region where x<0 and another for x>0.
The final calculation for the average value is shown to be (13/8) - cos(-1) - (1/8)e^(-4).
The presenter suggests checking the algebra for potential errors before concluding the calculation.
The video concludes by confirming the continuity of the function and the value of x for the given derivative condition.
The presenter encourages viewers to leave comments, likes, or subscribe for more content and offers free homework help on Twitch and Discord.
The video ends with a teaser for the next video and an invitation to join the community for further assistance.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: