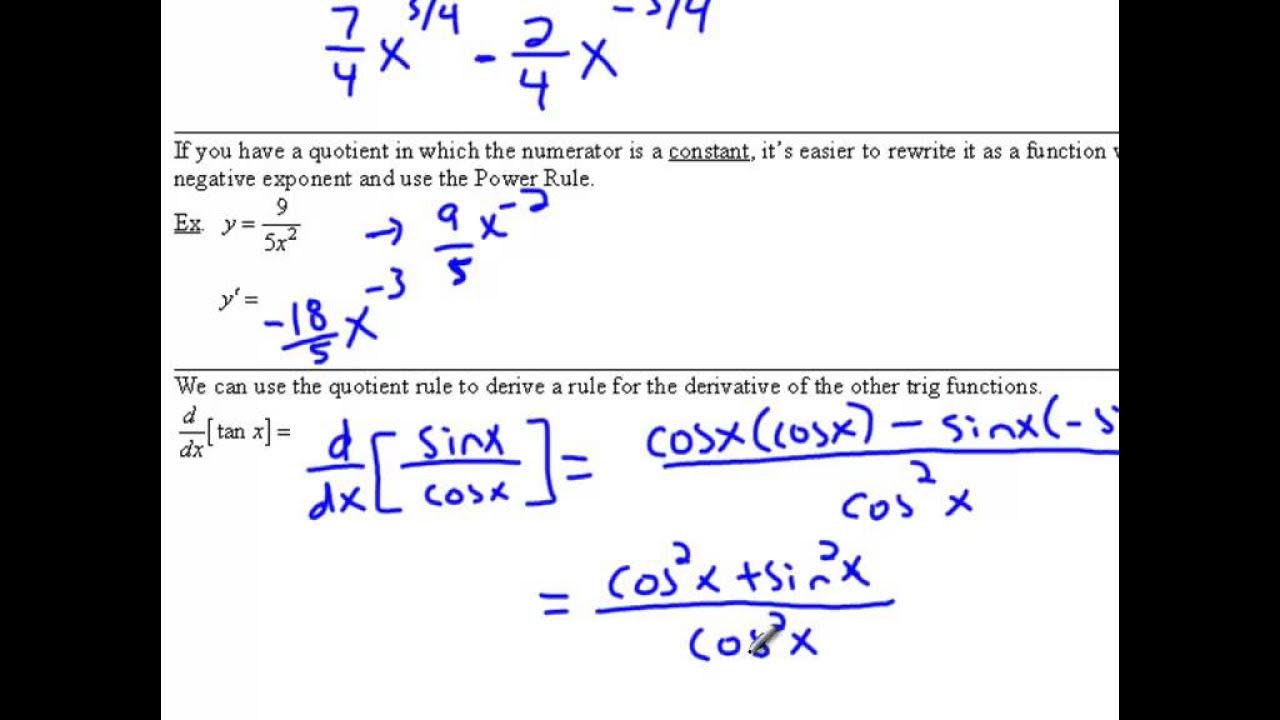Derivatives of Products and Quotients
TLDRThe video lesson focuses on the differentiation of products and quotients of functions, providing students with essential rules to simplify the process without resorting to the limit definition. The instructor introduces the product rule and quotient rule with their technical definitions, emphasizing the importance of these rules for differentiating functions that are products or quotients of other functions. The video demonstrates how to apply these rules through several examples, including finding the derivative of a function that is a product of two polynomials and the slope of a tangent line at a specific point. The instructor also discusses alternative methods, such as multiplying out functions before differentiation, which can be advantageous in certain scenarios. The lesson concludes with a reminder to students to consider all available options when differentiating, as the most straightforward method may vary depending on the function's form.
Takeaways
- 📚 Derivatives of products and quotients are essential calculus rules for differentiating functions without using the limit definition.
- 🤝 The product rule states that the derivative of a product of two functions is the derivative of the first times the second function plus the first function times the derivative of the second.
- 🧾 To remember the product rule, consider two functions f and g, and remember the formula as (f * g) + (f' * g) + (f * g') where f' and g' are the derivatives of f and g, respectively.
- 📉 The quotient rule is used for differentiating a function that is the quotient of two other functions, and it involves a difference of products divided by the square of the denominator.
- 🔢 When applying the product or quotient rule, it's crucial to be careful with algebraic manipulation to ensure accuracy, especially when combining like terms.
- 📈 The derivative of a function at a specific point gives the slope of the tangent line to the function's graph at that point.
- 🎓 For polynomials, sometimes it's more efficient to multiply out the terms before differentiating rather than directly applying the product rule.
- 🤔 Factoring the numerator of a quotient can sometimes simplify the derivative, but it's not always necessary or helpful, depending on the specific terms.
- 📊 Using graphing calculators or software like Desmos can help verify the equation of the tangent line and confirm the derivative calculations.
- ✅ When the denominator of a quotient is a single term, it can be beneficial to perform the division first before differentiating, which simplifies the application of the power rule.
- 🚀 Mastering the product and quotient rules, along with knowing when alternative methods are more efficient, is key to success in calculus.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is derivatives of products and quotients, focusing on rules for differentiating these types of functions without using the limit definition.
What is the product rule for differentiation?
-The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
How can you remember the product rule?
-A mnemonic to remember the product rule is to consider two functions, f and g, and recall it as 'f times g plus f times g derivative of the first and derivative of the second'.
What is the quotient rule for differentiation?
-The quotient rule states that the derivative of a quotient of two functions is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.
What is the advantage of using the product or quotient rule?
-The advantage of using the product or quotient rule is that it allows for the differentiation of products and quotients of functions without the need to use more complex limit definitions.
When is it beneficial to multiply out a product before differentiating?
-It is beneficial to multiply out a product before differentiating when dealing with polynomials, as it can simplify the differentiation process and reduce the number of steps required.
What is the derivative of the function f(x) = (2x^5 - 5x^3 + 1)(2x^4 + 3)?
-The derivative of the function f(x) = (2x^5 - 5x^3 + 1)(2x^4 + 3) is a polynomial expression resulting from applying the product rule and then combining like terms.
What is the slope of the tangent line to a function at a given point x=a?
-The slope of the tangent line to a function at a given point x=a is the value of the derivative of the function at that point, f'(a).
How can you find the equation of the tangent line to a function at a specific point?
-To find the equation of the tangent line, you first find the derivative of the function to get the slope (m) at the point of interest. Then, you find the y-coordinate (y1) by substituting the x-value (x1) into the original function. The equation of the tangent line is then given by y - y1 = m(x - x1).
Why is it sometimes better to divide before applying the quotient rule?
-It is sometimes better to divide before applying the quotient rule when the denominator is a single term, as it simplifies the expression and can make the differentiation process more straightforward.
What is the importance of combining like terms in the derivative expression?
-Combining like terms in the derivative expression is important for simplifying the derivative to its most straightforward form, which is essential for further calculations or analysis.
Outlines
😀 Introduction to Derivatives of Products and Quotients
The video begins with an introduction to the topic of derivatives of products and quotients. The presenter explains that they will cover differentiation rules for functions that are products or quotients of other functions, aiming to avoid using the limit definition. The focus is on the product rule, which is defined technically but can be simplified for easier understanding and application. The presenter also shares a mnemonic to help remember the product rule and demonstrates its application with an example involving polynomials.
📚 Applying the Product Rule and Simplifying Expressions
The presenter continues by applying the product rule to find the derivative of a function that is the product of two polynomials. They multiply the first function by the second function and add it to the first function multiplied by the derivative of the second function. After obtaining the derivative, they use algebraic skills to distribute, combine like terms, and simplify the expression. The presenter emphasizes the importance of being careful with algebra to avoid mistakes and suggests using different colors for better organization.
🔍 Deriving Tangent Line Slopes Using the Product Rule
The video script explores the application of the product rule to find the slope of a tangent line to a function at a specific point. The presenter demonstrates how to differentiate a function that is a product of two other functions and evaluates the derivative at a given x-value to find the slope of the tangent line. They also discuss the option to multiply out the function before differentiating as an alternative to using the product rule, which can sometimes be simpler.
🤔 Alternative Methods for Derivatives of Polynomials
The presenter discusses alternative methods for finding derivatives of polynomials, emphasizing that while the product rule is essential for some types of functions, it's not always necessary for polynomials. They show that by multiplying out the polynomials before differentiating, one can simplify the process. The presenter also demonstrates how to find the derivative of a single polynomial using the power rule after multiplying out the terms.
📉 Derivatives of Quotients and Simplifying Quotient Functions
The focus shifts to the quotient rule, which is necessary for differentiating a function that is a quotient of two other functions. The presenter explains the formal definition of the quotient rule and provides a simplified version for easier application. They work through an example, showing each step from taking the derivatives, applying the quotient rule, and simplifying the resulting expression. The presenter also highlights a potential option to factor the numerator but notes that it's not necessary in this case.
🧮 Equation of the Tangent Line Using the Quotient Rule
The presenter tackles a problem involving finding the equation of a tangent line to a function at a specific point using the quotient rule. They rewrite the function as a single fraction to simplify the differentiation process. After finding the derivative, they evaluate it at the given x-value to determine the slope of the tangent line. The presenter then finds the y-value corresponding to the x-value of the tangent line from the original function and uses these to write the equation of the tangent line, which is confirmed using Desmos.
📌 Special Considerations for Dividing Polynomials
The presenter addresses a special case where the denominator of a quotient function is a single term, suggesting that dividing first can simplify the differentiation process. They demonstrate how to simplify the quotient by dividing the terms and then applying the power rule to find the derivative. The presenter emphasizes that while the quotient rule is unavoidable in some cases, if the denominator is a single term, dividing first can make the problem significantly easier.
Mindmap
Keywords
💡Derivatives
💡Product Rule
💡Quotient Rule
💡Limit Definition
💡Polynomials
💡Algebraic Simplification
💡Distributing and Combining Like Terms
💡Tangent Line
💡Slope
💡Power Rule
💡Factoring
Highlights
Introduction to the topic of derivatives of products and quotients, emphasizing the importance of differentiation rules to simplify the process.
Explanation of the product rule for differentiation, including a simplified way to remember the formula.
Application of the product rule to a function that is the product of a fifth degree polynomial and a fourth degree polynomial.
Technique for committing the product rule to memory using the functions f and g, and the mnemonic for the quotient rule.
Demonstration of how to apply algebraic skills to combine like terms and simplify the derivative of a product of functions.
Differentiation of a function using the product rule, emphasizing the importance of careful algebra to avoid mistakes.
Strategy for differentiating a product of functions by first rewriting the function without a fraction, if possible, to simplify the process.
Introduction to the quotient rule for differentiation, which is essential for functions involving division.
Application of the quotient rule to differentiate a quotient of two functions, with an emphasis on organizing work to avoid errors.
Example of finding the slope of the tangent line to a function at a specific point using the derivative, which represents the slope.
Alternative method for differentiating a product of functions by first multiplying the functions together before differentiating.
Discussion on when to use the quotient rule versus when to simplify by dividing first, especially if the denominator is a single term.
Illustration of the quotient rule applied to a function with a more complex numerator and denominator, and the algebraic steps to simplify the derivative.
Use of Desmos to verify the equation of the tangent line at a specific point on a curve, demonstrating the practical application of differentiation.
Advice on keeping multiple options in mind when differentiating, such as using the quotient rule or dividing first, depending on the function's form.
Final problem demonstrating the quotient rule with a different denominator, showing how to simplify the derivative using algebraic techniques.
Emphasis on the importance of choosing the path of least resistance when differentiating, whether it's using the product or quotient rule or simplifying by multiplication or division first.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: