1.7 - The Chain Rule
TLDRThe video script offers an in-depth exploration of the chain rule in calculus, a fundamental concept for differentiating composite functions. It begins by explaining the concept of function composition, where one function's output becomes another function's input, creating a nested structure. The script emphasizes that composition is not commutative, meaning the order of functions matters, which is crucial for applying the chain rule accurately. The chain rule itself is introduced as a method to differentiate such nested functions, with the process involving finding the derivative of the outer function and multiplying it by the derivative of the inner function. The script walks through several examples to illustrate the application of the chain rule, including its use in conjunction with other differentiation rules like the product and quotient rules. The importance of simplifying expressions and factoring out common terms is also highlighted. The video concludes by noting that mastering the chain rule, along with other basic differentiation rules, equips one to handle a wide array of functions, with only a few special cases like exponential and logarithmic functions requiring additional rules.
Takeaways
- 📌 The chain rule is essential for differentiating composite functions, which are functions composed of two functions (an inner and an outer function).
- 🔍 Composing functions involves nesting one function inside another, while the chain rule allows us to differentiate such compositions by starting with the innermost function.
- ⚙️ The notation for function composition is f∘g (f composed with g), which is not commutative, meaning f∘g(x) is generally not the same as g∘f(x).
- 📈 To apply the chain rule, first find the derivatives of the inner and outer functions, then multiply the derivative of the outer function evaluated at the inner function by the derivative of the inner function.
- 🔢 The process of decomposition involves breaking down a complex function into simpler constituent functions to understand and differentiate it.
- ➗ Decomposition is the reverse of composition and helps in identifying the inner and outer functions of a complex function.
- 🔑 The order of operations is crucial in identifying the inner and outer functions and in evaluating the function step by step from the inside out.
- 🧩 Practicing function composition and decomposition helps in understanding how to apply the chain rule effectively.
- 🛠️ The chain rule can be combined with other derivative rules, such as the product rule and quotient rule, to handle more complex functions involving multiple operations.
- 📊 The power rule is a specific case of the chain rule where a function is raised to a power, and it's used to differentiate such expressions.
- ✅ Verifying the composition of decomposed functions by substituting the inner function into the outer function and checking if it matches the original complex function ensures the decomposition is correct.
Q & A
What is the chain rule in calculus?
-The chain rule is a fundamental theorem used for finding the derivatives of composite functions. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.
How does the concept of function composition relate to the chain rule?
-Function composition is when one function is nested inside another, serving as its input. The chain rule is essential for differentiating such composed functions, as it allows us to break down the complex function into simpler parts (inner and outer functions) and apply the derivative in a step-by-step manner.
Why is it important to start with the inner function when applying the chain rule?
-Starting with the inner function is crucial because it represents the first operation in the sequence of operations that define the composite function. The output of the inner function becomes the input for the outer function, and this sequential application helps in systematically finding the derivative.
What does it mean for a function to be commutative?
-A function or operation is commutative if the order in which the elements are combined does not affect the result. For example, addition and multiplication are commutative operations. However, function composition, as well as subtraction and division, are generally not commutative.
How can you tell if a function is an inner or outer function in a composition?
-In a function composition, the inner function is the one that is nested inside the other and is evaluated first. The outer function is the one that receives the output of the inner function as its input. To identify them, consider the order of operations and which function's output is being used as the input for the subsequent function.
What is the purpose of decomposing a function in calculus?
-Decomposition of a function allows us to break down a complex function into simpler, constituent functions, typically an inner and an outer function. This process is useful for applying the chain rule to find derivatives of composite functions and to better understand the structure of the function.
What is the general structure of the chain rule formula?
-The general structure of the chain rule formula is (d/dx [f(g(x))]) = f'(g(x)) * g'(x), where f is the outer function, g is the inner function, f' represents the derivative of the outer function, and g' represents the derivative of the inner function.
Why is it said that the chain rule involves a 'layering effect'?
-The chain rule involves a 'layering effect' because it requires finding the derivative of the outer function and then applying it to the inner function. This creates a layered process where the derivative of one function is used as part of the derivative of another, hence the term 'chain rule' reflecting the chaining together of these derivatives.
How does the chain rule relate to the process of simplifying derivatives?
-The chain rule is used to simplify the process of finding derivatives of composite functions by breaking them down into more manageable parts. It allows us to apply the derivative of the outer function to the result of the inner function, and then multiply by the derivative of the inner function, which simplifies the overall computation.
What is the extended power rule, and how does it relate to the chain rule?
-The extended power rule is a specific case of the chain rule where a function is raised to a power. It involves bringing down the exponent in front of the function and then decreasing the exponent by one, effectively applying the power rule in conjunction with the chain rule.
Can you provide an example of how the chain rule is applied within the product rule or quotient rule?
-Yes, in more complex scenarios, the chain rule can be applied within the product rule or quotient rule when differentiating functions. For instance, when differentiating a function that is a product of two other functions, one of which is a composite function itself, you would first use the chain rule to differentiate the composite part and then apply the product rule to combine the derivatives.
Outlines
😀 Understanding the Chain Rule and Function Composition
This paragraph introduces the chain rule, a fundamental concept in calculus for differentiating composite functions. It explains that composite functions are created by nesting one function inside another, and emphasizes the importance of the order of function composition, noting that it is not commutative. The paragraph also outlines how to represent function composition and how to approach finding derivatives of such composed functions using the chain rule.
📚 Function Composition Examples and Non-Commutativity
The second paragraph provides examples of function composition with two given functions, f(x) and g(x), defined as x to the fourth power and 2 plus x cubed, respectively. It demonstrates how to find the composed functions f composed with g of x and g composed with f of x, highlighting that these compositions are not necessarily the same unless under specific conditions. The paragraph reinforces the concept that composition is not a commutative operation.
🔍 Decomposing Functions into Simpler Components
The third paragraph discusses the process of decomposing a complex function into simpler, constituent functions. It explains that decomposition is the reverse of composition and is essential for differentiating complex functions using the chain rule. The paragraph guides through identifying inner and outer functions and emphasizes that the order of operations is crucial for correct decomposition.
🧩 Applying Decomposition to Complex Functions
In this paragraph, the process of decomposition is applied to more complex functions. It outlines how to break down layered operations into an outer function and an inner function, which can then be composed to reconstruct the original function. The importance of identifying the order of operations and applying the correct mathematical rules is emphasized to ensure accurate decomposition.
📈 Derivative of Composite Functions Using the Chain Rule
The fifth paragraph delves into the application of the chain rule for finding derivatives of composite functions. It explains that the chain rule involves differentiating the outer function with the inner function as the input and then multiplying by the derivative of the inner function. The paragraph provides a step-by-step guide on how to apply the chain rule, including substituting the inner function into the derivative of the outer function.
🌀 Simplifying the Derivative Expressions
The sixth paragraph focuses on simplifying the derivative expressions obtained from the chain rule. It discusses the potential for combining factors outside parentheses and the importance of not distributing across parentheses with exponents other than one. The paragraph emphasizes the goal of simplifying the derivative to its most manageable form without overcomplicating the expression.
🔢 Further Simplification and Factoring Derivatives
The seventh paragraph continues the theme of simplification, showcasing how to further factor out common terms from the derivative expressions. It demonstrates the process of identifying and factoring the greatest common factors, which can lead to a more streamlined and understandable derivative form. The importance of recognizing common factors and combining like terms is highlighted.
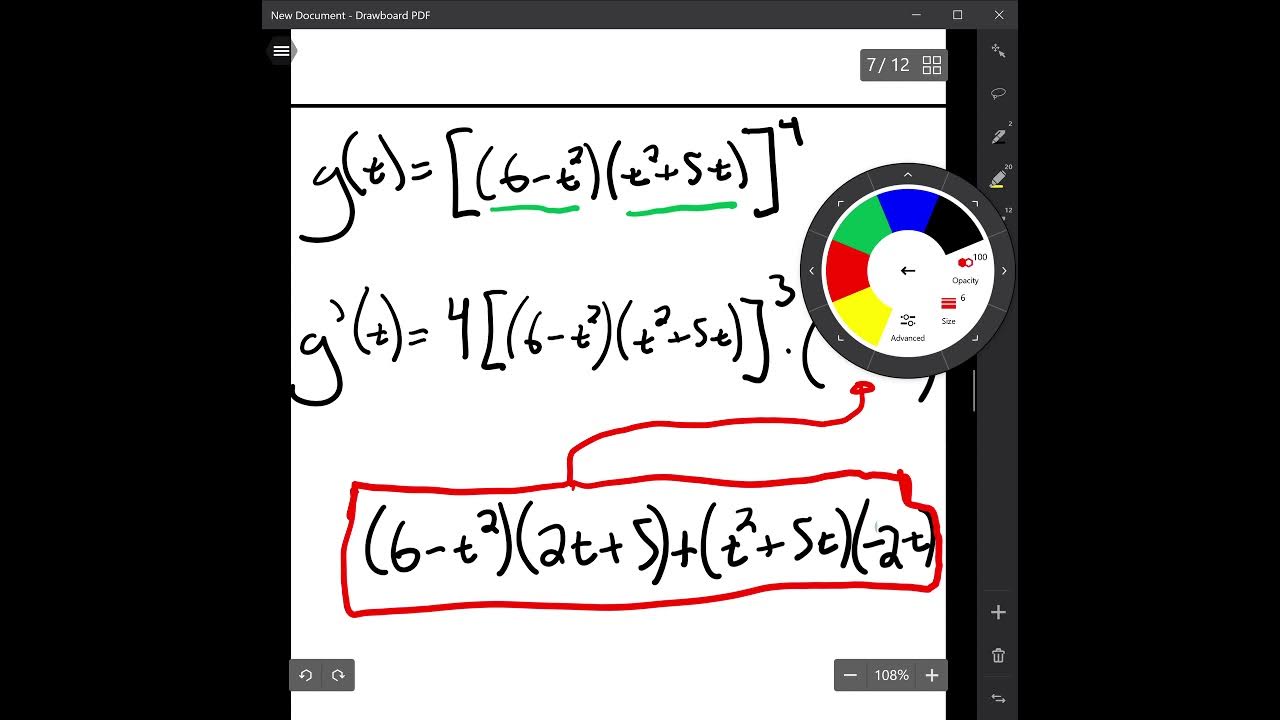
🤝 Chain Rule in Conjunction with Other Derivative Rules
The eighth paragraph explores the application of the chain rule in combination with other derivative rules, such as the product rule and quotient rule. It illustrates how to handle more complex functions that require nested applications of these rules. The paragraph emphasizes the need for a systematic approach to breaking down and differentiating each part of the function before recomposing the final derivative.
📖 Final Simplification and Mastering the Chain Rule
The final paragraph summarizes the process of simplifying derivatives obtained from the chain rule and other derivative rules. It reiterates the importance of factoring and combining like terms to achieve the most simplified form of the derivative. The paragraph concludes by emphasizing that mastering the chain rule, along with product, quotient, sum/difference, and power rules, equips one to differentiate a wide array of functions. It also notes that additional rules will be needed for specific operations like exponential and logarithmic functions.
Mindmap
Keywords
💡Chain Rule
💡Composite Function
💡Derivative
💡Power Rule
💡Product Rule
💡Quotient Rule
💡Exponent
💡Inner and Outer Functions
💡Decomposition
💡Order of Operations
💡Extended Power Rule
Highlights
The Chain Rule is introduced for handling complex functions that are compositions of simpler functions.
A composite function is explained as one function being nested inside another, creating a more complicated function.
The formal notation for function composition is introduced, emphasizing the difference between composition and multiplication symbols.
The Chain Rule is applicable for differentiating composite functions and requires starting with the inner function.
Order matters in function composition, which is not a commutative operation.
The process of decomposing a complex function into simpler constituent functions is demonstrated.
The importance of identifying the innermost and outermost operations when dealing with composite functions is emphasized.
Examples of function composition are provided, illustrating how different orders of composition result in different functions.
The concept of the Chain Rule is applied to various examples, showing how to differentiate complex functions step by step.
The Product Rule and Quotient Rule are combined with the Chain Rule for differentiating more complicated functions involving both products/quotients and compositions.
The process of simplifying derivatives through factoring and combining like terms is covered in detail.
The use of the Chain Rule in conjunction with other derivative rules is demonstrated for complex functions involving products, quotients, and compositions.
The concept of the extended power rule as a specific case of the Chain Rule is introduced.
The transcript provides a comprehensive guide on mastering the Chain Rule for differentiating a wide range of functions.
Special cases for exponential and logarithmic functions are mentioned as requiring additional derivative rules beyond the Chain Rule.
The Chain Rule is positioned as a fundamental tool for differentiating almost any function, once mastered.
The necessity of simplifying derivatives to their most preferred form after applying the Chain Rule and other derivative rules is highlighted.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: