Optimization: Minimum Average Cost

Sun Surfer Math
17 Mar 202206:54
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video guides viewers through the process of finding the minimum average cost using calculus. Initially, the presenter clarifies that the function given is a cost function, not an average cost function, and demonstrates how to derive the average cost function by dividing the cost function by the quantity, Q. The presenter then uses calculus to find the derivative, set it to zero, and solve for Q to find the optimal number of units for minimum average cost, which is determined to be 16 beach balls. The video concludes with a verification using the second derivative test, confirming that 16 units indeed result in a minimum average cost.

Takeaways
  • 📊 The cost function provided is not the average cost function; it needs to be derived by dividing the total cost by the quantity (q).
  • 🔍 There is only one independent variable, q, which means there's no need for a constraint equation in this scenario.
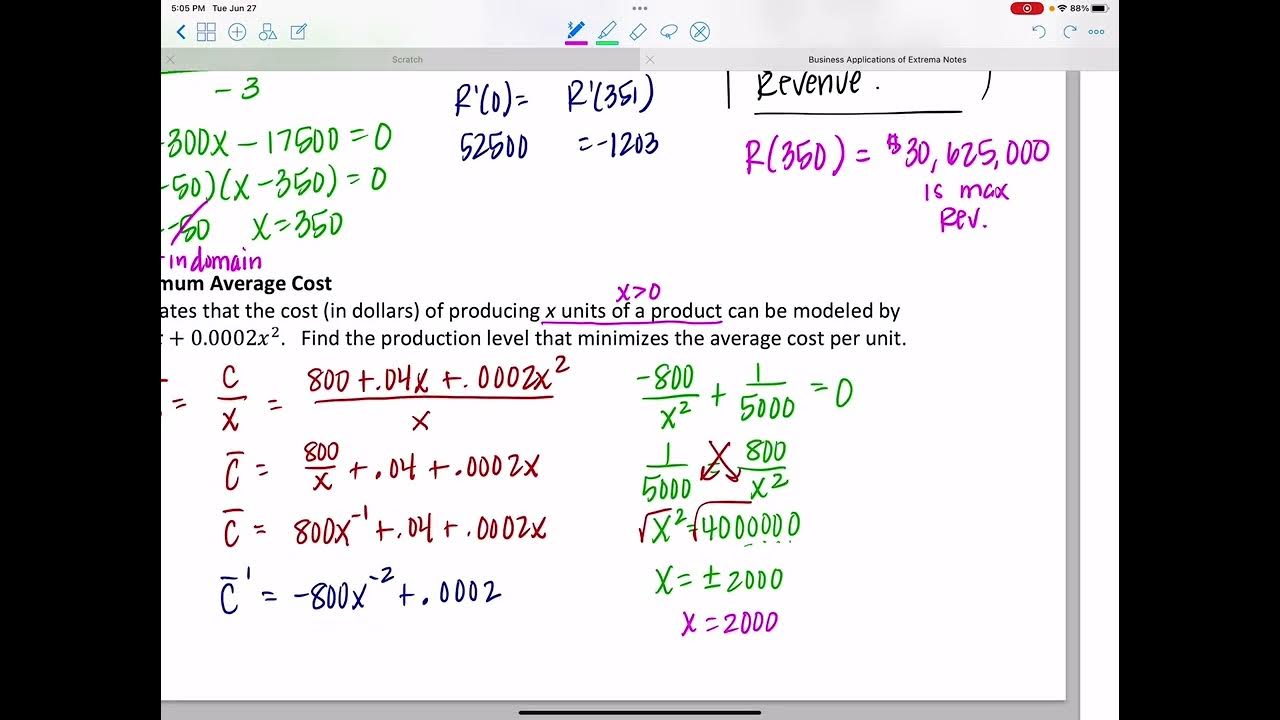
  • 🌟 The average cost function is obtained by dividing the cost function by the quantity, resulting in the formula 0.0q + 3 + 20q^(-1).
  • 📌 Calculus is used to find the minimum average cost by taking the derivative of the average cost function with respect to q.
  • 🧮 The derivative of the average cost function is calculated as 0.08 - 20q^(-2).
  • ⚖️ To find the minimum, set the derivative equal to zero and solve for q, which gives q^2 = 20/0.08.
  • 🔢 After solving, q is approximately equal to the square root of 250, which is around 15.8, but rounded to the nearest whole number, q = 16.
  • 🏁 The quantity of 16 beach balls is identified as the point that potentially gives the minimum average cost.
  • 🔍 To confirm if this is a minimum, the second derivative test is applied by finding the second derivative of the average cost function.
  • 📐 The second derivative is calculated as 40/q^3, and evaluating it at q=16 confirms that the value is positive, indicating a concave up curve and a relative minimum.
  • 📉 The second derivative test confirms that 16 is a relative minimum, which is the quantity that yields the minimum average cost.
  • 💡 To find the actual minimum average cost, substitute q with 16 back into the original average cost function.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is finding the minimum average cost using calculus.

  • Why is it important to differentiate between the cost function and the average cost function?

    -It's important because the cost function represents the total cost, while the average cost function represents the cost per unit, which is essential for finding the minimum average cost.

  • What is the independent variable in the given cost function?

    -The independent variable in the cost function is 'q', which represents the quantity of items.

  • How is the average cost function derived from the cost function?

    -The average cost function is derived by dividing the total cost function by the quantity 'q'.

  • What mathematical operation is used to find the minimum average cost?

    -Calculus is used, specifically by finding the derivative of the average cost function and setting it equal to zero.

  • How do you determine if the critical value found is a minimum or a maximum?

    -The second derivative test is used to determine if the critical value is a minimum or a maximum by evaluating the sign of the second derivative at that point.

  • What is the approximate quantity 'q' that gives the minimum average cost according to the video?

    -The approximate quantity 'q' that gives the minimum average cost is 16.

  • Why is the fractional quantity not acceptable when determining the number of beach balls?

    -Fractional quantities are not acceptable because you cannot have a fraction of a physical item like a beach ball.

  • What does it mean if the second derivative is positive at a critical point?

    -A positive second derivative at a critical point indicates that the function is concave up at that point, which means it is a relative minimum.

  • How do you verify that a critical point is indeed a minimum?

    -You verify that a critical point is a minimum by using the second derivative test and checking that the second derivative is positive at that point.

  • What is the final step to find the minimum average cost?

    -The final step is to evaluate the average cost function at the quantity 'q' that gives the minimum, which in this case is 16.

  • Why is it necessary to use the average cost function and not its derivative for the final evaluation?

    -The derivative is used to find the minimum point, but the actual cost is found using the original average cost function to ensure you get the cost per unit at the minimum point, not the rate of change.

Outlines
00:00
📊 Finding the Minimum Average Cost Function

This paragraph introduces the process of finding the minimum average cost by starting with a cost function. The presenter clarifies that the given function is not the average cost function itself, but rather the cost function from which the average cost function will be derived by dividing by the independent variable 'q'. The resulting average cost function is expressed as \( 0.0q + 3 + \frac{20}{q} \). To find the minimum average cost, calculus is employed by taking the derivative of the average cost function, which yields \( 0.08 - \frac{20}{q^2} \). Setting this derivative to zero and solving for 'q' leads to \( q^2 = \frac{20}{0.08} \), which simplifies to \( q = \sqrt{250} \approx 15.8 \). Since fractional quantities are not practical, 'q' is rounded up to the nearest whole number, 16. The presenter also discusses the need to verify whether this value of 'q' corresponds to a minimum average cost using the second derivative test, which involves finding \( \frac{40}{q^3} \) and evaluating it at 'q=16'.

05:01
🔍 Verifying the Minimum Average Cost with the Second Derivative Test

The second paragraph focuses on confirming that the calculated quantity 'q' indeed represents a minimum average cost using the second derivative test. The presenter calculates the second derivative of the average cost function, resulting in \( \frac{40}{q^3} \). By substituting 'q' with 16, the presenter determines that the second derivative is positive, indicating that the curve is concave up at this point, which confirms that 'q=16' is a relative minimum. This means that producing 16 units (in this case, beach balls) will yield the minimum average cost. To find the exact minimum average cost, the presenter instructs to evaluate the average cost function at 'q=16', which provides the minimum cost per unit.

Mindmap
Keywords
💡Minimum Average Cost
Minimum Average Cost refers to the lowest possible cost per unit that can be achieved when producing or providing a certain quantity of goods or services. In the video, the presenter is demonstrating how to calculate this by using a cost function and applying calculus to find the point where the average cost is minimized. This is a central concept of the video as it guides viewers through the process of optimization in a business or economic context.
💡Cost Function
A Cost Function is a mathematical representation that describes the relationship between the total cost of production and the quantity of goods or services produced. In the script, the presenter clarifies that the given function is not the average cost function but the total cost function, which needs to be manipulated to derive the average cost function. This is a fundamental concept as it forms the basis for the subsequent calculations.
💡Independent Variable
An Independent Variable is a variable that can be freely manipulated or changed in an experiment or calculation, and is not dependent on other variables. In the context of the video, 'q' represents the quantity of items produced, which is the sole independent variable. Understanding the role of the independent variable is crucial for the audience to follow the mathematical process of finding the minimum average cost.
💡Average Cost Function
The Average Cost Function is derived from the total cost function by dividing the total cost by the quantity of goods or services produced. It represents the cost per unit and is essential for determining the efficiency of production. In the video, the presenter shows how to derive this function from the given cost function by dividing it by 'q', which is then used to find the minimum average cost.
💡Derivative
In calculus, the Derivative of a function represents the rate at which the function's value changes with respect to changes in its independent variable. The presenter uses the concept of derivatives to find the point where the average cost function has its minimum value by setting the derivative equal to zero. This is a key step in the optimization process shown in the video.
💡Second Derivative Test
The Second Derivative Test is a method used in calculus to determine whether a critical point of a function is a relative maximum, relative minimum, or an inflection point. In the video, the presenter applies this test to verify that the calculated quantity 'q' indeed corresponds to a minimum average cost. The test involves finding the second derivative of the average cost function and evaluating it at the critical point.
💡Extrema
Extrema are points on a function where the derivative is zero or undefined, and they represent potential maximum or minimum values. In the context of the video, the presenter is interested in finding the minimum average cost, which corresponds to a relative minimum among the extrema. The concept of extrema is integral to the process of optimization being discussed.
💡Calculus
Calculus is a branch of mathematics that deals with rates of change and includes the study of differentiation and integration. In the video, calculus is used to find the minimum average cost by differentiating the average cost function and applying the second derivative test. It is the mathematical tool that enables the presenter to solve the optimization problem.
💡Optimization
Optimization is the process of finding the best solution or the most effective method for achieving a goal, often by maximizing or minimizing a particular function. In the video, the presenter is optimizing the production cost by finding the quantity 'q' that results in the minimum average cost. This is the overarching theme of the video, as it guides viewers through the steps of an optimization problem.
💡Critical Values
Critical Values are the values of the independent variable for which the derivative of a function is either zero or undefined. In the script, the presenter finds critical values by setting the derivative of the average cost function to zero. These values are potential candidates for minimum or maximum points and are essential for the optimization process.
💡Quantity 'q'
In the context of the video, 'q' is used to represent the quantity of a product, such as beach balls, being produced. The goal is to find the value of 'q' that results in the minimum average cost. The quantity 'q' is central to the video's narrative as it is the variable being optimized to achieve cost efficiency.
Highlights

The cost function is not the average cost function; it needs to be derived from it.

There is only one independent variable, q, in the cost function.

No need for a constraint equation due to a single independent variable.

The average cost function is obtained by dividing the cost function by q.

The average cost function formula is 0.0q + 3 + 20q^-1.

Calculus is used to find the minimum average cost by taking the derivative of the average cost function.

Derivative of the average cost function is 0.08 - 20q^-2.

Setting the derivative equal to zero and solving for q gives q^2 = 20/0.08.

q is approximately 15.8, which is rounded up to the nearest integer, 16.

Selling 16 beach balls is the quantity that should give the minimum average cost.

The second derivative test is used to verify if the found value is a minimum or a maximum.

The second derivative of the average cost function is 40/q^3.

Evaluating the second derivative at q=16 confirms a positive value, indicating a minimum.

A relative minimum is found at q=16, which is the quantity for minimum average cost.

The minimum average cost is found by evaluating the average cost function at q=16.

The final step is to plug in q=16 into the average cost function to get the minimum cost.

The video provides a step-by-step guide on finding the minimum average cost using calculus.

The process involves understanding the cost function, deriving the average cost function, and applying calculus to find the minimum.

Transcripts

Browse More Related Video

Marginal Revenue, Average Cost, Profit, Price & Demand Function - Calculus

Marginal Cost and Average Total Cost

Business Applications of Extrema

Marginal and Average Cost

Optimization Problem Examples

Business Calculus - Section 3.4 - Optimization and Elasticity of Demand

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Cost OptimizationCalculus ApplicationProduction EconomicsDerivative AnalysisSecond Derivative TestMinimum CostMathematical ExampleEconomic EfficiencyBusiness StrategyQuantitative AnalysisOptimization Techniques