Calculus 1 Lecture 2.2: Techniques of Differentiation (Finding Derivatives of Functions Easily)
TLDRThis comprehensive transcript delves into the intricacies of calculus, specifically focusing on differentiation techniques. It begins by establishing the foundational concept that the derivative of a constant is zero, a principle crucial for understanding the slope of horizontal lines. The instructor then explores the derivative as a measure of slope and introduces the limit definition of a derivative. The discussion progresses to the power rule for derivatives, illustrating how to find derivatives of polynomial and fractional functions efficiently. The application of these concepts is showcased through solving for points where a curve has a horizontal tangent, which corresponds to setting the first derivative equal to zero. The transcript further expands on higher-order derivatives, explaining the notation and the process of repeatedly differentiating a function. The importance of algebraic manipulation in preparing functions for differentiation is emphasized, particularly when dealing with complex expressions involving division. The material is presented in a manner that demystifies the often-intimidating subject of calculus, making it accessible to those new to the field while providing a solid foundation for further study.
Takeaways
- 📈 The slope of a constant horizontal line is always zero, which means the derivative of any constant is also zero.
- 🔑 Understanding that the derivative represents the slope of a curve, and by extension, the rate of change, is fundamental to calculus.
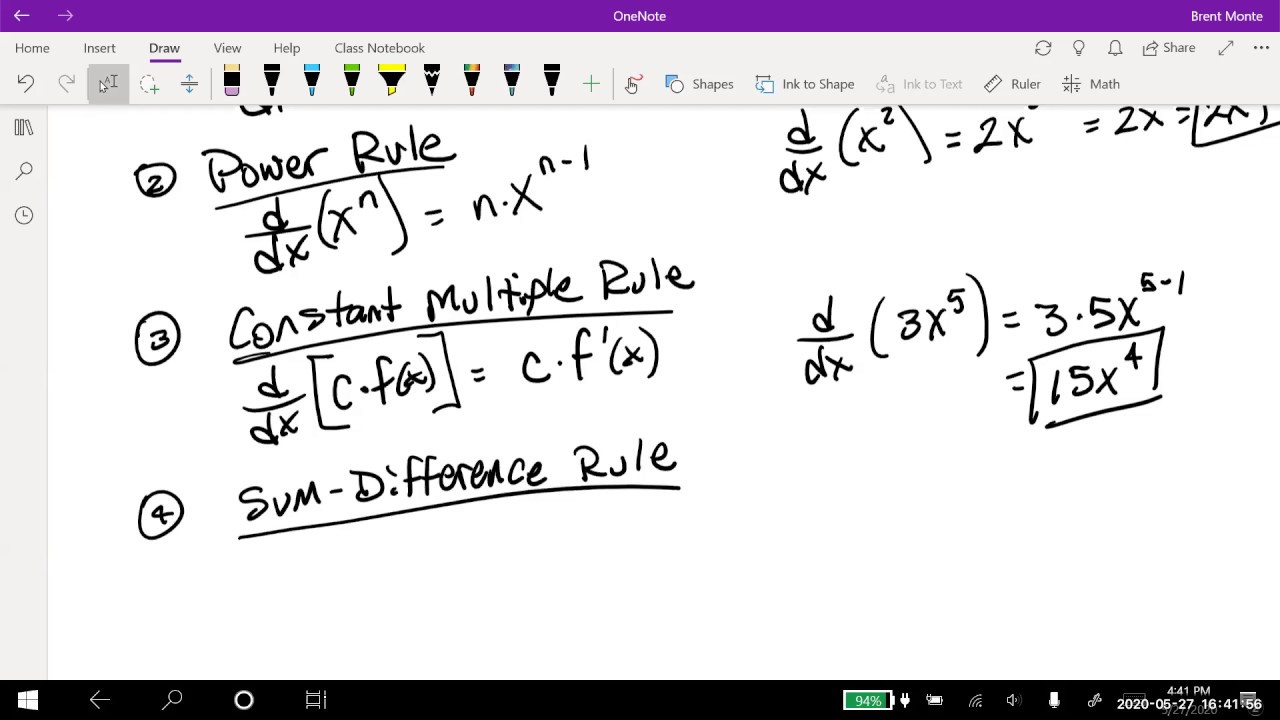
- 📚 The power rule for derivatives states that the derivative of X to the power of n is n times X to the power of n minus one (d/dx [x^n] = n * x^(n-1)).
- 📝 When dealing with constants multiplied by functions, you can factor out the constant from the derivative since the derivative of a constant is zero.
- 🔍 To find where a function has a horizontal tangent line, set the derivative equal to zero and solve for the variable, as horizontal tangents have a slope of zero.
- 🔢 For polynomial functions, taking successive derivatives will eventually lead to zero, as the degree of the polynomial decreases with each derivative.
- ➗ When dividing expressions with the same base, you subtract the exponents, which is crucial for simplifying fractions before taking derivatives.
- 🚫 You cannot directly take the derivative of a complex fraction or an expression connected by multiplication or division; it must be separated into individual terms first.
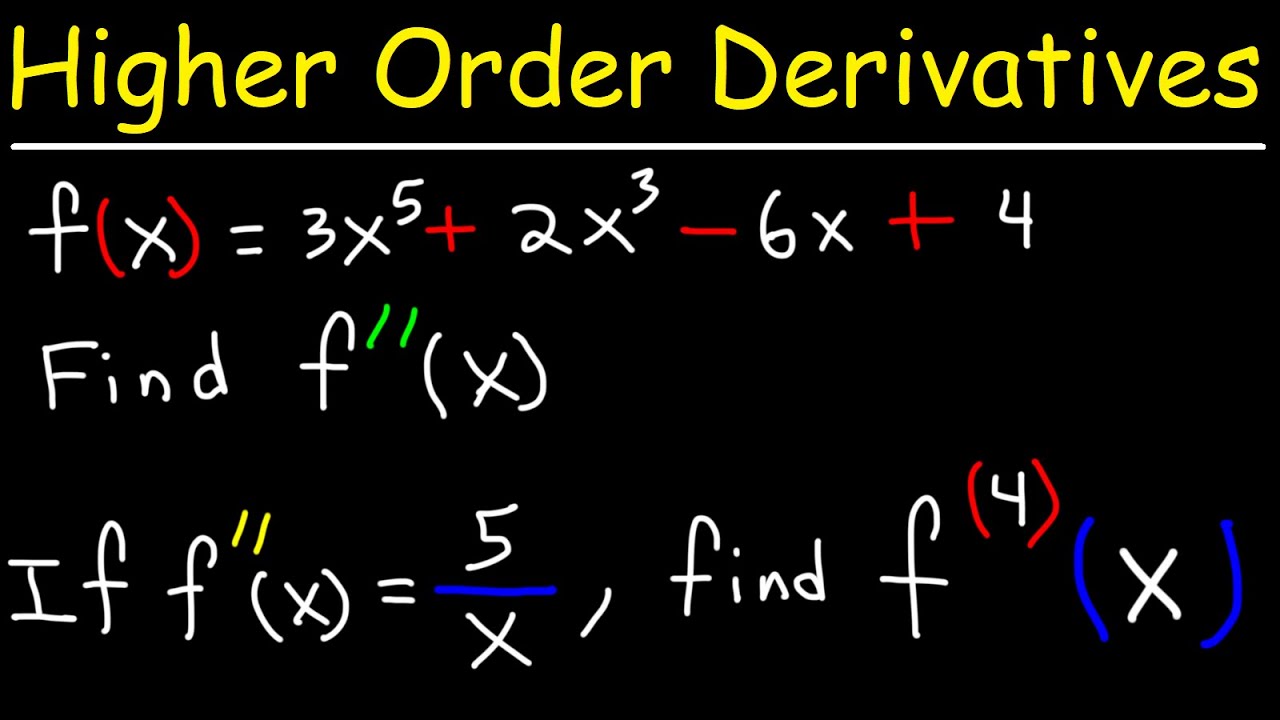
- 🔁 Higher-order derivatives, such as the second, third, or further, are found by taking the derivative multiple times, which can reveal important information about the function's behavior.
- 📌 The notation for derivatives varies, with 'F prime of X' or 'y prime' being common, and higher-order derivatives denoted by additional primes or subscripted numbers.
- 🧮 Knowledge of algebra is essential for calculus, as many calculus operations, such as simplifying expressions and working with exponents, are rooted in algebra.
Q & A
What is the slope of a horizontal line?
-The slope of a horizontal line is zero, as it does not rise or fall.
What is the derivative of a constant?
-The derivative of any constant is zero, regardless of the value of the constant.
What is the power rule for derivatives?
-The power rule for derivatives states that the derivative of X to the power of n is n times X to the power of (n - 1).
How can you find the slope of a curve at any point?
-You can find the slope of a curve at any point by taking the derivative of the curve's equation and then plugging in the x-value of the specific point.
What does it mean if a function has a horizontal tangent line?
-If a function has a horizontal tangent line, it means that the slope of the tangent line, and thus the derivative of the function at that point, is zero.
How can you find where a function has horizontal tangent lines?
-To find where a function has horizontal tangent lines, you set the derivative of the function equal to zero and solve for the variable.
What is the significance of finding the points where the derivative of a function is zero?
-Finding the points where the derivative is zero is significant because these points often correspond to local maxima, local minima, or points of inflection in the function.
What happens to the exponent when you take the derivative of a term with a fractional exponent?
-When you take the derivative of a term with a fractional exponent, you subtract 1 from the exponent.
How can you simplify a derivative expression that involves a fraction?
-You can simplify a derivative expression that involves a fraction by first simplifying the fraction itself, then applying the power rule to each term in the numerator and denominator separately.
What is the process of taking multiple derivatives of a function called?
-The process of taking multiple derivatives of a function is called finding higher-order derivatives.
Why is it important to know algebra well when studying calculus?
-Knowing algebra well is important in calculus because algebraic manipulation is often required to simplify expressions and apply calculus rules, such as the power rule.
Outlines
😀 Introduction to Derivatives of Constants
The paragraph begins with an introduction to the concept of derivatives, specifically focusing on the derivative of a constant. It explains that the slope of a horizontal line, which represents a constant value, is zero. The speaker emphasizes that the derivative of any constant is also zero, a fundamental principle in calculus. They provide several examples to illustrate this, such as the derivatives of the constants 3, -1, and π.
📚 Applying the Limit Process to Find Derivatives
This paragraph delves into the process of finding derivatives using limits. The speaker outlines a step-by-step method for differentiating the function f(x) = x^3. By substituting x with (x + h) and simplifying, the limit as h approaches zero is taken to find the derivative. The paragraph also touches on the concept of using shortcuts in calculus, such as the power rule for derivatives, which simplifies the process significantly.
🔍 Power Rule and Its Applications
The paragraph explains the power rule for derivatives, which allows for the simplification of derivative calculations. It demonstrates how to apply the power rule to various powers of x, including integer and fractional exponents. The speaker also discusses the derivative of x to the power of one and how it simplifies to 1, highlighting the relationship between derivatives and slopes of functions.
🧮 Derivatives of Functions with Variables and Constants
This section focuses on the process of differentiating functions that include both variables and constants. It explains that constants can be factored out of derivatives, as they do not affect the rate of change. The paragraph provides several examples, illustrating how to handle different types of functions, including those with negative exponents and square roots, using the power rule.
🔢 Derivatives of Polynomials and the Power Rule
The paragraph discusses the process of finding derivatives of polynomials using the power rule. It emphasizes that the power rule can be applied term by term for polynomials, allowing for the simplification of the derivative calculation. The speaker also explains how to handle constants within polynomials and how they can be factored out of the derivative.
🔁 Higher-Order Derivatives and Their Patterns
This paragraph introduces higher-order derivatives, which are derived by taking the derivative of a derivative. It explains that for polynomials, each subsequent derivative decreases the order of the polynomial by one until it eventually reaches zero. The speaker also notes that this pattern does not always hold for non-polynomial functions and provides an example to illustrate this.
🚫 Limitations of Derivative Rules for Connected Terms
The paragraph highlights the limitations of derivative rules when dealing with connected terms, such as those found in fractions or products that cannot be separated. It emphasizes that while terms can be separated by addition or subtraction, they cannot be separated by division or multiplication unless a constant is factored out. The speaker cautions against incorrectly applying derivative rules to such connected terms.
🧹 Simplifying Expressions for Derivatives
This section discusses the process of simplifying expressions before taking derivatives. It explains how to break down complex expressions into simpler components that can be differentiated using the power rule. The speaker demonstrates how to simplify fractions and how to combine terms with common bases by subtracting exponents, a fundamental algebraic concept.
📉 Finding the Slope of a Curve at Any Point
The final paragraph of the script focuses on using derivatives to find the slope of a curve at any given point. It explains that the derivative of a function represents the slope of the curve and that by finding the derivative, one can determine the slope at any point along the curve. The speaker also touches on the possibility of converting derivatives back into root form for clarity.
Mindmap
Keywords
💡Derivative
💡Constant
💡Slope
💡Limit
💡Binomial Expansion
💡Power Rule
💡Tangent Line
💡Polynomial
💡Higher-Order Derivatives
💡Newtonian Notation
💡Quotient Rule
Highlights
Derivative of a constant function is always zero, regardless of the constant's value.
The slope of a horizontal line is zero, which is why the derivative of a constant (horizontal line) is zero.
Derivatives can be found using the limit definition or by applying the power rule as a shortcut.
The power rule states that the derivative of x to the power of n is n times x to the power of n minus one.
Constants can be factored out of derivatives because they do not affect the rate of change.
The derivative of a function at a point gives the slope of the tangent line to the function at that point.
Horizontal tangent lines occur where the derivative of a function is zero, indicating a change from increasing to decreasing or vice versa.
Higher-order derivatives can be found by taking successive derivatives of a function.
The notation for higher-order derivatives includes primes (') for Newton's method or can use subscripts with dy/dx.
For polynomials, the nth derivative will eventually reach zero after n applications of the derivative.
Non-polynomial functions may not have their derivatives reach zero and can have derivatives of all orders.
When dealing with fractions, you can separate the terms and simplify each before taking the derivative.
Derivatives of terms with common bases can be simplified by subtracting exponents.
Quotients and products within a derivative require special handling and cannot be separated by simple addition or subtraction.
The process of finding derivatives involves both algebraic manipulation and application of the power rule.
Derivatives have practical applications in finding slopes of tangent lines and optimizing functions.
Understanding algebra is crucial for success in calculus, especially when dealing with fractions and exponents.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: