Logarithmic Equations
TLDRThis educational video script offers a detailed walkthrough on solving complex logarithmic equations. It begins by simplifying the equation log(x^2) = log(x^2) using logarithmic properties, such as moving the exponent to the front, resulting in 2*log(x). The script then guides viewers through the process of isolating variables, substitution with a new variable 'a', factoring, and applying the zero product property to find solutions. It also explains converting logarithmic forms to exponential forms and verifying solutions by substituting back into the original equation. The script further tackles a second example involving square roots and demonstrates similar steps to reach the solutions, emphasizing the importance of understanding logarithmic properties and algebraic manipulation for problem-solving.
Takeaways
- 📚 The script discusses solving logarithmic equations, starting with the equation \( \log(x^2) = \log(x^2) \).
- 🔍 It introduces a logarithmic property where \( \log_a(x^n) = n \cdot \log_a(x) \), and applies it to simplify \( \log(x^2) \) to \( 2 \log(x) \).
- ✏️ The next step is to isolate \( \log(x) \) by moving \( 2 \log(x) \) to the other side of the equation, resulting in \( \log(x^2) - 2 \log(x) = 0 \).
- 📐 The script suggests using substitution to simplify the equation, setting \( a = \log(x) \), which leads to \( a^2 - 2a = 0 \).
- 🔑 The greatest common factor (GCF) is factored out, reducing the equation to \( a(a - 2) = 0 \), leading to solutions \( a = 0 \) or \( a = 2 \).
- 📉 By setting \( a = 0 \), it is deduced that \( \log(x) = 0 \), and by setting \( a = 2 \), \( \log(x) = 2 \).
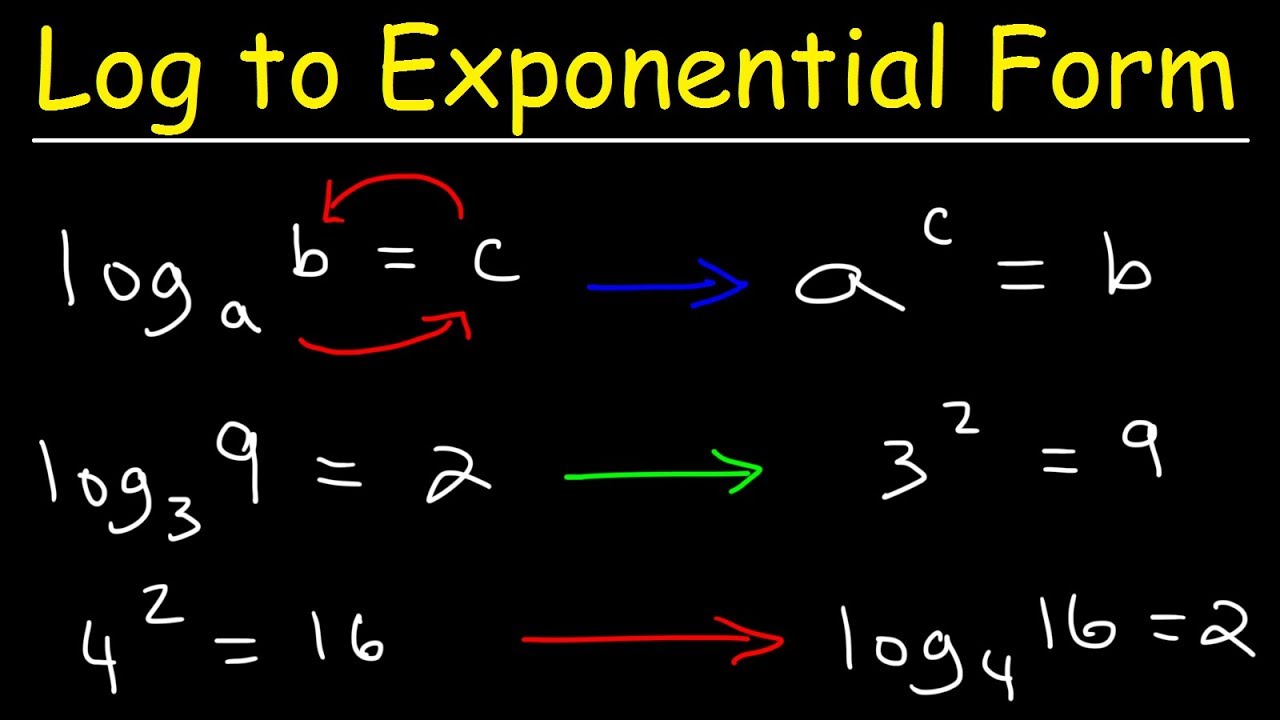
- 🔄 The script explains converting logarithmic solutions to exponential form, giving \( x = 10^0 \) which equals 1, and \( x = 10^2 \) which equals 100.
- 🔍 It verifies the solutions by plugging them back into the original equation, confirming that \( x = 1 \) and \( x = 100 \) are correct.
- 📘 The second part of the script tackles the equation \( \log(\sqrt{2x}) = \sqrt{\log(2x)} \), and it suggests rewriting the square root as a fractional exponent.
- 📚 The fractional exponent is eliminated by squaring both sides of the equation, leading to \( \frac{1}{4} \cdot a^2 - a = 0 \) after substitution.
- 📝 After multiplying by 4 to clear the fraction and factoring, the solutions are found to be \( a = 0 \) or \( a = 4 \), which correspond to \( x = \frac{1}{2} \) and \( x = 5000 \).
- 🔄 The script concludes by verifying the solutions for the second equation, confirming that both \( x = \frac{1}{2} \) and \( x = 5000 \) satisfy the original equation.
Q & A
What is the property of logarithms discussed in the video that allows us to simplify log x squared?
-The property discussed is that log a to the power of b is equal to b times log a. This allows us to move the exponent to the front, simplifying log x squared to 2 times log x.
How does the video suggest we should proceed after simplifying log x squared to 2 log x?
-The video suggests moving the 2 log x term to the right side of the equation, which results in log x squared minus 2 log x being set to zero.
What substitution technique is used in the video to solve the equation involving logarithms?
-The video uses the substitution technique where a is set equal to log x, which allows us to rewrite the equation in terms of a and simplify further.
How does the greatest common factor (GCF) come into play when solving the logarithmic equation in the video?
-After substitution, the GCF, which is 'a' in this case, is factored out to simplify the equation to a squared divided by a minus 2a divided by a, leading to a simplified equation of a minus two equals zero.
What is the zero product property mentioned in the video, and how is it used?
-The zero product property states that if a product of factors equals zero, then at least one of the factors must be zero. In the video, it is used to set each factor (a and a - 2) equal to zero to find the solutions for 'a'.
How does the video explain converting logarithmic equations to their exponential form?
-The video explains that if log base a of b equals c, then the exponential form is a raised to the power of c equals b. It also mentions that if no base is given, it is assumed to be base 10.
What are the two solutions for x found in the video using the properties of logarithms?
-The two solutions for x are x equals 1 and x equals 100. These are found by converting the logarithmic equations to their exponential forms and solving for x.
How does the video verify the correctness of the solutions for the logarithmic equation?
-The video verifies the solutions by plugging them back into the original equation and confirming that both sides of the equation are equal, thus proving the solutions are correct.
What is the second logarithmic equation problem presented in the video, and how does it differ from the first?
-The second problem is log square root 2x equals the square root of log 2x. It differs from the first in that it involves square roots of both the argument and the entire logarithm, requiring different manipulations to solve.
How does the video approach solving the second logarithmic equation involving square roots?
-The video suggests moving the fractional exponent to the front, squaring both sides of the equation to eliminate the square root, and then making a substitution to solve for x.
What are the two solutions for x found for the second logarithmic equation, and how are they verified?
-The two solutions for x are x equals 1/2 and x equals 5000. They are verified by plugging them back into the original equation and confirming that both sides of the equation are equal.
Outlines
📚 Solving Logarithmic Equations
This paragraph introduces the process of solving a logarithmic equation where log x squared equals log x squared. The presenter explains the properties of logarithms, particularly how to manipulate exponents within a logarithm, and suggests moving the exponent to the front to simplify the equation. The solution involves isolating log x, using substitution with a new variable 'a' set equal to log x, and then factoring out the greatest common factor (GCF) to solve for 'a'. The presenter also covers converting logarithmic forms to exponential forms, assuming base 10 when no base is specified, and provides two solutions: x equals 1 and x equals 100, verifying these solutions by substituting them back into the original equation.
🔍 Advanced Logarithmic Equations and Verification
The second paragraph delves into solving a more complex logarithmic equation involving square roots: log square root 2x equals the square root of log 2x. The presenter suggests moving the fractional exponent to the front and then squaring both sides of the equation to eliminate the fraction. Substitution is used again, this time with 'a' equal to log 2x, leading to a quadratic equation which is then factored and solved for 'a'. The solutions are x equals one half and x equals 5000. The presenter demonstrates the verification process by plugging these solutions back into the original equation, confirming their correctness through mathematical equivalence.
📘 Conclusion and Review of Logarithmic Problem-Solving Techniques
In the final paragraph, the presenter wraps up the discussion on solving difficult logarithmic equations. They summarize the methods used, including exponent manipulation, substitution, and converting between logarithmic and exponential forms. The presenter also emphasizes the importance of verifying solutions by substituting them back into the original equations. The solutions for the problems discussed are reiterated, and the presenter thanks the viewers for watching, encouraging them to apply these techniques to solve similar problems.
Mindmap
Keywords
💡Logarithm
💡Exponent
💡Logarithmic Property
💡Substitution
💡Greatest Common Factor (GCF)
💡Zero Product Property
💡Exponential Form
💡Base of a Logarithm
💡Equation
💡Verification
Highlights
Introduction to solving logarithmic equations by simplifying log x squared = log x squared.
Explanation of the logarithmic property where log a^n = n * log a.
Technique to move the exponent to the front in logarithmic equations.
Isolating log x by moving terms to the opposite side of the equation.
Substitution method using variable 'a' to represent log x.
Application of the zero product property to find solutions.
Conversion of logarithmic form to exponential form using base 10.
Derivation of two possible solutions for x: x = 1 and x = 100.
Verification of solutions by substituting back into the original equation.
Introduction to the second example involving square roots and logarithms.
Rewriting square roots as exponents and applying logarithmic properties.
Squaring both sides of the equation to eliminate fractional exponents.
Substitution of 'a' for log 2x to simplify the equation.
Factoring out the greatest common factor to solve for 'a'.
Finding two solutions: log 2x = 0 and log 2x = 4.
Conversion of these solutions into exponential form to find x values.
Derivation of x values: x = 0.5 and x = 5000.
Verification of the correctness of the solutions by plugging them back into the equation.
Conclusion summarizing the method to solve complex logarithmic equations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: