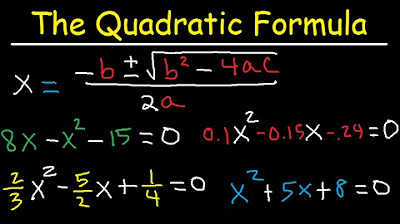Solving Polynomial Equations Using Goal Seek In Excel
TLDRThis tutorial video demonstrates how to solve various types of equations using Excel's Goal Seek feature. It covers linear, quadratic, and polynomial equations, showing step-by-step how to set up the equations in Excel and use Goal Seek to find the solutions. The video provides practical examples, including handling multiple solutions for quadratic equations and adjusting initial values to ensure accurate results. It's an informative guide for those looking to leverage Excel for solving complex mathematical problems.
Takeaways
- 📘 The video is a tutorial on solving equations using Excel's Goal Seek feature.
- 🔍 It covers solving linear, quadratic, and polynomial equations with examples.
- 📈 The process begins by writing the equation in column A and setting up the corresponding Excel formula in column D.
- 📝 For linear equations, Excel calculates 'y' values based on different 'x' inputs in column C.
- 🎯 The Goal Seek tool is used to find the exact 'x' value that makes the equation true, such as setting 'y' to 245 in the example.
- 📊 The quadratic equation example demonstrates how to set up and solve equations like 4x^2 - 7x = 200 using Goal Seek.
- 🔑 The video explains that sometimes quadratic equations have two solutions, and Goal Seek can find both by adjusting initial 'x' values.
- 🤔 It shows that for equations with multiple solutions, choosing a starting 'x' value closer to one of the solutions can help find it using Goal Seek.
- 📚 The tutorial also addresses how to solve polynomial equations, such as 3x^3 + 5x^2 - 9x - 9086 = 0, in Excel.
- 👉 The video suggests using trial and error with different 'x' values to get closer to the desired 'y' value when solving polynomial equations.
- 👍 The final takeaway is that the Goal Seek feature in Excel is a powerful tool for solving a variety of equations, with some manual adjustments needed for complex cases.
Q & A
What is the main topic of the video?
-The main topic of the video is how to solve equations using the goal seek feature in Excel.
What types of equations are covered in the video?
-The video covers linear equations, quadratic equations, and polynomial equations.
How does the video guide the viewer to use Excel for solving equations?
-The video provides step-by-step instructions on setting up the equations in Excel, using cell references to represent variables, and utilizing the goal seek feature to find the solution.
What is the purpose of labeling Column C as 'x values' and Column D as 'equation'?
-Labeling Columns C and D helps to organize the data and makes it clear which column represents the variable x and which represents the equation to be solved.
How does the video demonstrate solving a linear equation in Excel?
-The video demonstrates by setting up a linear equation (12x + 17 = 245) in cells, using cell references for x, and then using the goal seek feature to find the value of x that results in y equaling 245.
What is the significance of using cell references instead of actual numbers in the equation setup?
-Using cell references allows Excel to dynamically calculate the equation based on the value in the referenced cell, making it easier to find the solution for different x values.
How does the video handle the solution of a quadratic equation in Excel?
-The video shows how to set up a quadratic equation in Excel, using cell references for x, and then using the goal seek feature to find the x value that results in the equation equaling the target value.
What is the issue faced when trying to use the goal seek feature with a polynomial equation set to zero?
-The issue is that Excel might not converge to the correct solution when the target value is set to zero, so a close value to the actual answer is used instead.
How can the goal seek feature be used to find multiple solutions to an equation?
-By adjusting the starting x value closer to one of the known solutions and using the goal seek feature, Excel can provide the answer closest to that x value.
What is the final example in the video about?
-The final example demonstrates solving a fourth-degree polynomial equation using the goal seek feature in Excel, highlighting the process of finding multiple solutions.
Why might the goal seek feature give an approximate solution rather than an exact one?
-The goal seek feature might give an approximate solution due to the nature of numerical methods used by Excel, especially when dealing with equations that have multiple solutions or complex behaviors.
Outlines
📊 Solving Linear Equations with Excel's Goal Seek
This paragraph introduces the process of solving equations using Excel's goal seek feature. It begins with a linear equation example, 12x + 17 = 245. The speaker demonstrates how to set up the equation in Excel by labeling columns for x values and the equation itself. The equation is entered as '=12*C2+17', where C2 is the cell containing the x value. By changing the value in C2, different y values are calculated. The goal seek feature is then used to find the exact x value that results in a y value of 245. The process involves highlighting the y value cell, navigating to the 'Data' tab, selecting 'What-If Analysis', and then 'Goal Seek'. The set cell is directed to achieve a value of 245 by adjusting cell C2. The result, x = 19, is highlighted as the solution to the linear equation.
📈 Using Goal Seek for Quadratic Equations
The second paragraph explains how to solve quadratic equations using the goal seek feature in Excel. The example given is 4x^2 - 7x = 200. The equation is set up in Excel by replacing x with a cell reference (C5), resulting in '=4*C5^2 - 7*C5'. By plugging in different x values, the y values are calculated and observed. The goal seek feature is utilized to find the x value that results in y = 200. The process is similar to the linear equation, with the set cell directed to achieve a value of 200 by adjusting cell C5. The solution provided is x ≈ 8.0001, which can be rounded to 8. The paragraph also discusses an example with two possible solutions, x^2 - 3x - 40 = 0, and explains how to use goal seek to find both x = -5 and x = 8 by adjusting the initial x value in the set cell.
🔍 Advanced Goal Seeking with Polynomial Equations
The third paragraph delves into solving more complex polynomial equations using goal seek. The example equation is 3x^3 + 5x^2 - 9x - 9086 = 0. The equation is entered into Excel with x replaced by cell reference C11, resulting in '=3*C11^3 + 5*C11^2 - 9*C11 - 9086'. The goal seek feature is used to find an x value that results in y = 0. However, the initial attempt does not yield the target value of zero, suggesting that the starting value needs adjustment. By inputting a value closer to the expected solution, such as 10 or 20, the goal seek feature provides a more accurate result. The paragraph highlights the importance of selecting a starting value that is close to the actual solution to ensure the accuracy of the goal seek feature.
📚 Final Examples and Tips for Goal Seeking
The final paragraph provides additional examples of using the goal seek feature to solve equations, emphasizing the potential for multiple solutions and the importance of selecting appropriate starting values. The first example involves an equation with two solutions between 1 and 2, and another between 10 and 25. The speaker demonstrates how to use goal seek to find these solutions by adjusting the x value in cell C13 and setting the equation to zero. The solutions found are approximately x = 1.8438 and x ≈ 17. The paragraph concludes with a summary of how to use the goal seek feature in Excel to solve equations effectively, offering thanks to the viewers for watching the video.
Mindmap
Keywords
💡Goal Seek
💡Linear Equation
💡Quadratic Equation
💡Polynomial Equation
💡Excel
💡Variable
💡Equation
💡What-If Analysis
💡Cell Reference
💡Solution
Highlights
Introduction to using the goal seek feature in Excel to solve various equations.
Demonstration of solving a linear equation (12x + 17 = 245) using Excel.
Explanation of labeling columns for x values and equations in Excel.
Using cell references to dynamically calculate y values based on x inputs.
Utilizing the goal seek feature to find the exact x value that results in a y value of 245.
Highlighting the answer with a color to emphasize the solution.
Moving on to solve a quadratic equation (4x^2 - 7x = 200) in Excel.
Process of replacing x with cell references in the quadratic equation.
Using goal seek to find the x value that makes the quadratic equation equal to 200.
Dealing with a quadratic equation that has two solutions.
Approach to finding both solutions using goal seek by adjusting initial x values.
Solving a polynomial equation (3x^3 + 5x^2 - 9x - 9086 = 0) with Excel.
Method to replace x variables with cell references in a polynomial equation.
Challenges faced when using goal seek with a polynomial equation and adjusting the target value.
Final example of solving another polynomial equation and finding multiple solutions.
Strategy for narrowing down the range to find the second solution using goal seek.
Conclusion summarizing the use of the goal seek feature to solve equations in Excel.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: