Solving Exponential Equations In Quadratic Form - Using Logarithms, With e

The Organic Chemistry Tutor
16 Jan 201711:59
EducationalLearning
32 Likes 10 Comments

TLDRThis video tutorial delves into solving exponential equations in quadratic form. It illustrates the process through examples, starting with the equation e^(2x) - 5e^x + 6 = 0. The method involves factoring by substitution, setting a variable 'a' equal to e^x, and then solving the resulting trinomial equation. The video demonstrates finding the values of 'a' and subsequently solving for 'x' using natural logarithms. It emphasizes that e^x can never be negative, eliminating certain solutions. Additional examples are provided, including e^(2x) - 3e^x - 28 = 0 and e^(4x) - 14e^(2x) + 48 = 0, with solutions found by applying the same technique. The video concludes by noting that taking square roots of both sides can introduce extraneous solutions, but these are typically discarded due to the nature of exponential functions. The tutorial is both informative and engaging, offering a clear understanding of solving exponential equations.

Takeaways
  • 📚 The video focuses on solving exponential equations in quadratic form.
  • 🔍 The example equation e^(2x) - 5e^x + 6 = 0 is used to demonstrate the solving process.
  • 📝 Factoring and substitution are key techniques used to solve the equation, with 'a' substituting e^x.
  • 🔢 The numbers that multiply to the constant term and add up to the middle coefficient are identified to factor the trinomial.
  • 📉 Setting each factor equal to zero allows solving for 'a', which is then substituted back to find e^x.
  • 📚 The natural logarithm is used to isolate 'x' by taking ln on both sides of the equation.
  • 🚫 It's emphasized that e^x cannot be negative, so equations where e^x equals a negative number have no solution.
  • 🔄 The process is repeated with different equations to demonstrate the consistency of the method.
  • 📉 The video also covers the case where e^(2x) is set equal to different positive numbers and how to solve for 'x'.
  • 🔢 The solutions involve taking the natural logarithm and manipulating the exponent to solve for 'x'.
  • 📝 The video concludes with a reminder that all methods lead to the same solutions, even when using square roots.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is solving exponential equations in quadratic form.

  • What is the first example equation given in the video?

    -The first example equation is e^(2x) - 5e^x + 6 = 0.

  • What substitution is used to simplify the first example equation?

    -The substitution used is to let 'a' be equal to e^x, which simplifies e^(2x) to a^2.

  • What is the trinomial obtained after the substitution in the first example?

    -The trinomial obtained is a^2 - 5a + 6 = 0.

  • How do you find the factors of the trinomial a^2 - 5a + 6?

    -You find the factors by looking for two numbers that multiply to 6 and add up to -5, which are -2 and -3.

  • What are the solutions for 'a' in the first example?

    -The solutions for 'a' are a = 2 and a = 3.

  • How do you find the value of x when e^x = 2?

    -You find the value of x by taking the natural log of both sides, resulting in x = ln(2).

  • What is the second example equation provided in the video?

    -The second example equation is e^(2x) - 3e^x - 28 = 0.

  • Why is e^x never equal to a negative number?

    -e^x is never equal to a negative number because the exponential function e^x is always positive and never crosses the x-axis.

  • What is the process to solve e^(2x) = 8?

    -The process involves taking the natural log of both sides and then dividing by 2, resulting in x = (1/2)ln(8).

  • What are the solutions for x in the equation e^(4x) - 14e^(2x) + 48 = 0?

    -The solutions for x are x = (1/2)ln(8) and x = (1/2)ln(6).

  • Why can't we use the square root method for e^(2x) = 8 to find additional solutions?

    -We can't use the square root method because it would lead to e^x = -√8, which is not possible since e^x can never be negative.

Outlines
00:00
🧮 Solving Exponential Equations Using Substitution

This paragraph explains how to solve exponential equations in quadratic form using substitution. The example equation \( e^{2x} - 5e^x + 6 = 0 \) is given, and the substitution \( a = e^x \) is used to transform the equation into a quadratic \( a^2 - 5a + 6 = 0 \). Factoring the quadratic leads to solutions for \( a \), which are then converted back to solve for \( x \) by taking the natural logarithm. The solutions \( x = \ln 2 \) and \( x = \ln 3 \) are derived.

05:02
🔍 Example of Exponential Equation with No Solution

This paragraph provides another example of solving exponential equations: \( e^{2x} - 3e^x - 28 = 0 \). Using the substitution \( a = e^x \), the equation is transformed into \( a^2 - 3a - 28 = 0 \). Factoring leads to solutions \( a = -4 \) and \( a = 7 \). The equation \( e^x = 7 \) is solved to find \( x = \ln 7 \), but \( e^x = -4 \) has no solution because the exponential function cannot equal a negative number. This illustrates that exponential functions can never be negative.

10:04
📊 Final Example and Additional Solution Method

In this paragraph, a more complex exponential equation \( e^{4x} - 14e^{2x} + 48 = 0 \) is solved using substitution. Setting \( a = e^{2x} \) transforms the equation to \( a^2 - 14a + 48 = 0 \), which is then factored to find \( a = 8 \) and \( a = 6 \). Solving \( e^{2x} = 8 \) and \( e^{2x} = 6 \) yields solutions \( x = \frac{\ln 8}{2} \) and \( x = \frac{\ln 6}{2} \). The paragraph also explores using the square root to find \( e^x = \pm \sqrt{8} \), concluding that only the positive root is valid, reinforcing that exponential functions cannot be negative.

Mindmap
Keywords
💡Exponential Equations
Exponential equations are mathematical expressions involving exponential functions, where the variable is in the exponent. In the context of the video, the focus is on solving exponential equations that take on a quadratic form, such as 'e^(2x) - 5e^x + 6 = 0'. The video demonstrates methods to solve these equations by transforming them into a more familiar algebraic form and then applying factoring techniques.
💡Quadratic Form
A quadratic form in the context of the video refers to an exponential equation that resembles the standard quadratic equation 'ax^2 + bx + c = 0'. The script uses the substitution method to transform the exponential equation into a quadratic form, making it easier to solve by factoring or using the quadratic formula.
💡Factoring
Factoring is a mathematical technique used to break down a polynomial into a product of its factors. In the video, factoring is applied to the transformed quadratic form of the exponential equation to find the values of 'a', which represents 'e^x'. The script demonstrates how to find two numbers that multiply to the constant term and add up to the middle coefficient.
💡Substitution
Substitution is a method of replacing a complex expression with a simpler variable to make an equation easier to solve. In the script, 'a' is substituted for 'e^x', allowing the exponential equation to be rewritten in terms of 'a', which simplifies the process of solving for 'x'.
💡Natural Logarithm
The natural logarithm, often denoted as 'ln', is the logarithm to the base 'e', where 'e' is the mathematical constant approximately equal to 2.71828. The script uses the natural logarithm to solve for 'x' after finding the values of 'a'. It involves taking the natural log of both sides of the equation to isolate 'x'.
💡Leading Coefficient
The leading coefficient is the coefficient of the term with the highest power in a polynomial. In the video, the leading coefficient is '1' in the trinomial 'a^2 - 5a + 6 = 0', which is a key detail because it simplifies the factoring process.
💡Middle Coefficient
The middle coefficient in a quadratic equation is the coefficient of the middle term. In the script, it refers to the coefficient of 'a' in the equation 'a^2 - 5a + 6 = 0'. The video explains how to find two numbers that add up to this middle coefficient to help in factoring the quadratic form.
💡Constant Term
The constant term in a quadratic equation is the term without a variable, usually 'c' in 'ax^2 + bx + c = 0'. In the video, the constant term is '6' in the equation 'a^2 - 5a + 6 = 0', and it is crucial for determining the correct pair of numbers to factor the equation.
💡Horizontal Asymptote
A horizontal asymptote is a horizontal line that a function approaches as its input (or the variable) goes towards infinity or negative infinity. The script mentions that the exponential function 'e^x' has a horizontal asymptote at 'y = 0', indicating that it never touches or goes below this line, thus it can never be negative.
💡Natural Logarithm Properties
The properties of the natural logarithm allow for manipulation of the equation to isolate the variable. In the script, the property that 'ln(e^x) = x * ln(e)' is used, where 'ln(e)' equals '1', thus simplifying to 'x'. This property is essential for solving the exponential equations presented in the video.
💡Square Root
The square root operation is used to find a value that, when multiplied by itself, gives the original number. In the video, the square root of 'e^(2x)' is taken to transform the equation into 'e^x', which is then solved using natural logarithms. The script also mentions that taking the square root can introduce extraneous solutions that must be checked for validity.
Highlights

Introduction to solving exponential equations in quadratic form.

Example equation: e^(2x) - 5e^x + 6 = 0.

Using substitution with a = e^x to simplify the equation.

Factoring the resulting trinomial equation a^2 - 5a + 6 = 0.

Finding factors that multiply to 6 and add to -5: -2 and -3.

Setting each factor equal to zero to find values of a.

Solving for x when a = e^x: x = ln(2) and x = ln(3).

Demonstration of using natural log to solve for x.

New example equation: e^(2x) - 3e^x - 28 = 0.

Factoring the equation a^2 - 3a - 28 = 0.

Identifying factors of -28 that add up to -3: -4 and 7.

Realization that e^x cannot equal a negative number.

Explanation of the properties of exponential functions.

Third example equation: e^(4x) - 14e^(2x) + 48 = 0.

Using substitution with a = e^(2x) to form a^2 - 14a + 48 = 0.

Finding factors of 48 that add up to -14: -8 and -6.

Solving for x when e^(2x) = 8 and e^(2x) = 6.

Using natural log to solve for x in the equation e^(2x) = 8.

Solving for x in the equation e^(2x) = 6 and finding x = (1/2)ln(6).

Exploring alternative solutions involving square roots.

Clarification that e^x cannot be negative, eliminating ln(-4).

Final solutions for the equation: x = (1/2)ln(8) and x = (1/2)ln(6).

Transcripts

Browse More Related Video

How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course

Solving Exponential Equations Using Logarithms & The Quadratic Formula

Solve by Completing the Square: Step-by-Step Technique

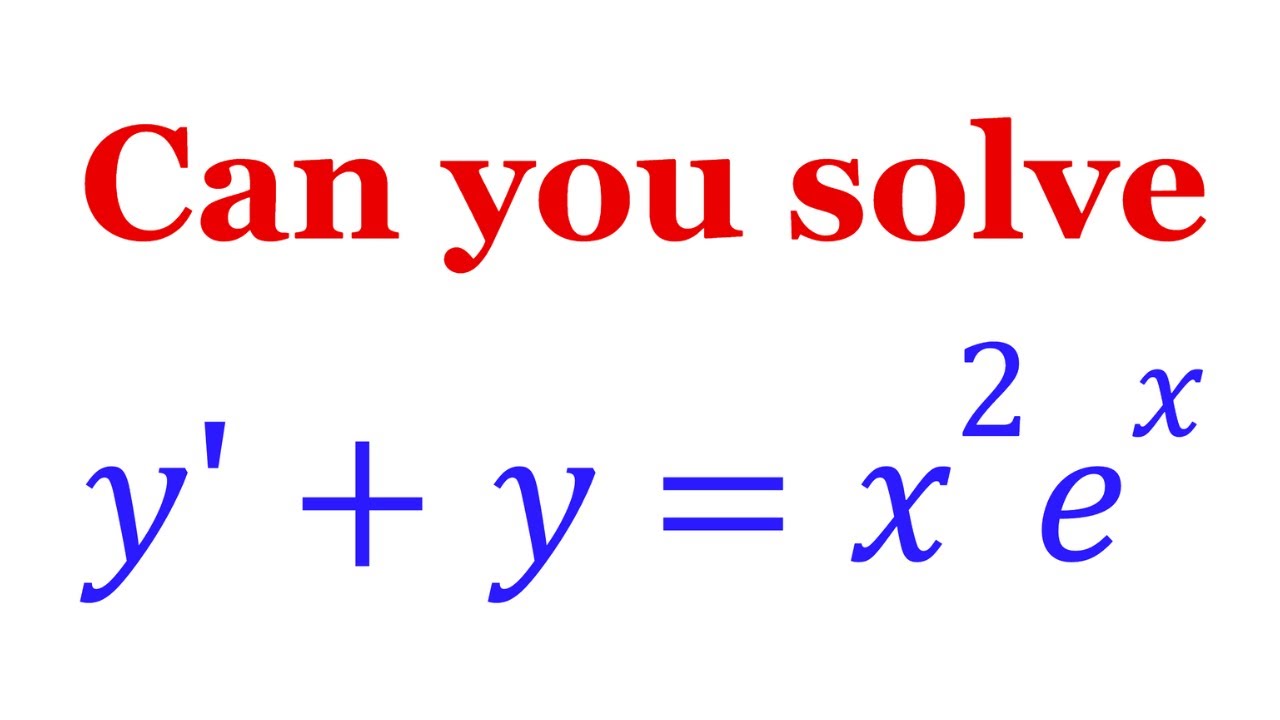
Let's Solve An Interesting Differential Equation

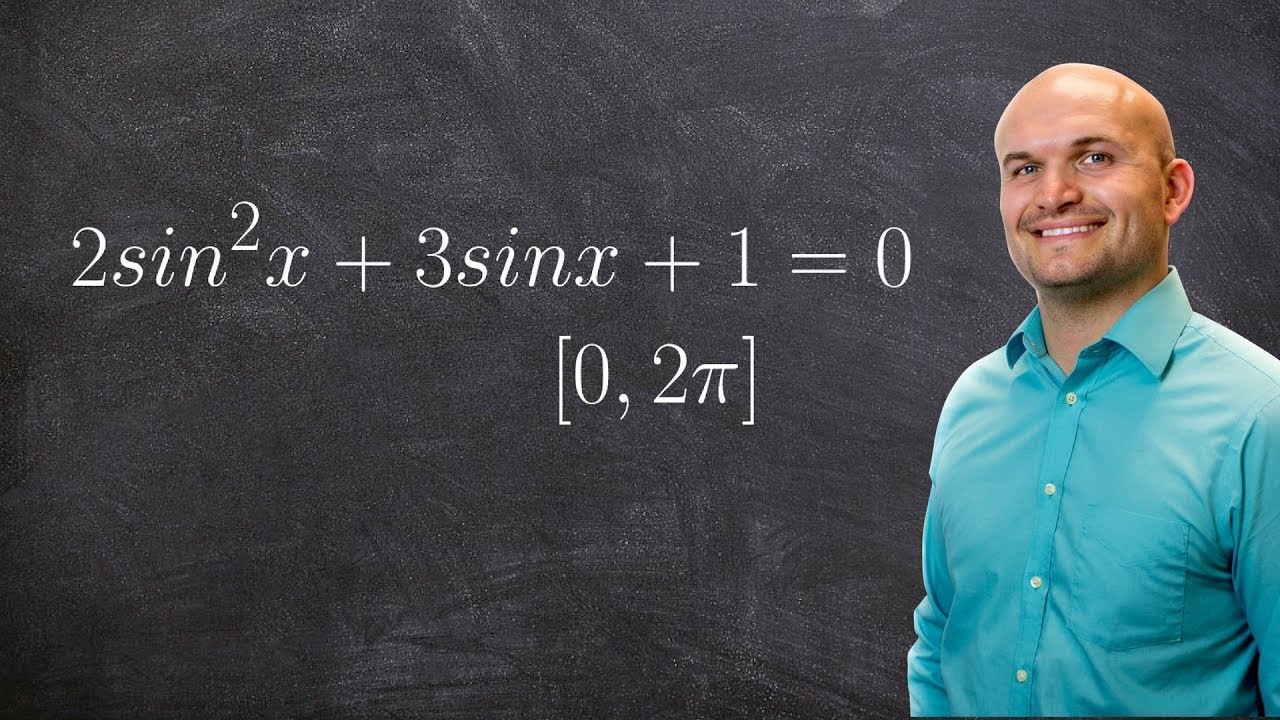
Solving a trigonometric equation by factoring

Derivatives of Exponential Functions

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Exponential EquationsQuadratic FormMathematicsEducational VideoSolving TechniquesFactorizationSubstitutionNatural LogarithmAlgebraProblem Solving