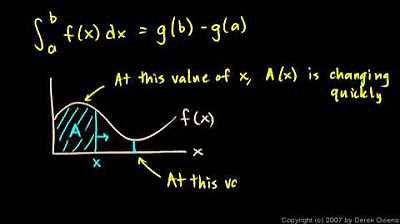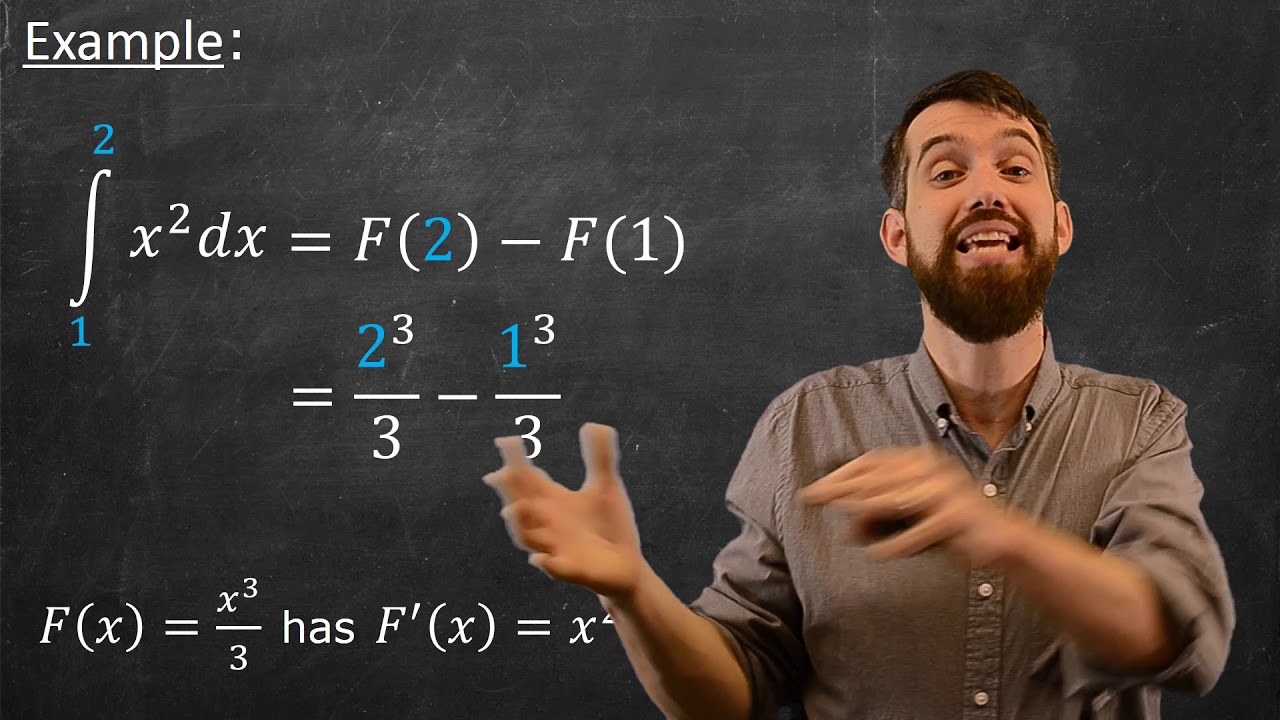An Intuitive Understanding of the Fundamental Theorem of Calculus
TLDRThe video script delves into the fundamental theorem of calculus, aiming to demystify why it works. It begins by reminding viewers that the area under a curve, represented by the integral from 'a' to 'b' of f(x)dx, can be found by evaluating the antiderivative G(x) at 'b' and 'a', then subtracting the two. The presenter challenges the audience to consider how one might find the area of a two-dimensional shape, hinting at multiplying a certain value by the width of the shape to get the area. The video then explores the concept of averaging an infinite number of values, specifically slopes, to find the average rate of change between two points. By finding the antiderivative of the function f(x), which is G(x), and evaluating it at 'b' and 'a', the presenter shows that the average value of the function over the interval can be found. This average value, when multiplied by the width of the interval, equals the area under the curve. The script concludes by illustrating that the fundamental theorem of calculus is a natural extension of these concepts, providing a clear and logical explanation for why evaluating the antiderivative at two points gives the exact area under the curve.
Takeaways
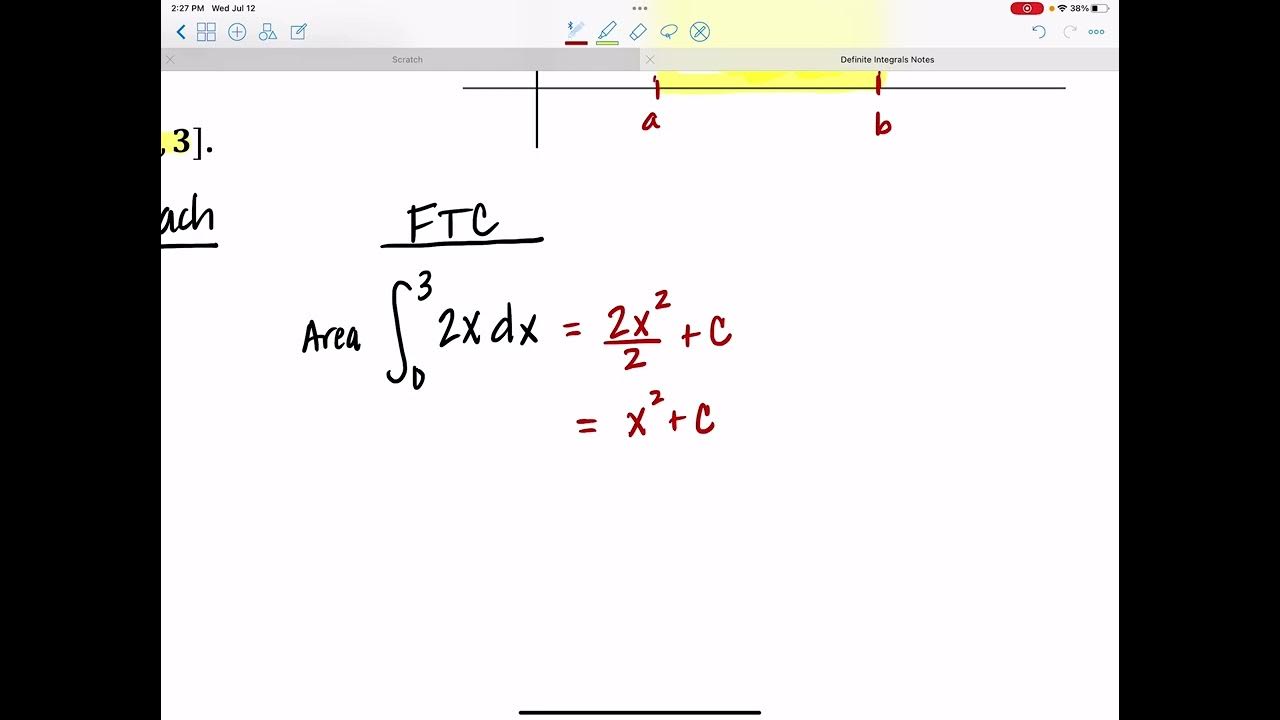
- 📐 The area under a curve represented by the integral from a to b of f(x)dx can be found by evaluating the antiderivative G(x) at point b and subtracting the value of G(x) at point a.
- 🔍 The antiderivative G(x) of a function f(x) is used to find the exact area under the curve, which might seem like a coincidence, but it's not.
- 🤔 To understand why this works, consider finding the area of a two-dimensional shape by multiplying the average height (y-value) by the width (in this case, 3).
- 🧮 The average y-value is found by averaging an infinite number of y-values between 0 and 3, which is essentially finding the average rate of change of the function f(x).
- 📈 The average rate of change is calculated by taking the difference in the function's values at points a and b, divided by the difference in x-values (b - a).
- 📉 To find the average slope (average rate of change) between two points, you take the derivative of the function f'(x) and apply the same process.
- 🎢 The pattern that emerges is that to find the average rate of change of a function, you take the antiderivative evaluated at the end points and subtract.
- 🧠 The process is repeated for the second derivative f''(x) to find the average rate of change of the derivative itself.
- 🔗 The pattern shows that to find the average value of a function over an interval, you take the antiderivative and evaluate it at the interval's endpoints, then subtract.
- ✅ The Fundamental Theorem of Calculus is a direct result of this pattern, allowing us to find the area under a curve by evaluating the antiderivative at the endpoints of the interval.
- 📝 The theorem is restated as the area under the curve of f(x) from a to b is equal to the antiderivative evaluated at b minus the antiderivative at a.
Q & A
What is the fundamental theorem of calculus?
-The fundamental theorem of calculus establishes a relationship between the derivative and the integral. It states that if G(x) is an antiderivative of a function f(x) on the interval [a, b], then the definite integral of f from a to b is equal to G(b) - G(a).
How does the area under a curve relate to the antiderivative of the function that defines the curve?
-The area under the curve of a function f(x) from a to b can be found by evaluating the antiderivative G(x) of f(x) at the point b and subtracting the value of G(x) at the point a. This is because the antiderivative represents the accumulated change in the function, and the difference gives the net area under the curve.
What is the significance of finding the average y-value in the context of the area under a curve?
-The average y-value is significant because it represents a constant rate of change that would yield the same area as the actual curve. Multiplying this average y-value by the width of the interval (b - a) gives an approximation of the area under the curve, which is exact when the curve is a straight line.
How do we find the average rate of change of a function over an interval [a, b]?
-The average rate of change of a function f(x) over an interval [a, b] is found by calculating the difference in the function's values at b and a, divided by the difference in the x-values, which is (f(b) - f(a)) / (b - a).
What is the role of the antiderivative in finding the area under a curve?
-The antiderivative, or integral, of a function reverses the process of differentiation. By evaluating the antiderivative at two points and finding the difference, one can calculate the exact area under the curve between those points.
How can we find the average value of the derivative of a function over an interval [a, b]?
-The average value of the derivative (f'(x)) over an interval [a, b] is found by taking the derivative of the antiderivative (F'(x) = f(x)) and then evaluating it at the endpoints a and b, and dividing the difference by the interval width (b - a).
What is the average rate of change of the derivative of a function?
-The average rate of change of the derivative of a function, which is essentially the second derivative (f''(x)), is found by evaluating the derivative of the antiderivative of the derivative at the endpoints of the interval and dividing the difference by the interval width.
Why is finding the average value of the function important in calculating the area under the curve?
-Finding the average value of the function is important because it provides a simple constant that, when multiplied by the interval width, gives an approximation of the area under the curve. This is particularly useful when the function is not easily integrable in elementary terms.
What is the relationship between the antiderivative and the average value of a function?
-The antiderivative of a function evaluated at two points gives the difference in the accumulated change over the interval, which corresponds to the area under the curve. The average value of the function is the constant rate of change that would yield this area, and it is found by dividing the antiderivative evaluated at the interval endpoints by the interval width.
How does the concept of the average value relate to the idea of integration?
-Integration is the process of finding the accumulated change of a function over an interval, which can be thought of as the area under the curve. The average value of the function over that interval gives a constant rate of change that, when multiplied by the interval width, yields the same area, thus providing a link between the concept of averages and integration.
What is the simplest way to understand the fundamental theorem of calculus?
-The simplest way to understand the fundamental theorem of calculus is to see it as a method for calculating the exact area under a curve by finding the antiderivative of the function that defines the curve and evaluating it at the endpoints of the interval, then subtracting the two values.
Outlines
📚 Understanding the Fundamental Theorem of Calculus
This paragraph introduces the video's purpose: to provide a logical understanding of why the Fundamental Theorem of Calculus works. The presenter explains that the area under a curve is found by evaluating the antiderivative of the function at two points and subtracting them. The audience is encouraged to think about how to determine the area of a two-dimensional shape by multiplying the length by an average height. The key insight is that the antiderivative evaluated at two points gives the exact area under the curve, which might seem coincidental but is actually a result of calculus principles.
📈 Finding the Average Slope and Area Under a Curve
The second paragraph delves into the concept of finding the average slope between two points, which is the average rate of change of the function. The presenter illustrates this with an example, showing how to calculate the average slope by taking the difference in the function's values at two points and dividing by the difference in the x-values. The paragraph then extends this concept to find the average rate of change of the derivative function (f'), and further to find the average value of the function (f) itself. The presenter concludes by connecting these ideas to the Fundamental Theorem of Calculus, which states that the area under the curve of a function can be found by evaluating its antiderivative at two points and subtracting them.
Mindmap
Keywords
💡Fundamental Theorem of Calculus
💡Antiderivative
💡Integral
💡Area Under the Curve
💡Average Value
💡Rate of Change
💡Derivative
💡Slope
💡Total Change
💡Infinite
💡Average Slope
Highlights
The fundamental theorem of calculus allows us to find the area under a curve by evaluating the antiderivative at two points.
If G(x) is the antiderivative of f(x), the area under the curve from a to b is given by G(b) - G(a).
Finding the area under a curve is like finding the area of a two-dimensional shape.
To find the area of a shape, you can multiply the average y value by the width.
The average y value is the y value that divides the area into two equal parts.
To find the average y value, you need to average an infinite number of y values between 0 and 3.
You can find the average slope between two points by taking the total change in y over the total change in x.
The average rate of change is equal to the average of the derivative function.
To find the average rate of change of the derivative, you take the derivative of the derivative and repeat the process.
The pattern is to find the average of a function by taking the antiderivative, evaluating it at two points, and subtracting.
The fundamental theorem of calculus states that the area under the curve of f(x) is equal to the antiderivative evaluated at b minus the antiderivative evaluated at a.
Finding the average value of a function allows you to calculate the area under the curve by multiplying by the width of the interval.
The video provides a simple, intuitive explanation of the fundamental theorem of calculus using geometric and algebraic reasoning.
The explanation helps demystify the "magical coincidence" of the theorem and shows the logical reasoning behind it.
The video uses the concept of averaging an infinite number of values to build up to the main idea.
The presenter encourages viewers to pause and think about the questions posed, promoting active engagement with the material.
The explanation is accessible to those with a basic understanding of calculus, making it a helpful resource for a wide range of learners.
The video promises a follow-up video to further clarify related concepts, indicating a commitment to comprehensive instruction.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: