Area Between Two Curves
TLDRIn this educational video, Professor Monty explains the process of finding the area between two curves, f(x) and g(x). He begins by illustrating the concept using the x-y axis and two intersecting curves, identifying the points of intersection as 'a' and 'b'. The area under the curve f(x), up to the x-axis, is the integral from 'a' to 'b' of f(x)dx. To find the area between the curves, subtract the area under g(x), which is represented by the integral of g(x)dx from the area under f(x). The professor emphasizes that the integral from 'a' to 'b' of the top function minus the bottom function will yield the desired area, and cautions that the order of subtraction matters to avoid a negative result. He then demonstrates the process with a specific problem, showing how to find the points of intersection by setting the functions equal to each other and solving the resulting equation. After determining the top and bottom functions, he integrates from 0 to 3, providing a step-by-step calculation that results in the area between the curves. The video concludes with encouragement to practice the technique and a reminder to like and subscribe for more educational content.
Takeaways
- 📐 To find the area between two curves, integrate the top function minus the bottom function over the interval where they intersect.
- 🔍 Identify the points of intersection (a and b) by setting the two functions equal to each other and solving the resulting equation.
- ➖ Subtract the area under the lower curve (g(x)) from the area under the upper curve (f(x)) to get the area between the curves.
- 🔺 Ensure to choose the correct function as the top and bottom when integrating, as the larger y-value at a given x indicates the top function.
- ⚖️ If you accidentally integrate bottom minus top, you'll get the same numerical result but with a negative sign, which is incorrect for area calculations.
- 🧮 Practice solving systems of equations to find the points of intersection if they are not directly given.
- 📈 The process involves integrating from the lower intersection point (a) to the upper intersection point (b).
- 📉 Be aware that the area under a curve is always a positive value, so a negative result from an integration indicates an error in the setup.
- 🎯 When plugging in a value to determine which function is on top, choose a value that lies between the intersection points.
- 🧮 After finding the top and bottom functions, integrate the expression representing the difference between them over the interval [a, b].
- 📘 The integral of the difference of the functions will give the area between the curves, which is the final answer to the problem.
- 💡 Keep practicing to become more comfortable with the process, as it can be challenging when dealing with fractions or complex functions.
Q & A
What is the method to find the area between two curves?
-The area between two curves is found by integrating the top function minus the bottom function from the points where they intersect, denoted as 'a' and 'b'.
Why is it necessary to find the points of intersection (a and b) for the two curves?
-The points of intersection (a and b) are the bounds of integration. They define the limits between which the area under the curves is calculated.
How does one determine which function is the top function and which is the bottom function?
-To determine the top and bottom functions, choose a test point within the interval of integration and plug it into both functions. The function with the larger value at that point is the top function.
What happens if you accidentally integrate the bottom function minus the top function instead of the top minus the bottom?
-If you integrate the bottom function minus the top function, you will get the same numerical result but with the wrong sign. Since area cannot be negative, this would indicate an error in the calculation.
In the given problem, what are the two functions whose area between them needs to be found?
-The two functions are f(x) = x^2 - 2x and g(x) = x.
How does one find the points of intersection for the functions f(x) and g(x)?
-To find the points of intersection, set the two functions equal to each other and solve the resulting equation for x.
What is the integral expression used to find the area between the two curves in the given problem?
-The integral expression is ∫ from a to b of (x - (x^2 - 2x)) dx, where 'a' and 'b' are the points of intersection.
What is the result of the integral in the given problem?
-The result of the integral is 9/2 or 4.5, which represents the area between the two curves from x = 0 to x = 3.
Why is it important to add 1 to the exponent and multiply by the reciprocal when integrating a polynomial?
-This is a standard step in integrating polynomials. It simplifies the integration process by reducing the power of x in the integral, making it easier to solve.
What is the significance of evaluating the integral at the bounds (from 0 to 3 in the given problem)?
-Evaluating the integral at the bounds gives the definite value of the area between the curves over the specified interval, which is necessary for finding the exact area.
How does Professor Monty encourage viewers to improve their understanding of finding areas between curves?
-null
Outlines
📐 Finding Area Between Two Curves
Professor Monty introduces a method for calculating the area between two curves, labeled 'f' and 'g'. He explains that to find the area, one must first identify the points of intersection 'a' and 'b'. The area under the curve 'f' is calculated by integrating from 'a' to 'b', but since this includes the area under the x-axis, the area under the lower curve 'g' is subtracted. Monty emphasizes that the result is always the integral of the top function minus the bottom function. He then demonstrates the process with a problem, finding the points of intersection by setting the functions equal to each other and solving the resulting equation. Monty integrates from 0 to 3, using the top function minus the bottom function, and concludes with the integral calculation, which yields the area between the curves.
🧮 Completing the Integral Calculation
Continuing from the previous explanation, Monty completes the integral calculation for the area between the two curves. He simplifies the integral to -x^2 + 3x and applies the standard integration technique, which results in (-1/3)x^3 + (3/2)x^2. Evaluating this expression from 0 to 3, he finds the area to be (-27 + 27) - (0 + 0), which simplifies to 0. Monty then corrects the calculation, noting that the actual result should be (-1/3 * 27 + 9/2 * 3) - (-1/3 * 0 + 9/2 * 0), leading to a final area of 9/2 or 4.5 square units. He reminds viewers that the area cannot be negative and encourages practice, suggesting that the key is to integrate the top function minus the bottom function and to solve the system of equations to find the intersection points if they are not given.
Mindmap
Keywords
💡Area between curves
💡Integration
💡Functions
💡Intersection points
💡Top function and bottom function
💡System of equations
💡Substitution method
💡Factoring
💡Exponent
💡Reciprocal
💡Power rule
Highlights
The area between two curves can be found by integrating the top function minus the bottom function from the points where they intersect.
To find the points of intersection, set the two functions equal to each other and solve the resulting equation.
Factor out the common variable (e.g. x) to solve for the points of intersection.
Choose the larger function value at a test point between the intersection points as the top function for the integral.
The integral of the top function minus the bottom function gives the area between the curves.
If you accidentally do bottom minus top, you get the same numerical result but with a negative sign, which doesn't make sense for area.
Always integrate from the lower x-intercept (point A) to the higher x-intercept (point B).
When finding the top and bottom functions, plug in a test x-value between the intersection points to determine which function is higher.
The area under the curve is always positive, so ensure the integral result makes sense as a physical area.
Use the power rule to integrate the polynomial functions representing the top and bottom curves.
Add 1 to the exponent and multiply by the reciprocal of the new exponent when integrating a polynomial term.
Evaluate the definite integral by plugging in the upper and lower limits of integration.
Simplify the result to get the final area between the curves, which should be expressed in a positive, simplified form.
Practice finding areas between curves by working through different problems to build proficiency.
Don't get caught up in the numbers - focus on understanding the process and applying the method consistently.
Sometimes fractions can make the problem more challenging, but the same principles apply.
Remember to find the points of intersection first, then determine the top and bottom functions before integrating.
The area between curves is a fundamental concept in calculus with practical applications in various fields.
Transcripts
Browse More Related Video

Area between two curves (using a calculator) - AP Calculus
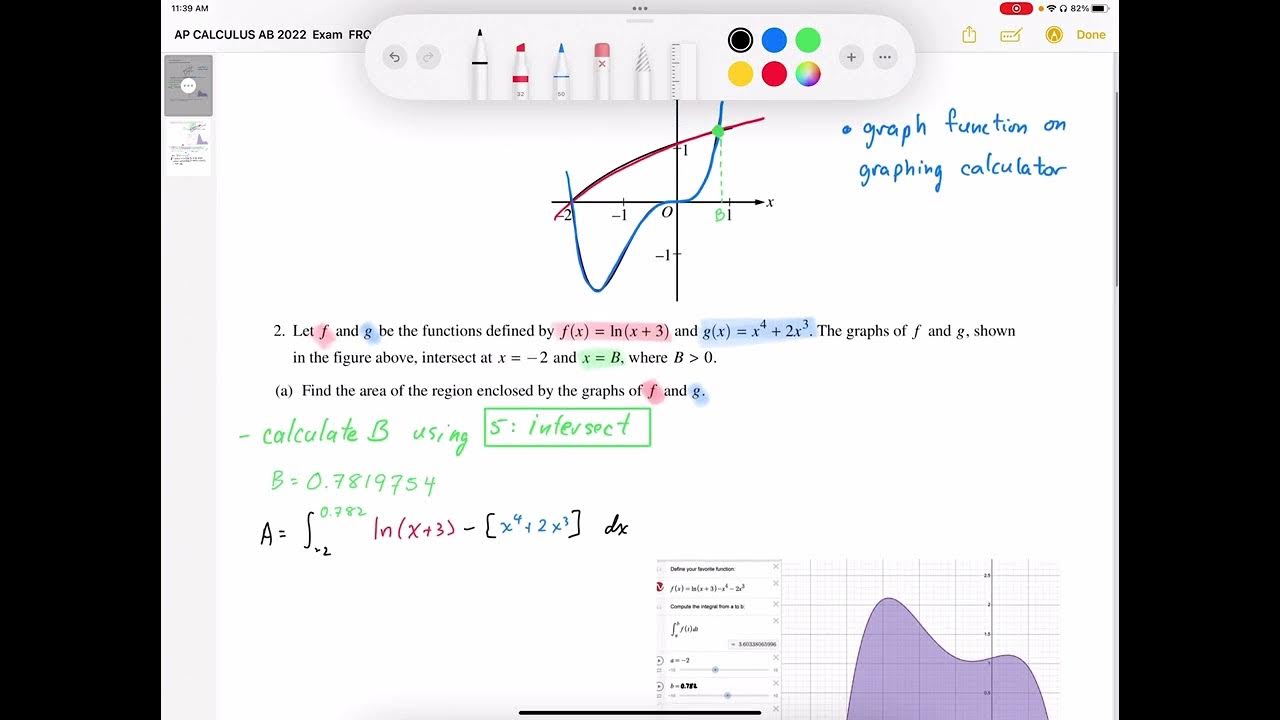
AP CALCULUS AB 2022 Exam Full Solution FRQ#2a

An Intuitive Understanding of the Fundamental Theorem of Calculus

Area Between Curves: Integrating with Respect to y (Example 2)
2015 AP Calculus AB Free Response #2

Fundamental Theorem of Calculus Explained | Outlier.org
5.0 / 5 (0 votes)
Thanks for rating: