Calculus 1 Lecture 4.5: The Fundamental Theorem of Calculus

Professor Leonard

22 Jan 2014166:09

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is an engaging and detailed explanation of calculus concepts, focusing on the fundamental theorem of calculus and the application of definite integrals. The speaker delves into the geometric interpretation of integrals as areas under curves and introduces the concept of antiderivatives. They also discuss the importance of understanding the relationship between derivatives and integrals as inverse operations. The script explores the use of substitution in evaluating integrals, emphasizing the need for careful selection of substitution variables and the manipulation of integral expressions. The speaker further illustrates how to handle piecewise functions and the application of even and odd function properties in integral calculus. The narrative is enriched with practical examples and a step-by-step approach to solving integrals, making the complex topic of calculus more accessible to learners.

Takeaways

📚 The Fundamental Theorem of Calculus Part 2 states that the definite integral of a function can be found by evaluating the antiderivative of the function at the bounds of integration and subtracting the results.
🔍 The process of calculating definite integrals involves finding the antiderivative (also known as the integral) of the function and then applying the bounds of integration.
📈 The concept of 'net signed area' refers to the total area under the curve of a function from one point to another, taking into account the sign (positive or negative) of the function's value at different points.
🤔 The 'plus C' in indefinite integrals represents a constant that is eliminated when calculating definite integrals because it cancels out when you subtract the integral evaluated at the lower bound from that evaluated at the upper bound.
📉 When dealing with functions that are undefined or unbounded within the interval of integration, the integral may not represent a meaningful area and could be considered undefined or infinite.
🤓 The choice of substitution for integration should be based on the innermost function or the function that can be easily eliminated by differentiation, often involving a chain rule.
🧩 The process of substitution in integration involves changing the variable of integration to simplify the integral, and it's crucial to also change the differential (e.g., from dx to du).
✅ To evaluate a definite integral, one must plug in the upper and lower bounds of integration into the antiderivative and subtract the results.
🔢 The Fundamental Theorem of Calculus Part 1 establishes the relationship between differentiation and integration, stating that the derivative of an integral from a to x of a continuous function is equal to the function itself.
➗ When a function is split into piecewise parts, the integral of the function can be broken down into the sum of integrals of each part over their respective intervals.
⛔ It's important to recognize when a function is even or odd, as this can simplify the integration process. An even function is symmetric about the y-axis, and an odd function is symmetric about the origin.

Q & A

What is the fundamental theorem of calculus?
-The fundamental theorem of calculus is divided into two parts. Part one states that differentiation and integration are inverse operations, meaning one undoes the other. Part two is about calculating definite integrals by finding antiderivatives and evaluating them at the limits of integration, which represents the area under the curve.
Why is the constant of integration (C) often dropped when dealing with definite integrals?
-The constant of integration (C) is dropped in definite integrals because when you evaluate the antiderivative at the upper and lower limits of integration and subtract, the constants cancel each other out. This leaves you with the specific value representing the area under the curve between the two limits, which is what a definite integral represents.
How does the concept of a dummy variable simplify the process of integration?
-A dummy variable, often represented as 'u' or 't', is used to simplify the integration process by allowing the integrator to work with a new variable that is not 'x'. This is particularly useful when the bounds of integration are in terms of 'x'. After integrating, the dummy variable is replaced back with 'x' to reflect the original variable of the function.
What is the purpose of a sign analysis test in the context of definite integrals?
-A sign analysis test is used to determine where a function is positive or negative within a given interval. This is crucial for definite integrals because it helps to identify where the function lies above or below the x-axis, which in turn affects the calculation of the net signed area (the area that considers the sign of the function).
How does the concept of even and odd functions relate to the computation of definite integrals?
-Even functions are symmetric about the y-axis, and their integral from negative to positive values of the same magnitude is twice the integral from zero to that positive value. Odd functions, which are symmetric about the origin, have the property that their integral from negative to positive values of the same magnitude equals zero, because the areas above and below the x-axis cancel each other out.
What is the process of substitution in integration, and when is it typically used?
-Substitution is a method used in integration when the integral does not fit directly into standard forms or when the integral involves a complex expression that can be simplified. The process involves replacing a part of the integrand with a new variable, which often leads to a simpler integral. The bounds of integration may also change accordingly.
What is the significance of the absolute value in the context of total area calculations?
-The absolute value is used to calculate the total area between two curves without considering the sign of the function. It converts any negative areas to positive, allowing for the addition of areas that lie above and below the x-axis to find the total area enclosed by the curves.
How does the Fundamental Theorem of Calculus Part 1 relate to finding derivatives of integrals?
-Fundamental Theorem of Calculus Part 1 establishes that the derivative of an integral from a to x of a continuous function f(t) dt is simply the function f(x). This means that the process of integration can be reversed by differentiation, which is particularly useful for evaluating definite integrals and finding area functions.
What is the role of the chain rule in the context of substitution in integration?
-The chain rule is essential in the context of substitution in integration. It allows you to find the derivative of a composite function, which is necessary when you substitute a new variable into the integral. Specifically, it helps in finding the differential 'du' or 'dx' in terms of the new variable 'u', which is then used to rewrite the integral in a more manageable form.
What are the two methods for handling the bounds of integration when using substitution, and what are their differences?
-The two methods are: 1) Not changing the bounds and substituting back in for the substitution variable before evaluation, which is a straightforward approach that keeps the original bounds and ensures the function is in terms of 'x' before integrating. 2) Changing the bounds during the first substitution, which involves converting the bounds of integration into terms of the new variable and does not require substituting back in for 'x' before evaluating, as the evaluation is done directly in terms of the new variable.
Why is it important to determine whether a function is even or odd before applying certain integral properties?
-Determining if a function is even or odd is important because it allows you to apply specific properties that simplify the integration process. For even functions, the integral from negative to positive values of the same magnitude can be simplified by calculating the integral from zero to the positive value and multiplying by two. For odd functions, the integral from negative to positive values of the same magnitude is zero, which can bypass the need for integration entirely.

Outlines

00:00

😀 Introduction to the Fundamental Theorem of Calculus

The speaker introduces the topic of the fundamental theorem of calculus, emphasizing the excitement around it. They discuss the concept of 'good stuff' in calculus, such as derivatives, integrals, and the fundamental theorem itself. The audience is encouraged to visualize calculus problems, like areas under curves, and the connection between integrals and antiderivatives.

05:01

📚 Understanding Definite Integrals as Areas

The paragraph delves into the concept of definite integrals, explaining how they represent the area under a curve from one point to another. The process of calculating this area without using Riemann sums is discussed, along with the idea of subtracting areas to find the desired integral. The importance of understanding the concept behind the calculations is highlighted.

10:01

🔢 The Role of Constants in Indefinite Integrals

The discussion shifts to the role of the constant 'C' in indefinite integrals. It is clarified that while the constant appears in indefinite integrals, it cancels out in definite integrals. The reason for this is that the definite integral is concerned with a specific area, and the constant represents a family of curves that are vertically shifted versions of each other.

15:02

🧮 Practical Calculations of Definite Integrals

The speaker provides examples of calculating definite integrals, emphasizing the practicality and simplicity of the process. They illustrate how to perform the calculations by plugging in the limits of integration into the antiderivative of the function. The examples include integrals of polynomials and trigonometric functions, and the importance of understanding the function's behavior is stressed.

20:03

📉 Contemplating the Area Under Trigonometric Curves

The focus is on the area under the curve of trigonometric functions, specifically cosine. The integral of cosine from zero to π/2 is calculated, resulting in an area of one. The implications of this result are explored, including the observation that the area of a circle's quarter is equal to one in this context.

25:04

🤔 Dealing with Discontinuous Functions in Integration

The challenges of integrating discontinuous functions are addressed. The speaker explains that if a function has an asymptote or is unbounded within the interval of integration, the integral may be undefined or require a different approach. The importance of understanding the function's behavior and the domain of integration is emphasized.

30:07

📌 Correctly Ordering Bounds of Integration

The importance of having bounds of integration in the correct order is discussed. It is shown that if the bounds are reversed, the sign of the integral changes, which can lead to confusion about the area represented by the integral. The concept of net signed area is introduced, which accounts for areas above and below the x-axis.

35:08

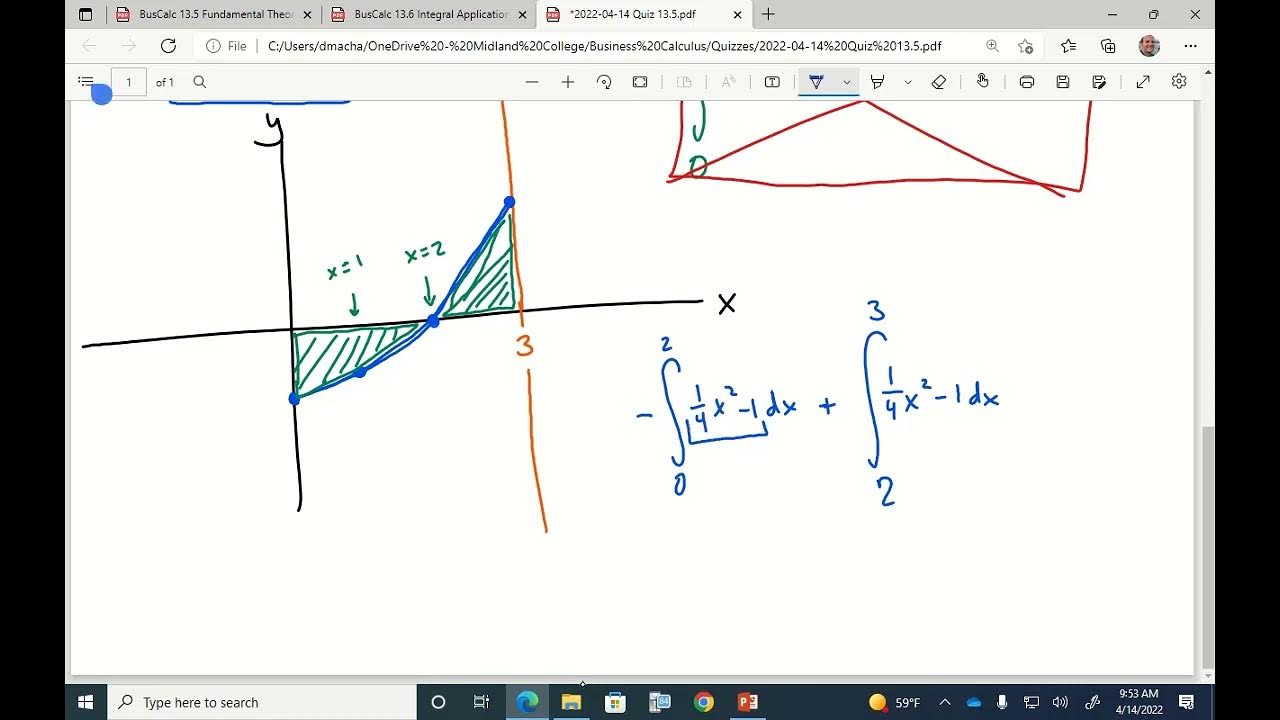
🔠 Working with Piecewise Functions in Integration

The paragraph discusses the integration of piecewise functions, where the function's rule changes at certain points. The speaker explains that integrals can still be calculated by breaking them up into separate integrals for each piece, as long as the function is continuous over the entire interval.

40:09

🔢 Evaluating Definite Integrals with Substitution

The process of evaluating definite integrals using substitution is explained. The speaker presents two methods: one where the bounds are not changed during substitution, and another where the bounds are changed to match the substituted variable. The importance of correctly applying the substitution and evaluating the integral is emphasized.

45:13

📐 Splitting Up Definite Integrals for Evaluation

The speaker illustrates how to split up a definite integral into two or more parts, especially when the function's sign changes within the interval of integration. This allows for the calculation of the net signed area, which accounts for both positive and negative areas under the curve.

50:14

🧐 Identifying Even and Odd Functions for Integration

The properties of even and odd functions in the context of integration are discussed. For even functions, the integral from negative to positive 'a' can be simplified by calculating the integral from zero to 'a' and then doubling it. For odd functions, the integral from negative to positive 'a' is zero because the areas on either side of the y-axis cancel each other out.

55:15

🎯 Applying Properties of Even and Odd Functions

The practical application of identifying even and odd functions to simplify integration is shown. The speaker demonstrates how proving a function's evenness or oddness can lead to significant simplifications in calculating integrals, especially when direct integration or substitution is not straightforward.

Mindmap

Keywords

💡Antiderivatives

Antiderivatives, also known as indefinite integrals, are functions that represent the reverse process of differentiation. In the video, it is mentioned that antiderivatives are used to calculate the area under a curve, which is a key concept in the Fundamental Theorem of Calculus. The script illustrates this by saying 'an integral represents an area' and discussing how to find antiderivatives of functions like x^2 and cosine(x).

💡Definite Integrals

A definite integral is a concept in calculus that represents the exact area under a curve between two points on the x-axis. The video emphasizes the calculation of definite integrals by finding the difference between the antiderivative evaluated at the upper and lower limits of integration. This is demonstrated in the script with examples such as the integral from 1 to 5 of x dx and the integral from 0 to π/2 of cos(x) dx.

💡Fundamental Theorem of Calculus

The Fundamental Theorem of Calculus is a central theorem that connects differentiation and integration, showing they are inverse operations. The video discusses both parts of the theorem: part one states that the integral of a derivative is the original function, and part two states that the derivative of an integral from a to x is the function itself. This is a pivotal concept in the script, as it underpins the method for evaluating definite integrals.

💡Substitution

Substitution is a technique used in calculus to simplify integrals that do not fit standard forms. The video explains how to use substitution, particularly when the integral involves functions of the form (sin(x))^n or (cos(x))^n. The script demonstrates the substitution method by showing how to change the bounds of integration and how to apply the substitution to the integral itself, which simplifies the process of finding the antiderivative.

💡Net Signed Area

Net signed area refers to the calculation of the area under a curve that takes into account the sign (positive or negative) of the function's values. The video explains that a definite integral automatically computes the net signed area, which is the sum of the areas above the x-axis minus the areas below the x-axis. This concept is illustrated in the script with examples where the function crosses the x-axis, resulting in both positive and negative contributions to the area.

💡Piecewise Functions

Piecewise functions are defined by different expressions over different intervals of the domain. The video discusses how to handle integrals involving piecewise functions by breaking the integral into separate parts corresponding to each interval. The script shows an example where a function is defined as x^3 for x < 2 and as 5x - 1 for x ≥ 2, and how to calculate the integral over the range from 0 to 6 by splitting it into two parts.

💡Riemann Sums

Riemann sums are a method for approximating the area under a curve by breaking it into rectangles. The video contrasts the use of Riemann sums with the more straightforward method of using antiderivatives to find the exact area. The script mentions Riemann sums as an alternative approach but focuses on the antiderivative method as being simpler and more direct.

💡Total Area

Total area is the sum of all areas under a curve, regardless of whether they are above or below the x-axis. The video explains how to calculate the total area by using the absolute value of the function within the integral. This is demonstrated in the script by showing how the absolute value can change negative areas to positive, thus allowing the calculation of the total area as a sum of absolute values of areas.

💡Trigonometric Integrals

Trigonometric integrals involve functions based on trigonometric functions, such as sine or cosine. The video provides specific examples of how to integrate functions like cos(x) and sec(x)^2. The script demonstrates the integration of cos(x) by showing that the integral of cos(x) is sin(x), which is a standard result in calculus used to find areas under trigonometric curves.

💡U-Substitution

U-substitution, also known as reverse chain rule, is a method used to transform an integral that is difficult to solve directly into a simpler form. The video explains the process of choosing a substitution variable (u), changing the differential (du), and transforming the integral accordingly. The script illustrates u-substitution with examples, showing how to solve integrals that involve powers of trigonometric functions or expressions that can be related to a new variable u.

Highlights

Introduction to the Fundamental Theorem of Calculus, which connects differentiation and integration.

Explanation of how the integral of a function can represent an area under a curve.

Discussion on the concept of antiderivatives and their role in evaluating definite integrals.

Use of the '+' C in indefinite integrals and why it disappears in definite integrals.

Visual representation of integrals as areas on a graph, aiding in understanding the geometric interpretation.

Technique for calculating definite integrals without using Riemann sums or summation notation.

The process of subtracting the integral evaluated at a lower bound from the integral evaluated at an upper bound.

Integration of functions like x and cosine(x), including the results and their interpretations.

Explanation of the Net Signed Area and how it differs from Total Area in the context of definite integrals.

Introduction to the concept of a piecewise function and how to handle integrals of such functions.

Discussion on the properties of even and odd functions and their impact on integrals.

Practical application of substitution in integrals to simplify complex expressions.

Method of changing the bounds of integration when performing a substitution to simplify the evaluation.

Use of the absolute value function to find the total area under a curve without considering the sign of the function's values.

The importance of understanding the domain of a function when calculating integrals and the potential issues with undefined points.

Strategy for integrating functions involving trigonometric functions and the application of substitution method.

Demonstration of how to set up and evaluate a definite integral using properties of even and odd functions to simplify the process.

Final example illustrating the evaluation of a complex integral using substitution and properties of trigonometric functions.

Transcripts

Browse More Related Video

Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions

BusCalc 13.6 Integral Applications

Definite Integrals!

Math 1325 Lecture 13 2

AP Calculus AB: Lesson 6.3 Fundamental Theorem of Calculus Part 1

Lec 20 | MIT 18.01 Single Variable Calculus, Fall 2007

Related Tags

Calculus Integrals Derivatives Substitution Even Functions Odd Functions Mathematical Properties Theorem Application Trigonometric Functions Area Calculation