Calculus AB/BC – 6.4 The Fundamental Theorem of Calculus and Accumulation Functions

The Algebros
10 Dec 202011:54
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging calculus lesson, Mr. Bean introduces the concept of accumulation functions and the fundamental theorem of calculus. He explains how to calculate the area under a curve using definite integrals and how to derive an integral when the upper limit is a variable. Through step-by-step examples, he demonstrates the process of taking derivatives of integrals with variable upper bounds, emphasizing the inverse relationship between derivatives and integrals. The lesson aims to simplify complex concepts, making them accessible for learners new to calculus.

Takeaways
  • πŸ“š The definite integral symbol represents the area under the curve on a specific interval from a to b.
  • πŸ” If the upper limit is unknown (x), the integral from a to x represents an accumulation function, f(x).
  • πŸ“ˆ The accumulation function is visualized on a graph by plotting points and connecting them to show the area under the curve.
  • 🌟 The fundamental theorem of calculus states that the derivative of an integral is the original function (integrand).
  • βš–οΈ Derivatives and integrals are inverse operations, similar to how multiplication and division are inverses.
  • πŸ“ When differentiating an integral with a variable upper bound, simply substitute the variable into the integrand.
  • πŸ”’ For more complex integrals with expressions, apply the chain rule when differentiating with respect to the variable.
  • πŸ”„ When the upper and lower limits are variables, apply the chain rule and subtract the lower limit's derivative from the upper limit's.
  • πŸŽ“ The process of accumulation function differentiation involves plugging in values and applying algebraic simplification.
  • πŸ› οΈ Practice is key to understanding the concepts of accumulation functions and the fundamental theorem of calculus.
  • πŸ“ˆ The derivative of an integral can result in a polynomial function, showcasing the relationship between the integral and the original function.
Q & A

  • What does the definite integral represent?

    -The definite integral represents the area under the curve of a function on a specific interval from a to b.

  • What happens when the upper limit of an integral is an unknown variable?

    -When the upper limit of an integral is an unknown variable, it creates an indefinite integral, which represents an accumulation function that varies with the unknown variable.

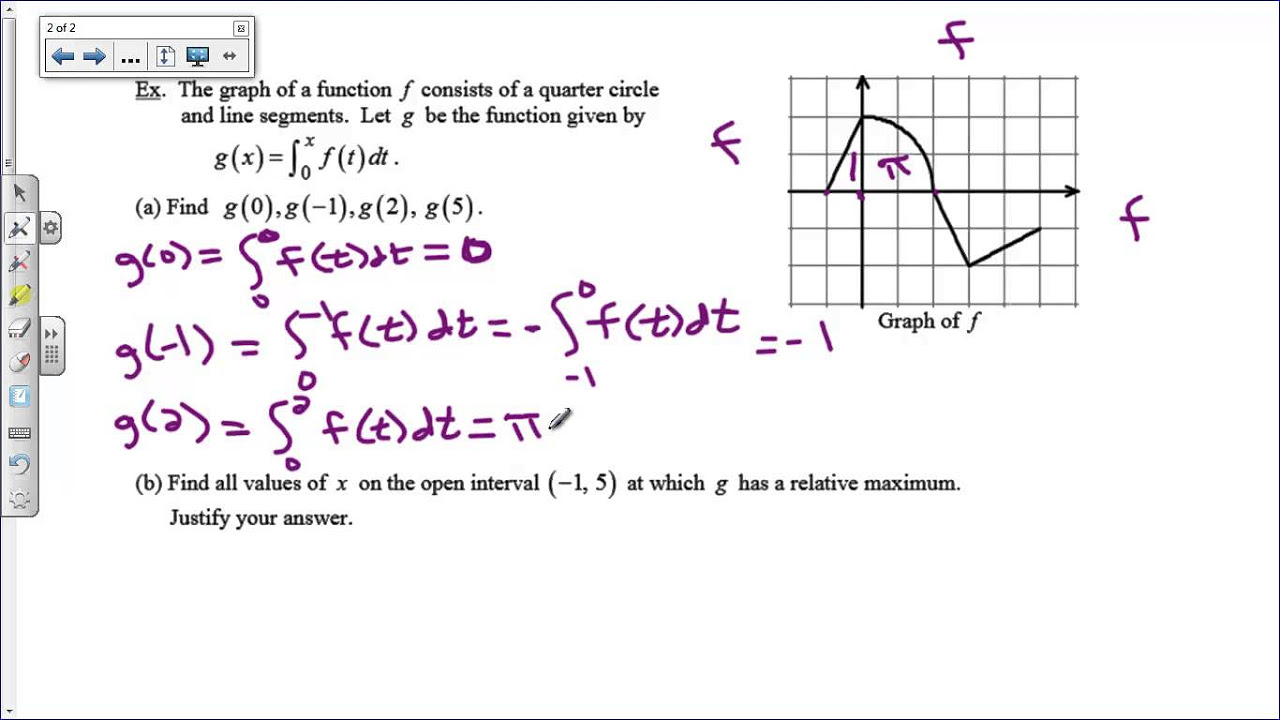
  • How does the accumulation function change as x varies from 0 to different values?

    -As x varies, the accumulation function increases or decreases, depending on whether the graph is above or below the x-axis, representing the area under the curve from 0 to the current value of x.

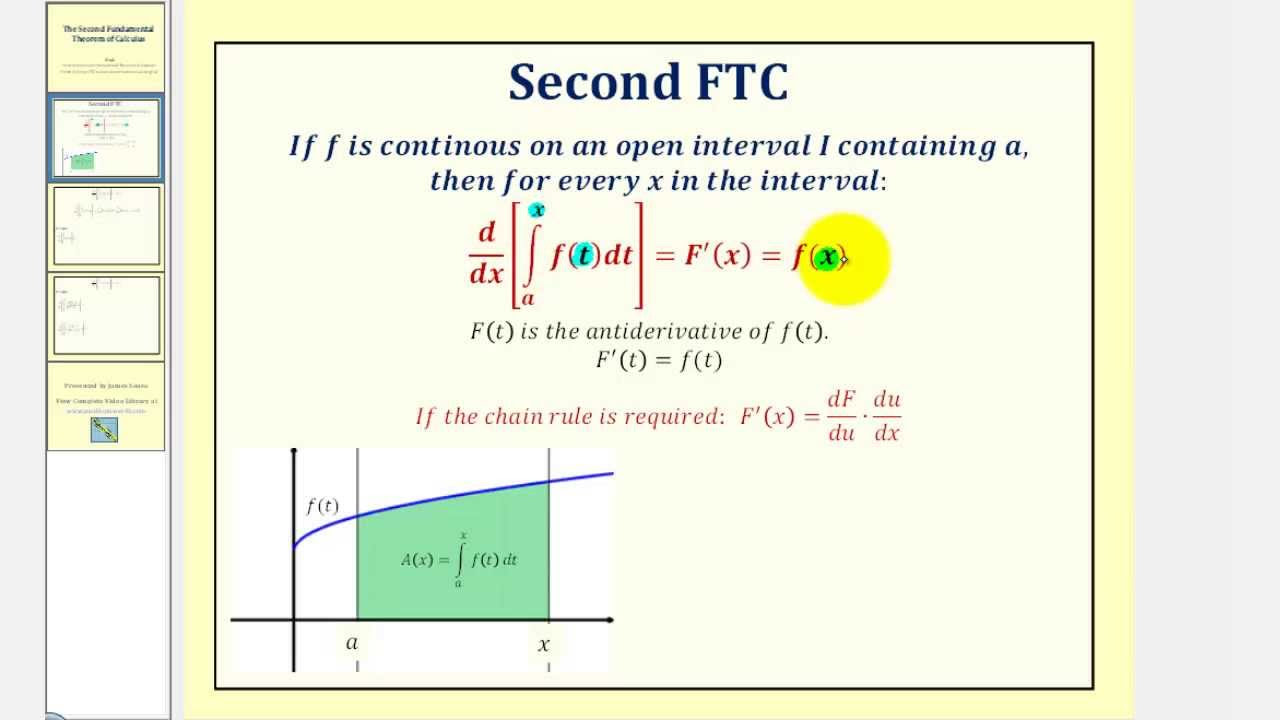
  • What is the fundamental theorem of calculus, and how does it relate to integrals and derivatives?

    -The fundamental theorem of calculus states that derivatives and integrals are inverse operations. The derivative of an integral returns the original function (the integrand), and the integral of a derivative returns the original function (the antiderivative).

  • How does the chain rule apply to the derivative of an integral with a variable upper limit?

    -When the upper limit is a variable expression, the chain rule is applied by substituting the variable into the function and multiplying by the derivative of the plugged-in variable.

  • What is the result of the derivative of the integral from 0 to x of 3x^2 + 4x?

    -The derivative of the integral from 0 to x of 3x^2 + 4x is simply 3x^2 + 4x, with the constant 'a' from the original integral becoming 'x' after substitution.

  • How do you handle a derivative with both upper and lower limits as variables?

    -You substitute the upper limit into the function, apply the chain rule by multiplying by the derivative of the upper limit, and then subtract the result of substituting the lower limit into the function, again applying the chain rule by multiplying by the derivative of the lower limit.

  • What is the accumulation function in the context of the integral from 0 to x of f(t) dt?

    -The accumulation function, denoted as capital F, is the function that represents the area under the curve of f(t) from 0 to x, accumulating as x increases.

  • How does the derivative of an integral with a constant on the bottom and variables on top work?

    -If the lower limit is a constant and the upper limit is a variable expression, you simply substitute the variable into the function and multiply by the derivative of the plugged-in variable, ignoring the constant lower limit.

  • What is the process for finding the derivative of an integral with an upper limit of g(x) and a lower limit of h(x)?

    -The derivative is found by substituting the upper limit g(x) into the function, applying the chain rule, and subtracting the result of substituting the lower limit h(x) into the function after applying the chain rule with the derivative of the lower limit.

Outlines
00:00
πŸ“š Introduction to Accumulation Functions and the Fundamental Theorem of Calculus

This paragraph introduces the concept of accumulation functions and the fundamental theorem of calculus. Mr. Bean explains that the integral symbol represents the area under a curve on a specific interval, and how to calculate it when the upper limit is unknown. He then discusses the accumulation function, which is used to find the area under the curve as the upper limit variable increases. The fundamental theorem of calculus is briefly mentioned, setting the stage for further discussion in later lessons.

05:02
πŸ”„ Derivatives and Integrals as Inverse Operations

In this section, the relationship between derivatives and integrals as inverse operations is explored. It is explained that taking the derivative of an integral results in the integrand, and vice versa. The concept is illustrated with examples, showing how to apply the chain rule when the upper bound is a function. The explanation emphasizes the cancellation effect between derivatives and integrals, akin to multiplication and division.

10:04
πŸ“ˆ Calculating Derivatives of Accumulation Functions with Variable Limits

This paragraph delves into the process of calculating the derivative of an accumulation function when both the upper and lower limits are variables. A detailed explanation is provided on how to handle such cases, including the application of the chain rule. Several examples are worked out to demonstrate the process, showing how to simplify the expressions and combine like terms to arrive at the final derivative form.

Mindmap
Keywords
πŸ’‘Definite Integral
A definite integral represents the area under the curve of a function over a specific interval, from a lower limit 'a' to an upper limit 'b'. In the context of the video, it is used to introduce the concept of integration and how it can be visualized as the accumulation of area under a curve.
πŸ’‘Integral
An integral is a mathematical concept used to calculate the area under a curve, the volume of solid figures, and more. In the video, the integral symbol is introduced as representing the sum of all numbers under the curve, which is akin to finding the area in a geometric sense.
πŸ’‘Accumulation Function
An accumulation function is a representation of how the area under the curve changes as the upper limit of integration varies. It is used to illustrate the process of accumulation as the upper limit moves from 'a' to 'x', showing how the area under the curve increases or decreases.
πŸ’‘Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus is a key result that connects the concepts of differentiation and integration. It states that the process of differentiation and integration are essentially inverse operations. In the video, this theorem is introduced as a way to understand how the derivative of an integral results in the original function.
πŸ’‘Derivative
A derivative is a concept in calculus that represents the rate of change or the slope of a function at a particular point. In the video, derivatives are used to find the rate of change of an accumulation function and to understand how the integral and the derivative of a function are inverse operations.
πŸ’‘Anti-Derivative
An anti-derivative, also known as an indefinite integral, is a function whose derivative is the given function. It is the reverse process of differentiation. In the video, the anti-derivative is introduced as the integral of a function, which when differentiated, gives back the original function.
πŸ’‘Chain Rule
The chain rule is a technique in calculus used to find the derivative of a composite function. It involves differentiating the outer function and then multiplying by the derivative of the inner function. In the video, the chain rule is applied when taking the derivative of an accumulation function with a variable upper limit.
πŸ’‘Power Rule
The power rule is a basic differentiation rule in calculus that states if you have a function of the form f(x) = x^n, where n is a constant, then the derivative f'(x) = n * x^(n-1). The video uses the power rule to find the derivative of functions involving variables raised to powers.
πŸ’‘Graphing
Graphing is the process of visually representing the behavior of a function on a coordinate plane. In the video, graphing is used to illustrate the accumulation of area under the curve as the upper limit of integration changes, and to visualize the accumulation function.
πŸ’‘Variable Upper Limit
A variable upper limit in integration means that the upper bound of the interval over which the integral is taken is not a fixed number but a variable that can change. In the video, this concept is used to introduce the idea of an accumulation function and to show how the area under the curve changes as the variable upper limit moves.
Highlights

Introduction to the concept of integrals as areas under curves on specific intervals.

Explanation of the integral symbol and its representation of the sum of all numbers under the curve.

Discussion on what happens when the upper limit of integration is an unknown variable.

Illustration of the accumulation of area under the curve as the variable x increases.

Introduction to the accumulation function and its role in calculus.

Explanation of the fundamental theorem of calculus, specifically its second part.

Derivation of the relationship between derivatives and integrals as inverse operations.

Practical example of taking the derivative of an integral with a variable upper bound.

Use of the chain rule when the upper bound is a function of x.

Demonstration of how to handle integrals with both upper and lower bounds as variables.

Step-by-step walkthrough of a complex derivative calculation involving variables in both bounds.

Emphasis on the importance of understanding accumulation functions and the fundamental theorem of calculus for mastery in calculus.

Reassurance that the concepts, although initially confusing, will become clearer with further study.

The lesson's focus on practicing the derivative of integrals with variable upper bounds.

Explanation of how to apply the chain rule when the upper bound is a function involving x.

Detailed example of calculating the derivative of an integral with both bounds being functions of x.

Final practice problem involving the derivative of an accumulation function with variable bounds.

Summary of the key concepts covered in the lesson andι’„ε‘Š for future lessons on the fundamental theorem of calculus.

Transcripts

Browse More Related Video

Calculus AB/BC – 6.7 The Fundamental Theorem of Calculus and Definite Integrals

Calculus 1 Lecture 4.5: The Fundamental Theorem of Calculus

FTC #2

02 - Fundamental Theorem of Calculus, Part 1 - Learn Antiderivatives & Derivatives

AP Calculus AB: Lesson 6.6 Fundamental Theorem of Calculus, Part 2

The Second Fundamental Theorem of Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus LessonsIntegral ConceptsAccumulation FunctionsFundamental TheoremEducational HumorBean's TutorialMathematics EducationLighthearted LearningIntegral DerivativesMath Comedy