How to Use Product to Sum and Sum to Product Formulas in Trig (Precalculus - Trigonometry 29)
TLDRThis video script offers an insightful exploration into trigonometric identities, specifically focusing on sum-to-product and product-to-sum formulas. The presenter begins by demonstrating the mathematical process of transforming products of cosine and sine functions into sums and vice versa, using the sum and difference formulas for these trigonometric functions. The script then delves into practical examples, illustrating how these formulas can simplify complex expressions involving angles not typically found on the unit circle. The presenter emphasizes the utility of these transformations in solving equations more efficiently, particularly by leveraging the zero product property. The script concludes with an application of these concepts to solve trigonometric equations, highlighting the importance of maintaining the correct order of angles and the use of appropriate identities for simplification. The video is an excellent resource for those looking to deepen their understanding of trigonometric identities and their applications in mathematics.
Takeaways
- 📚 The video introduces sum-to-product and product-to-sum trigonometric identities, which are essential for simplifying expressions and solving equations involving sine and cosine functions.
- 🔍 The process of proving these identities involves adding and subtracting known trigonometric formulas to cancel out terms and isolate the desired product or sum.
- 🧮 By manipulating trigonometric expressions, one can convert products of sines or cosines into sums, and vice versa, which is particularly useful for working with angles not on the unit circle.
- 📈 The video demonstrates how to apply these identities with several examples, showing how to find exact values for products of trigonometric functions for angles not typically found on the unit circle.
- ⚖️ The importance of maintaining the correct order when adding or subtracting angles is emphasized, as is the need to use appropriate trigonometric identities when changing the signs of angles.
- 🤔 The video explains the utility of converting sums to products to use the zero product property, which simplifies the process of solving equations.
- 🔢 Specific formulas are provided for adding or subtracting sine functions with different angles, as well as for cosine functions, allowing for the simplification of complex expressions.
- 📉 The concept of even and odd functions in trigonometry is discussed, noting how this affects the simplification process, particularly with cosine as an even function and sine as an odd function.
- 🔁 The video uses the substitution method to solve equations involving the sine function, highlighting how the period of the function can be adjusted to find solutions within a given range.
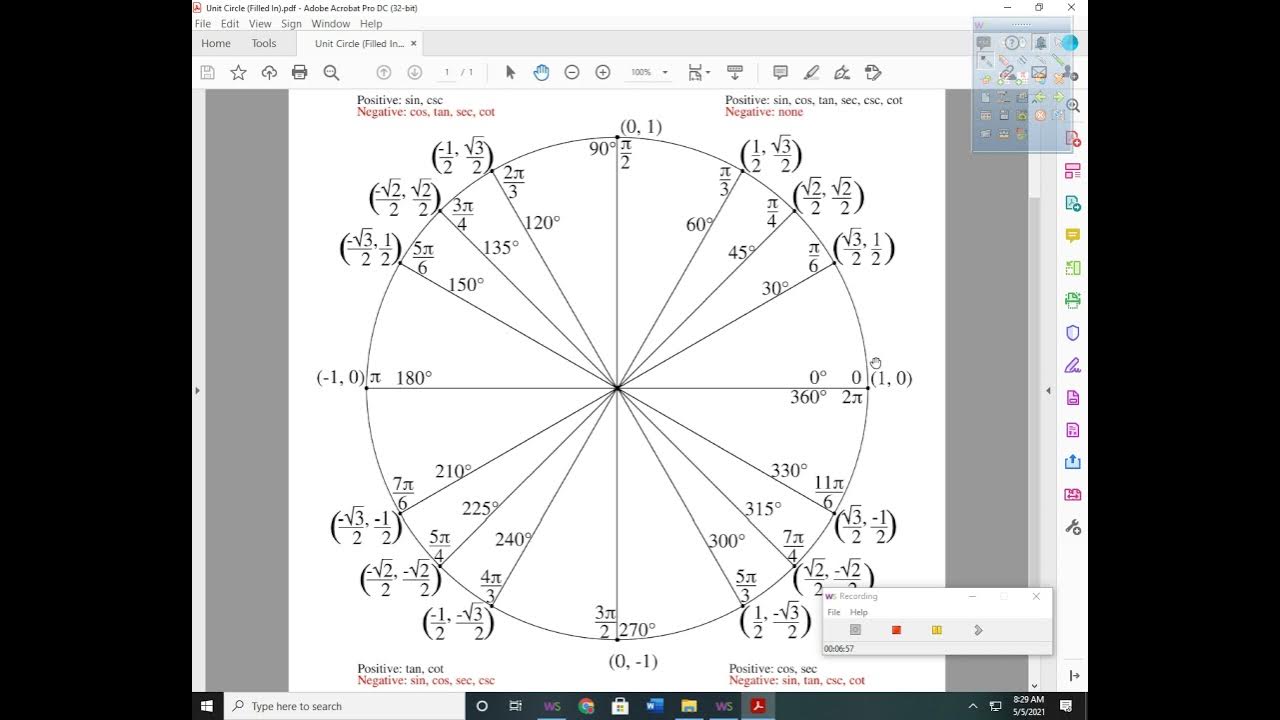
- 📐 The unit circle is referenced as a tool for finding the values of cosine and sine at specific angles, especially when dealing with angles that result in known values on the unit circle.
- 📝 Emphasis is placed on the practical application of these identities in calculus and other areas of mathematics where breaking down products into sums can simplify complex problems.
Q & A
What are the sum-to-product and product-to-sum formulas used for?
-The sum-to-product and product-to-sum formulas are used to transform trigonometric expressions involving the sum or difference of angles into products or sums of trigonometric functions. This can simplify calculations and make it easier to solve certain mathematical problems.
How do you derive the product-to-sum formula for cosine of two different angles?
-You can derive the product-to-sum formula for cosine by adding the sum and difference formulas for cosine (cos(α + β) and cos(α - β)) and then simplifying the resulting expression. The terms involving the product of sines cancel out, leaving you with an expression involving the product of cosines.
What is the product-to-sum formula for sine and cosine of two different angles?
-The product-to-sum formula for sine and cosine of two different angles is given by: sin(α)cos(β) = 1/2 [sin(α + β) + sin(α - β)].
Why is it important to maintain the order of angles when using the sum-to-product formulas?
-Maintaining the order of angles is important because the trigonometric functions are not commutative. The order in which angles are added or subtracted affects the final result, especially when dealing with sine functions, which are odd functions.
How can you simplify the expression cos(3θ)cos(4θ) using the product-to-sum formulas?
-You can simplify the expression cos(3θ)cos(4θ) by using the formula for the product of cosines of two different angles, which results in 1/2 [cos(3θ + 4θ) + cos(3θ - 4θ)], and then simplifying to 1/2 [cos(7θ) + cos(-θ)].
What is the significance of the zero product property in solving trigonometric equations?
-The zero product property states that if a product of factors equals zero, then at least one of the factors must be zero. This property is significant in solving trigonometric equations because it allows you to set each factor equal to zero and solve for the variable, making it easier to find the solutions.
Why is it useful to convert a sum of trigonometric functions into a product?
-Converting a sum into a product is useful because products can be factored, which allows you to use the zero product property to find solutions to equations. This is particularly helpful when solving trigonometric equations involving different angles.
What is the sum-to-product formula for the sine of two different angles?
-The sum-to-product formula for the sine of two different angles is given by: sin(α) + sin(β) = 2sin((α + β)/2)cos((α - β)/2).
How can you use the product-to-sum formulas to find the exact value of sin(285°)sin(75°)?
-You can use the product-to-sum formula for sine by substituting the given angles into the formula, which results in 1/2 [cos(285° - 75°) - cos(285° + 75°)]. Then, by evaluating the cosines for the resulting angles (210° and 360°), you can find the exact value of the original expression.
What is the key difference between sine and cosine functions when it comes to changing the sign of the angle?
-The key difference is that sine is an odd function, meaning that changing the sign of the angle will also change the sign of the sine function. Cosine, on the other hand, is an even function, so changing the sign of the angle does not change the sign of the cosine function.
Why is it not possible to simplify sin(4θ)cos(6θ) further using basic trigonometric identities?
-It is not possible to simplify sin(4θ)cos(6θ) further using basic trigonometric identities because there are no identities that allow you to combine or factor out terms when you have a sine and cosine function of different angles without additional information or relationships between the angles.
Outlines
📚 Introduction to Sum and Product Formulas
The video begins with an introduction to sum and product formulas, focusing on their application in transforming products of trigonometric functions into sums and vice versa. The presenter assures viewers that the formulas are not complex and will be demonstrated through examples to ensure understanding. The goal is to transition into using these formulas to prove certain identities and solve equations, particularly those involving sine and cosine functions.
🔍 Proving Product-to-Sum Formulas
The presenter delves into proving the product-to-sum formulas using the sum and difference formulas for sine and cosine. By adding and subtracting these formulas, parts of the equation cancel out, allowing the presenter to solve for a product that can be expressed as a new identity. This process is demonstrated step by step for cosine and sine functions, resulting in the first two product-to-sum formulas.
🌟 Product-to-Sum Formulas for Sine and Cosine
The video continues with the derivation of the remaining product-to-sum formulas, specifically for sine and cosine products. The presenter shows that multiplication's commutative property means that finding a sine-cosine formula is sufficient, eliminating the need for a cosine-sine formula. The resulting formulas allow the transformation of products of sines, cosines, and sine-cosine into sums, which simplifies many mathematical operations.
📝 Applying Product-to-Sum Formulas
The presenter demonstrates the application of the product-to-sum formulas with examples involving angles not on the unit circle. By using these formulas, complex trigonometric expressions can be simplified or transformed into more manageable forms. The video covers examples of finding exact values for products of sine and cosine functions for various angles, showcasing the utility of the formulas in trigonometry.
🔢 Simplifying Sums into Products
The focus shifts to the reverse process of converting sums into products using new formulas. The presenter explains that this conversion is beneficial for solving equations, as products can be factored, a technique not available for sums. Examples are provided to illustrate how to apply these formulas, emphasizing the importance of maintaining the correct order when adding or subtracting angles.
🧮 Sum-to-Product Formulas with Examples
The presenter works through several examples using the sum-to-product formulas, showing how to simplify expressions involving sine and cosine functions with different angles. The importance of using identities for trigonometric functions is highlighted, as well as the need to follow the correct order when applying the formulas. The video demonstrates how to handle negative angles and the use of even and odd function properties to simplify expressions.
🔍 Solving Equations Using Sum and Product Formulas
The video concludes with an explanation of why converting sums to products is particularly useful for solving equations. The presenter uses the zero product property to solve equations involving sine functions with different angles. By transforming sums into products, the presenter sets each factor equal to zero, providing solutions to the equation. The utility of sum-to-product formulas in making complex equations solvable is emphasized.
🎓 Summary and Final Thoughts
In the final paragraph, the presenter summarizes the key points covered in the video, including the importance of sum and product formulas in trigonometry and their application in solving equations. The presenter expresses hope that the content is helpful and encourages viewers to practice the concepts on their own. The video ends on a positive note, wishing viewers a great day.
Mindmap
Keywords
💡Sum to Product Formulas
💡Product to Sum Formulas
💡Trigonometric Functions
💡Unit Circle
💡Zero Product Property
💡Sine Function
💡Cosine Function
💡Angles
💡Odd and Even Functions
💡Simplification
💡Substitution
Highlights
The video discusses the product to sum and sum to product formulas, providing a deeper understanding of their applications in mathematics.
The product to sum formulas are proven using the sum and difference formulas for sine and cosine, demonstrating the process of canceling parts of equations to solve for products.
The video provides a clear explanation of how to convert products of sine and cosine functions into sums, and vice versa, which is crucial for advanced mathematical concepts.
The importance of order when adding or subtracting angles in trigonometric functions is emphasized, as it affects the final outcome of the equations.
The video includes practical examples of using the product to sum formulas, showing how they can simplify complex trigonometric expressions into more manageable forms.
The concept of using identities to change angles in trigonometric functions is introduced, which is essential for solving problems that involve non-unit circle angles.
The video explains how the properties of sine and cosine as odd and even functions, respectively, influence the signs of the results when changing angles in trigonometric expressions.
The process of solving trigonometric equations using the sum to product formulas is demonstrated, highlighting their utility in breaking down complex problems into simpler, solvable parts.
The video emphasizes the importance of using the correct formulas when dealing with sums and products of different trigonometric functions, such as sine and cosine.
The concept of simplification of trigonometric expressions is discussed, showing how to deal with complex fractions and maintain the integrity of the mathematical relationships.
The video provides a comprehensive overview of the product to sum and sum to product formulas, their proofs, and their applications in solving trigonometric problems.
The role of the unit circle in understanding and solving trigonometric problems is introduced, preparing viewers for further studies in right triangle trigonometry.
The video concludes with a discussion on the practical applications of the formulas in solving equations, showcasing their importance in mathematical problem-solving.
The video is designed to ensure understanding of the material, ending with a summary of key formulas and their applications in trigonometry.
Transcripts
Browse More Related Video

Introduction to Sum and Difference Formulas in Trigonometry (Precalculus - Trigonometry 25)
5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Ultimate trig identity problem study guide!

Using Sum and Difference Formulas in Trigonometry (Precalculus - Trigonometry 26)

Sum and Difference Identities of Sine and Cosine

Trig Identities
5.0 / 5 (0 votes)
Thanks for rating: