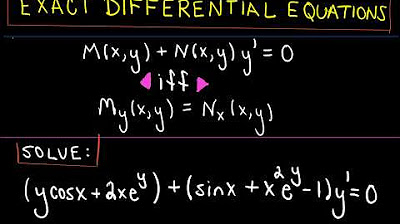What are Exact Differential Equations (Differential Equations 28)
TLDRThis video delves into the concept of exact differential equations, explaining their origin, application, and the process of solving for the potential function that generates level curves. The importance of mixed partial derivatives being equal for a function to be continuous and differentiable is highlighted. Two methods for solving exact differential equations are introduced, along with the necessity of conducting a test to verify if a given equation is exact. The video aims to clarify the logic behind these mathematical concepts and provides a step-by-step approach to solving related problems.
Takeaways
- 📚 The concept of exact differential equations is introduced, which are derived from potential functions and involve level curves in multivariable calculus.
- 🔍 Exact differential equations are identified by checking if the mixed partial derivatives of the given function are equal. This is a necessary condition for the function to be continuous and differentiable over a region.
- 🌐 The process of solving an exact differential equation involves integrating one of the partial derivatives with respect to the corresponding variable and then taking a derivative with respect to the other variable to find the missing function.
- 📈 The total differential form of a function is represented as M(dX) + N(dY) = 0, where M and N are the partial derivatives of the function F with respect to X and Y, respectively.
- 🧩 To verify if a given equation is an exact differential, one must perform a test checking if ∂M/∂Y = ∂N/∂X. If this condition is met, the equation is an exact differential for some potential function.
- 🔄 The method for solving an exact differential equation involves two steps: first, integrating the partial derivative with respect to one variable, and second, taking a derivative with respect to the other variable to find the function's missing part.
- 💡 It is not necessary to perform an integration with respect to both variables; only one integration and one derivative are needed to find the potential function.
- 🎯 The goal when solving an exact differential equation is to find the potential function F, which when set equal to a constant, produces the level curves of the original function.
- 📌 The process of solving an exact differential equation can be visualized as going from the differential form back to the potential function, using integration and derivatives as the primary mathematical tools.
- 🔑 The script emphasizes the importance of understanding the underlying concepts and the logical steps involved in solving exact differential equations, rather than just memorizing the process.
Q & A
What is the main topic of the video?
-The main topic of the video is about exact differential equations, their origin, usage, and the process of solving for the potential function that gives the exact difference equation.
What are level curves and how do they relate to surfaces in multivariable calculus?
-Level curves are curves on a plane that result when a function of two variables is set equal to a constant. They relate to surfaces in multivariable calculus as they represent the intersections of a 3D surface with a plane parallel to the coordinate plane, where the function's value is constant.
How can you determine if a given differential equation is exact?
-To determine if a differential equation is exact, you need to check if the mixed partial derivatives of the function are equal. If the partial derivative of M with respect to Y is equal to the partial derivative of N with respect to X, then the equation is exact.
What is the significance of the term 'exact differential' in the context of the video?
-An exact differential refers to a differential that is derived from a potential function. This means that the differential equation represents the level curves of a function that is continuous and differentiable over a certain region.
What is the process for solving an exact differential equation?
-The process involves first checking if the given differential equation is exact by comparing the mixed partial derivatives. If it is exact, one can then integrate with respect to one of the variables (X or Y), take a derivative with respect to the other variable, and solve for the unknown function, ultimately finding the potential function that describes the original differential equation.
What is the role of calculus 3 in understanding exact differential equations?
-Calculus 3 provides the foundational knowledge of multivariable functions, their differentials, and level curves, which are essential for understanding the concepts of exact differential equations and their solutions.
How do you find the potential function from an exact differential equation?
-To find the potential function, you first integrate one of the partial derivatives (with respect to either X or Y) to get a function of the other variable. Then, you take a derivative of this function with respect to the remaining variable and set it equal to the corresponding other partial derivative. Solving this gives you the missing function, and the sum of these two functions is the potential function.
What is the practical importance of level curves in physics and engineering?
-Level curves are significant in physics and engineering as they often represent physical or system properties that are constant, such as pressure or temperature in a fluid, or potential in an electrical field. Understanding these curves helps in analyzing and solving real-world problems.
What happens if the mixed partial derivatives are not equal?
-If the mixed partial derivatives are not equal, the differential equation is not exact for some potential function in the given region. In such cases, an integrating factor may be used to transform the non-exact differential equation into an exact one.
How does the concept of a potential function relate to exact differential equations?
-A potential function is related to exact differential equations because it provides a way to express the differential equation as the total differential of a function. This is only possible if the differential equation is exact, meaning the mixed partial derivatives are equal.
Outlines
📘 Introduction to Exact Differential Equations
The video begins with an introduction to exact differential equations, explaining their origin and applications. The concept is linked to calculus, specifically multivariable functions and level curves. The speaker aims to clarify what exact differential equations are, their derivation, and the process of solving them to find the potential function that leads to these equations.
📚 Derivation and Properties of Exact Differential Equations
The speaker delves into the derivation of exact differential equations, highlighting two methods for obtaining the same result. The first method involves implicit differentiation, while the second uses partial derivatives. The importance of understanding the underlying potential function and the conditions under which a differential equation is considered exact is emphasized, with a focus on the equality of mixed partial derivatives as a key criterion.
🔍 Testing for Exactness: The Method of Mixed Partials
The paragraph explains the process of testing whether a given differential equation is exact by comparing the mixed partial derivatives. If these derivatives are equal, the equation is exact and can be traced back to a potential function. The speaker outlines the steps for this test and sets the stage for solving the equation by integrating and finding the missing function components.
📈 Solving Exact Differential Equations: Techniques and Examples
The speaker presents techniques for solving exact differential equations, including the use of integration and partial derivatives. Two methods are discussed: integrating with respect to the variable associated with the partial derivative and then taking a derivative with respect to the other variable. The speaker provides examples to illustrate these techniques, emphasizing the importance of understanding the process and the underlying mathematical principles.
📊 Further Exploration of Solving Exact Differential Equations
Continuing from the previous paragraph, the speaker further explores the process of solving exact differential equations. They provide additional examples and reiterate the steps involved in finding the potential function. The speaker also discusses the concept of integrating factors for non-exact differential equations, setting the stage for further discussion in subsequent videos.
🎓 Summary and Understanding of Exact Differential Equations
The speaker summarizes the key points covered in the video, emphasizing the importance of understanding the meaning and origin of exact differential equations. They stress the necessity of performing the mixed partials test before attempting to solve the equation and highlight the process of integrating and differentiating to find the potential function. The speaker aims to ensure that viewers have a clear and comprehensive understanding of the topic.
Mindmap
Keywords
💡Exact Differential Equations
💡Level Curves
💡Partial Derivatives
💡Potential Function
💡Mixed Partial Derivatives
💡Implicit Differentiation
💡Total Differential
💡Surfaces in R^3
💡Differential Forms
💡Integration
Highlights
The video discusses exact differential equations, their origins, and their applications in physics and engineering.
Exact differential equations are related to level curves, which are surfaces set equal to a constant.
The concept of exact differential equations is derived from calculus 3, specifically from multivariable functions.
The total differential for a potential function is represented as the partial derivative of F with respect to X times DX plus the partial derivative of F with respect to Y times DY.
Implicit differentiation can be used to derive the differential equation from a level curve.
Exact differential equations are important for solving problems involving potential functions and level curves.
Mixed partial derivatives are equal for functions that are continuous and differentiable, which is a key test for exact differential equations.
The process of solving exact differential equations involves integrating and finding the potential function that gives rise to the level curves.
The video provides a step-by-step method for determining if a given equation is an exact differential equation and how to solve it.
Two techniques for solving exact differential equations are presented, one involving integration with respect to X and the other with respect to Y.
The video emphasizes the importance of checking mixed partials before attempting to solve an exact differential equation.
The solution to an exact differential equation results in a family of curves, with initial values used to find specific solutions.
The video demonstrates that the choice between integrating with respect to X or Y does not affect the final solution.
The process of solving exact differential equations can be simplified by choosing the easier integral to perform first.
The video concludes with a promise to provide more examples and practice in the next installment.
The importance of understanding the theoretical underpinnings of exact differential equations is emphasized for truly grasping the concept.
The video aims to clarify common misconceptions and provide a comprehensive understanding of exact differential equations.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: