Solving Differential Equations with Embedded Derivative Substitutions (Differential Equations 24)

Professor Leonard

11 Dec 201847:31

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the technique of embedded derivatives for solving first-order differential equations. The method involves identifying a piece of the equation that is a derivative of another piece containing 'y', and substituting it to simplify the equation. The technique is powerful when it fits, making difficult equations manageable, though it doesn't always result in linear equations. The script provides detailed examples and emphasizes the importance of recognizing when to apply this method among other techniques.

Takeaways

📚 The embedded derivatives technique is a method for solving first-order differential equations by identifying a piece of the equation that is a derivative of another piece.
🔍 To apply this technique, look for a function of Y that is the derivative of another function present in the differential equation.
🧠 The process involves making a substitution to rewrite the differential equation in terms of a new function V, which simplifies the equation and often leads to a linear form.
🎯 The key is to find a piece that includes a Y and is a derivative of another piece; this allows for the application of the chain rule and simplification.
📈 The technique is particularly useful when other methods like homogeneous or Bernoulli equations are difficult or complex to apply.
🚫 Note that embedded derivatives do not always result in linear equations and may require additional techniques like homogeneous transformations for certain types of equations.
🤝 The substitution process involves two main steps: first, replacing the Y-related terms with V, and then solving for the new dependent variable V before converting back to Y.
🌟 The power of the embedded derivatives technique lies in its ability to simplify complex differential equations into more manageable forms.
📊 When applying the technique, be aware of potential domain restrictions, especially when dealing with linear equations and integrating factors.
🔄 The process may involve multiple substitutions, and always remember to revert back to the original variable Y after solving for V.
🔑 The embedded derivatives technique is a valuable tool in the solver's arsenal, offering a fresh approach to tackling difficult differential equations.

Q & A

What is the embedded derivatives technique used for in solving differential equations?
-The embedded derivatives technique is used for solving first-order differential equations by identifying a piece of the equation that is a derivative of another piece, allowing for a substitution that can simplify the equation into a more manageable form, such as linear or separable.
What are the key features of a differential equation that suggest the use of the embedded derivatives technique?
-The key features include the presence of a piece of the equation that is a derivative of another piece, and that the derivative is connected to the differential term dy/dx by multiplication. This technique is particularly useful when the equation does not fit neatly into other common forms like linear, separable, or Bernoulli equations.
How does the embedded derivatives technique involve substitution?
-The embedded derivatives technique involves substituting the function that is not the derivative (V) with its derivative (dy/dx or DV DX), effectively replacing the entire function with DV DX. This substitution simplifies the differential equation and can transform it into a form that is easier to solve.
What is the role of the chain rule in the embedded derivatives technique?
-The chain rule plays a crucial role in the embedded derivatives technique as it allows us to express the derivative of a function in terms of the derivative of its components. Specifically, when we substitute the function V with its derivative DV DX, the chain rule ensures that the dy/dx term is accounted for in the new form of the differential equation.
Can the embedded derivatives technique always result in a linear differential equation?
-No, the embedded derivatives technique does not always result in a linear differential equation. While it can simplify the original equation into a form that is more amenable to solution techniques, the outcome depends on the structure of the original equation and whether it can be transformed into a linear form through the substitution process.
What is the significance of domain restrictions in the context of the embedded derivatives technique?
-Domain restrictions are significant because they ensure that the solutions obtained from the differential equations are valid for all values of the independent variable (usually x). For example, in linear differential equations, we often divide by x, which implies that x cannot be zero. Domain restrictions help us define the range of values for the variables that make sense within the context of the problem.
How does the embedded derivatives technique handle terms that are not part of the derivative in the differential equation?
-Terms that are not part of the derivative are treated as separate entities in the embedded derivatives technique. They are not replaced with DV DX and remain in their original form. The goal is to isolate and simplify the derivative-related terms, which can then be solved more easily, while the non-derivative terms are carried along in the equation.
What is the process for reverting back to the original variable after using the embedded derivatives technique?
-After solving the simplified equation obtained through the embedded derivatives technique, we revert back to the original variable by substituting the derived function V back into the solution for the variable y. This is done by replacing V with its original expression in terms of y, effectively reversing the initial substitution.
Can you provide an example of a differential equation that is not suitable for the embedded derivatives technique?
-An example of a differential equation that may not be suitable for the embedded derivatives technique is one where the derivative term dy/dx is not connected to another piece of the equation by multiplication, or where there is no clear piece of the equation that is a derivative of another piece. For instance, an equation like dy/dx + P(x)y = Q(x)sin(y) would not fit the criteria for the embedded derivatives technique.
What is the advantage of using the embedded derivatives technique over other methods for solving differential equations?
-The advantage of using the embedded derivatives technique is that it can simplify complex differential equations into more straightforward forms, such as linear or separable equations, which are easier to solve. This technique can save time and effort, especially when dealing with equations that do not fit neatly into other common forms and would require more complex manipulations or transformations using other methods.

Outlines

00:00

📚 Introduction to Embedded Derivatives

The paragraph introduces the concept of embedded derivatives, a technique for solving first-order differential equations. It emphasizes that while multiple techniques may exist for solving a single equation, embedded derivatives stand out for their innovative approach. The technique involves identifying a piece of the differential equation that is a derivative of another piece, including a variable 'y'. The goal is to simplify the equation by rewriting it in terms of a new function 'V', which represents the identified derivative piece. The method is particularly useful when other techniques like homogeneous or Bernoulli equations prove challenging.

05:02

🔍 How to Identify Embedded Derivatives

This section delves into the specifics of identifying embedded derivatives within a differential equation. It explains the process of looking for a function of 'y' that, when differentiated, is also present in the equation. The speaker illustrates this by choosing a function 'V' such that its derivative appears in the equation. The derivative of 'V' is then used to replace the 'dy/dx' term through a substitution, which can significantly simplify the equation. The paragraph also cautions that this technique is not universally applicable, as not all equations will contain the necessary derivative relationships.

10:05

📈 Example Walkthrough: Solving with Embedded Derivatives

The speaker provides a step-by-step example of solving a differential equation using embedded derivatives. The example demonstrates how to identify the piece of the equation that is a derivative of another piece and how to perform the substitution to rewrite the equation in terms of 'V'. The process leads to a linear differential equation in terms of 'V' and 'x', which can then be solved using integrating factors. The paragraph highlights the power of this technique in transforming complex equations into more manageable forms.

15:07

🧩 Putting the Pieces Back: Returning to 'y'

After solving the differential equation in terms of 'V', the speaker explains how to revert back to the original variable 'y'. This involves using the substitution made earlier to express 'V' in terms of 'y'. The process is likened to other substitution techniques such as homogeneous or Bernoulli, where a function of 'y' is reintroduced to find the final solution. The paragraph emphasizes the importance of this step in fully solving the differential equation.

20:07

📊 Further Examples and Technique Application

The speaker presents additional examples to reinforce the application of the embedded derivatives technique. These examples illustrate the versatility of the method in solving a variety of differential equations that may not conform to standard forms. The paragraph also hints at a future video where the speaker plans to revisit five challenging problems, showcasing how the embedded derivatives technique can simplify their solutions.

25:09

🔧 Working with Non-Linear Equations

This paragraph discusses the application of embedded derivatives in non-linear differential equations. The speaker acknowledges that not all equations will result in linear equations after applying the technique, but it can still be a valuable tool. The example provided walks through the process of identifying the correct piece for substitution and transforming the equation into a more recognizable form, such as linear or separable, even if it doesn't result in a linear equation.

30:10

🌟 Final Thoughts on Embedded Derivatives

The speaker concludes the discussion on embedded derivatives by reiterating its utility in solving differential equations. The technique is presented as a powerful tool that, when applicable, can greatly simplify the process of finding solutions. The speaker encourages viewers to recognize the potential of this method and to apply it when they encounter equations that fit the criteria for embedded derivatives.

Mindmap

Keywords

💡First-order differential equations

First-order differential equations refer to equations that involve the first derivative of an unknown function. In the context of the video, these equations are the primary focus, and the speaker introduces techniques for solving them, emphasizing that multiple methods may exist for a single equation.

💡Embedded derivatives

Embedded derivatives is a technique for solving certain types of first-order differential equations. It involves identifying a part of the equation that is a derivative of another part. This technique requires a deep understanding of the structure of the differential equation to recognize and manipulate the terms effectively.

💡Substitution

Substitution is a mathematical method used to simplify expressions or equations by replacing certain terms with other variables or expressions. In the context of the video, substitution is a crucial step in the embedded derivatives technique, where specific parts of the differential equation are replaced with new variables to facilitate easier solving.

💡Derivative

A derivative is a mathematical concept that represents the rate of change of a function with respect to its independent variable. In differential equations, finding the derivative of a function is often necessary to express the relationship between variables and to solve the equation.

💡Chain rule

The chain rule is a fundamental principle in calculus that is used to find the derivative of a composite function. It states that the derivative of a function that is the result of other functions is the product of the derivatives of each function in the chain.

💡Linear differential equations

Linear differential equations are a class of differential equations where the dependent variable and its derivatives appear only to the first power and are linearly combined. These equations are easier to solve compared to nonlinear equations and often have unique solutions.

💡Integrating factor

An integrating factor is a function used in the solution of linear differential equations to simplify the equation into an exact differential equation, which can then be integrated. It is a crucial concept in solving first-order linear differential equations.

💡Homogeneous differential equations

Homogeneous differential equations are a type of linear differential equation where all terms involving the dependent variable and its derivatives are of the same degree. They can often be solved using specific techniques that take advantage of their homogeneous nature.

💡Bernoulli differential equations

Bernoulli differential equations are a special class of nonlinear differential equations that can be transformed into a linear form by a substitution. They are named after the Swiss mathematician Johann Bernoulli, who introduced them in the 17th century.

💡Domain restrictions

Domain restrictions refer to the set of allowable values for the independent variable in a function or equation. These restrictions are necessary when certain operations, such as division by zero or taking the square root of a negative number, would lead to undefined or complex results.

Highlights

The introduction of the embedded derivatives technique for solving first-order differential equations.

The technique's ability to simplify differential equations by identifying a piece that is a derivative of another piece within the equation.

The requirement for the identified piece to include a 'y' and be connected to 'dy/dx' by multiplication.

The process of rewriting the differential equation by replacing the identified piece with 'DV/DX' and the remaining piece with 'V'.

The use of chain rule when taking derivatives to clear up the differential equation.

The potential for the technique to simplify problems that are difficult to solve using other methods like Bernoulli or homogeneous equations.

The example provided to illustrate the technique, where 'y^3' is identified as the embedded derivative and replaced with 'V'.

The transformation of the differential equation into a linear form by dividing by 'x' and identifying 'P(x)' for the integrating factor.

The use of integrating factors to solve linear differential equations and the importance of domain restrictions.

The step-by-step solution of the example equation, leading to the final form 'e^(x) * B = x + C'.

The process of reverting back to 'y' from 'V' by using the substitution technique twice.

The explanation of potential domain issues, especially with linear differential equations involving division.

The mention of upcoming examples that will demonstrate the technique's utility and compare it with other methods.

The emphasis on the embedded derivatives technique as a powerful method for solving certain types of differential equations.

The final example involving 'sin^2(y)' and the process of making the differential equation look more linear.

The conclusion that not all embedded derivative substitutions result in linear equations, and the possibility of using other techniques.

Transcripts

Browse More Related Video

How Embedded Derivatives Can Make Differential Equations Easier (Differential Equations 25)

Introduction to Linear Differential Equations and Integrating Factors (Differential Equations 15)

Linear Differential Equations & the Method of Integrating Factors

How to Solve Bernoulli Differential Equations (Differential Equations 23)

Reducible Second Order Differential Equations, Missing Y (Differential Equations 26)

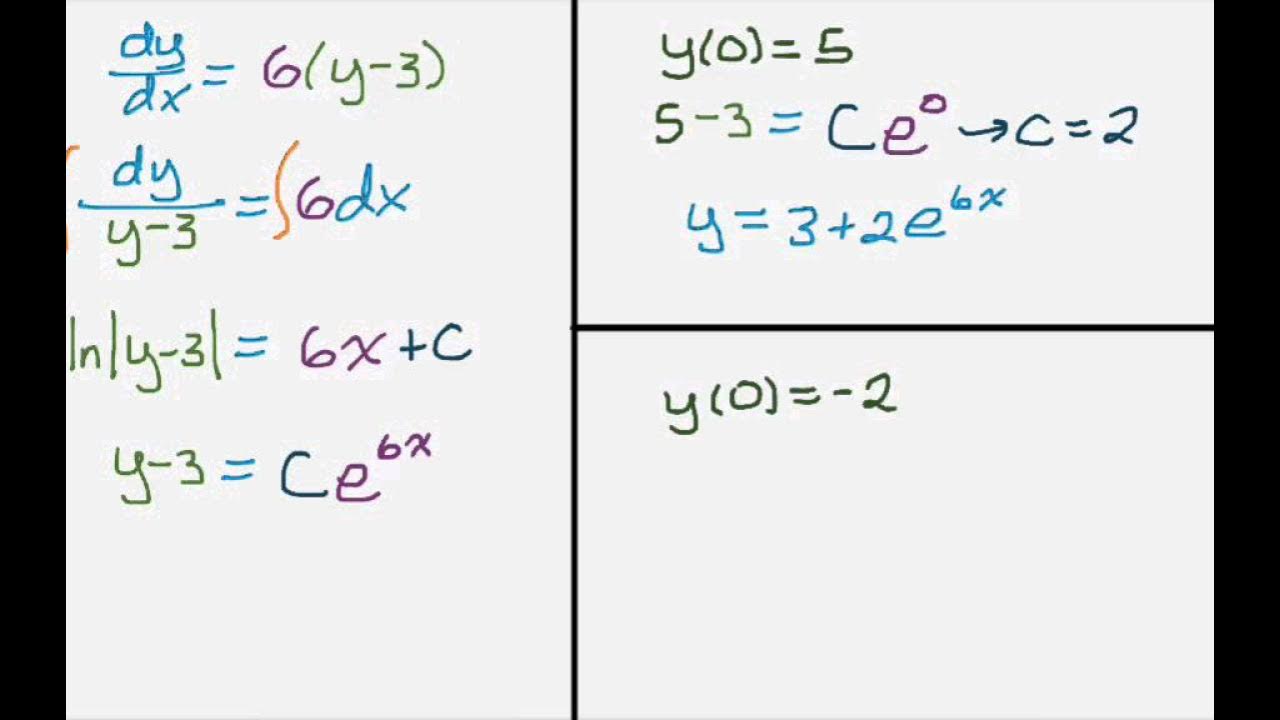
Separable Differential Equation (Natural Logs)

Related Tags

Differential Equations Embedded Derivatives Mathematical Techniques Bernoulli Equations Homogeneous Equations Integration Methods Linear Equations Substitution Techniques Math Education Problem Solving