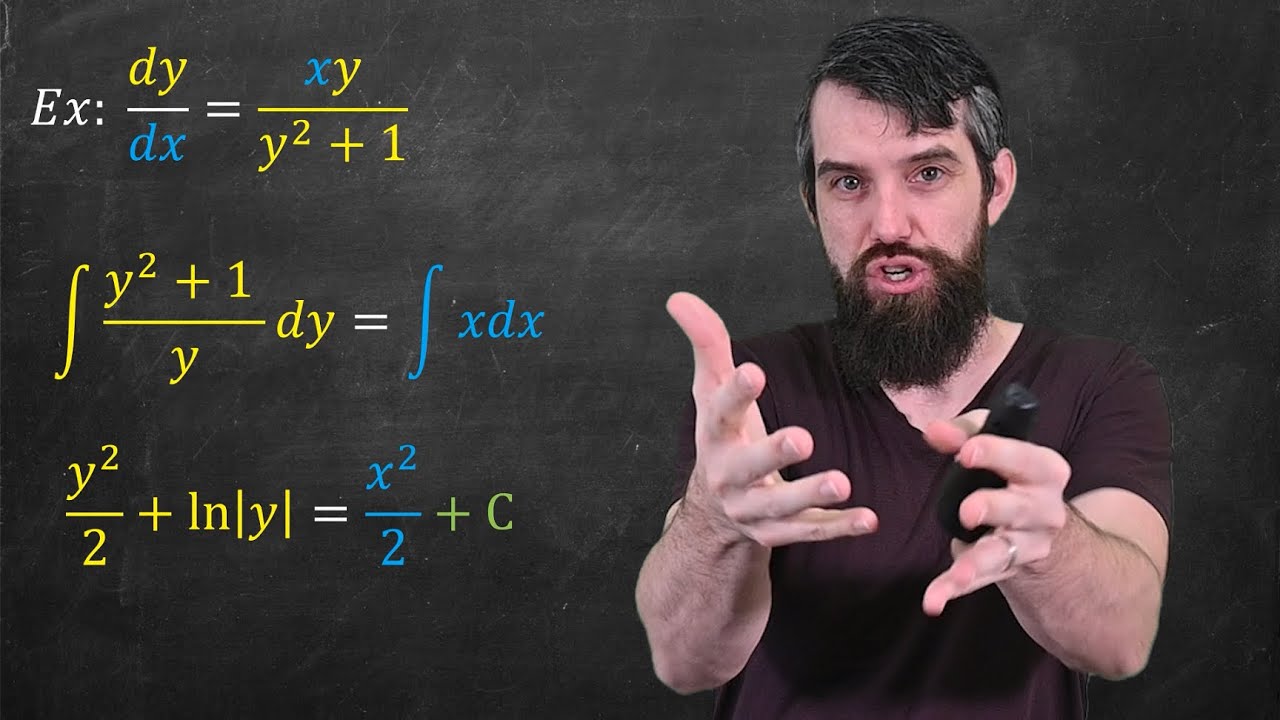Separable Differential Equations (Differential Equations 12)
TLDRThe video script discusses the technique of solving first-order differential equations through separation of variables. It emphasizes the importance of recognizing when a differential equation is separable and outlines the steps for separating variables, integrating both sides, and solving for the dependent variable. The script provides numerous examples to illustrate the process, highlighting the use of integration techniques and the handling of arbitrary constants. It also introduces the concept of singular solutions, which may not be captured by the general solution and require alternative methods for identification.
Takeaways
- 📚 Differential equations are equations that involve derivatives, and understanding them is crucial in various fields of mathematics and physics.
- 🔍 The process of solving first-order differential equations often involves identifying if they are separable, meaning the equation can be written as a product of functions of x and y.
- 🧠 Separation of variables is a fundamental technique where you rearrange the equation so that all y-terms and dy are on one side, and x-terms and dx are on the other.
- 🌟 Integrals play a key role in solving differential equations since integrating both sides of the separated equation can lead to the solution.
- 📈 When integrating, it's important to keep coefficients and constants on the same side to simplify the process and ensure the correct matching of variables after integration.
- 🤔 Sometimes, the general solution to a differential equation may not include all possible solutions, such as singular solutions, which require separate identification.
- 📊 The script provides numerous examples to illustrate the process of separating variables and integrating to solve differential equations, emphasizing the importance of practice.
- 🛠️ The method of partial fractions is mentioned as a useful technique for certain types of differential equations that do not lend themselves easily to direct separation of variables.
- 📝 It's crucial to verify solutions by plugging them back into the original differential equation to ensure they satisfy the equation.
- 🎓 The video script serves as a comprehensive guide for learners to understand the concepts and techniques involved in solving first-order differential equations by separation of variables.
Q & A
What is the main technique discussed in the transcript for solving differential equations?
-The main technique discussed is the separation of variables, also known as separable equations, where the equation can be rearranged so that all terms involving 'y' are on one side and all terms involving 'x' are on the other side, allowing for integration to solve the equation.
What is the significance of the integral in solving differential equations?
-Integrals are crucial in solving differential equations because they can 'undo' a derivative, effectively finding the antiderivative or the parent function that satisfies the differential equation. This is particularly useful when dealing with basic differential equations where an integral can directly solve for the function 'y'.
What is the first step in using the separation of variables technique?
-The first step is to identify if the differential equation is in a form that allows for separation of variables, meaning it can be written as dy/dx = f(y)g(x), where 'f(y)' and 'g(x)' are functions of 'y' and 'x' respectively.
What are some of the other techniques mentioned for solving first-order differential equations?
-Other techniques mentioned include homogeneous differential equations, Bernoulli equations with substitution, and linear differential equations. These are alternative methods for solving differential equations when the separation of variables technique is not applicable or convenient.
Why is it important to keep constants on the same side of the equation when separating variables?
-Keeping constants on the same side simplifies the process of solving for 'y'. If constants are moved to the 'y' side, it can make the equation more complex and difficult to solve, especially when integrating.
What happens when you integrate both sides of a differential equation?
-When you integrate both sides of a differential equation, you effectively find the antiderivative or the parent function for 'y'. This results in an equation that, when differentiated, will yield the original differential equation, thus providing a solution.
What is the role of the arbitrary constant 'C' in the general solution of a differential equation?
-The arbitrary constant 'C' represents the family of solutions to the differential equation. It accounts for the fact that there can be infinitely many solutions, each differing by a constant value, which is not determined by the differential equation itself.
How does the process of separating variables apply to the example of dy/dx = -2x?
-In the example of dy/dx = -2x, the 'y' terms are already isolated on one side, allowing for direct integration. The left side becomes an integral with respect to 'y', yielding ln|y|, and the right side becomes an integral with respect to 'x', yielding -x^2. After integrating, the general solution is found by combining these results.
What is a singular solution in the context of differential equations?
-A singular solution is a solution that does not appear in the general solution derived from the separation of variables technique. These solutions can only be found by other methods, such as guess and check or by analyzing specific conditions that satisfy the differential equation.
Why is it important to verify the solutions of a differential equation?
-Verification is important to ensure that the solutions satisfy the original differential equation. This is done by substituting the proposed solutions back into the differential equation to confirm that they indeed make the equation hold true.
Outlines
📚 Introduction to Solving Differential Equations
The paragraph introduces the concept of solving differential equations, emphasizing the excitement of learning the first technique. It discusses the importance of understanding differential equations, slope fields, and approximations. The speaker mentions that while integrals can solve basic differential equations, the video will focus on a more straightforward technique for first-order differential equations, highlighting the separation of variables as the key method.
📈 Separable Differential Equations
This paragraph delves into the specifics of separable differential equations, explaining the process of separating variables and integrating both sides to solve for 'y'. The speaker provides a recap of the process and emphasizes the importance of keeping coefficients on the same side for easier solving. The paragraph also touches on the concept of singular solutions, which may not appear in the general solution but are still valid.
🔢 Integrating Differential Equations
The speaker explains the fundamental idea behind integrating differential equations, focusing on the separation of 'Y' terms and 'X' terms. The process involves moving all 'Y' related terms to one side and 'X' related terms to the other, then integrating both sides. The speaker also discusses the importance of matching up variables after integration and the concept of arbitrary constants in the general solution.
🌟 Solving for 'y' Explicitly
This section discusses the process of solving for 'y' explicitly in separable differential equations. The speaker provides examples of how to manipulate the equation to isolate 'y', including handling absolute values and exponents. The paragraph emphasizes the use of integration techniques and the importance of recognizing when an equation can be separated into a product of 'X' and 'Y' functions.
📊 Applying Integration Techniques
The speaker continues to apply integration techniques to various differential equations, demonstrating how to group terms and perform integrations to find the general solution. The paragraph covers several examples, each highlighting different aspects of integration and algebraic manipulation to solve for 'y'. The speaker encourages viewers to practice these techniques to solidify their understanding.
🎓 Advanced Integration and Solutions
This paragraph covers more complex cases of differential equations, including those that may not initially appear separable. The speaker uses examples to illustrate how to identify and manipulate factors to make the equation separable. The section also touches on special cases like singular solutions, which may not be part of the general solution but are still valid solutions to the differential equation.
🔍 Factoring and Special Cases
The speaker discusses the use of factoring by grouping to solve certain differential equations that do not initially appear separable. The paragraph emphasizes thinking outside the box and recognizing patterns that can be factored to create a product, allowing for variable separation. The speaker also introduces the concept of singular solutions, which are not always evident in the general solution but are important to consider.
📖 Summary and Next Steps
In the concluding paragraph, the speaker summarizes the process of solving differential equations by separation of variables, highlighting the importance of recognizing when an equation can be separated and when it cannot. The speaker also mentions that while the general solution is powerful, it may not capture all solutions, such as singular solutions. The paragraph ends with a teaser for the next video, which will cover initial value problems and further techniques for solving differential equations.
Mindmap
Keywords
💡Differential Equations
💡Separable Differential Equations
💡Integrals
💡Slope Fields
💡First-Order Differential Equations
💡Anti-Derivative
💡Constants
💡General Solution
💡Partial Fractions
💡Substitution
💡Singular Solutions
Highlights
The introduction of the concept of solving differential equations using separation of variables.
Explanation of how integrals can solve differential equations due to the relationship between derivatives and integrals.
The importance of being able to rearrange the differential equation into a form where variables can be separated.
The method of moving all 'Y' terms and 'dy' to one side and 'X' terms and 'DX' to the other side for separation.
The process of integrating both sides of the equation after separating variables.
The necessity of keeping coefficients on the same side to simplify the solving process.
The concept of general solutions and the presence of an arbitrary constant 'C'.
The explanation of how to handle 'dy/dx' by treating it as a fraction and separating it.
The use of integration by parts and other techniques for more complex differential equations.
The introduction of the idea of singular solutions that do not appear in the general solution.
The method of solving for 'y' explicitly by using properties of logarithms and exponents.
The strategy of using substitution techniques for certain types of differential equations.
The process of using partial fractions to simplify the integration of complex fractions.
The approach of factoring by grouping to make a product out of seemingly non-separable terms.
The final step of solving for 'y' by applying inverse trigonometric functions when applicable.
The caution about potential singular solutions that may not be captured by the general solution method.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: