Solving Differential Equations with a Composition (Obvious) Substitution (Differential Equations 22)

Professor Leonard

20 Nov 201840:02

EducationalLearning

32 Likes 10 Comments

TLDRThis video tutorial delves into solving first-order differential equations using the technique of obvious substitutions. The presenter clarifies that 'obvious' does not always mean straightforward and guides viewers on how to identify compositions within equations to make effective substitutions. Through a series of examples, the video demonstrates how to transform complex equations into simpler, solvable forms by wrapping up variables in a function 'V', solving for 'y', and applying chain rule derivatives. The process aims to result in a separable equation, which can then be integrated for solutions. The video emphasizes the importance of recognizing compositions and the systematic approach to substitution and solving, highlighting its similarities with homogeneous equations.

Takeaways

🔍 The concept of 'obvious substitutions' is introduced as a method for solving differential equations that do not fit neatly into categories like homogeneous or Bernoulli equations.
🧠 Obvious substitutions involve looking for a composition of functions within the differential equation, which can be represented as 'V' to simplify the equation.
🔑 The process is similar to solving homogeneous equations, where a substitution is made, and the goal is to transform the equation into a separable form.
📈 The technique involves solving for 'y' in terms of 'V' and then taking a derivative to replace 'dy/dx' with a function of 'V' and 'x'.
🌟 A key aspect is ensuring that all 'y's are included in the 'V' composition and that 'dy/dx' is expressible as a derivative of 'V'.
📚 The video provides three examples to illustrate how to approach and apply obvious substitutions to different types of differential equations.
🛠️ The first example demonstrates how to handle a first-order differential equation with a composition of functions, leading to a separable equation that can be integrated.
📊 The second example shows a more complex scenario where the differential equation is not immediately solvable, requiring a substitution to simplify and then further manipulation to reach an implicit solution.
🔧 The third example involves a more intricate substitution process, highlighting the use of integration techniques and the importance of recognizing when an explicit solution is not feasible.
📐 The importance of recognizing 'obvious' compositions in differential equations is emphasized, as they are not always immediately apparent and require careful analysis.
🎯 The overall goal of obvious substitutions is to transform a complex differential equation into a more manageable form that can be solved using integration or other techniques.

Q & A

What is the main topic of the video?
-The main topic of the video is solving differential equations using obvious substitutions, focusing on identifying compositions within the equations and transforming them into separable or linear forms.
Why are obvious substitutions not always obvious?
-Obvious substitutions are not always obvious because the term 'obvious' in this context refers to identifying a composition within the differential equation that can be substituted to simplify the equation, which may not be immediately apparent to everyone.
What is a composition in the context of differential equations?
-A composition in the context of differential equations is a situation where one function is inside another, or in other words, it's a function of a function. This is typically what we look for when making obvious substitutions.
How does the technique of obvious substitutions relate to solving homogeneous equations?
-The technique of obvious substitutions is very similar to solving homogeneous equations. In both cases, a substitution is made to change the differential equation into a form that is either separable or linear, allowing the use of previously learned techniques or basic integrals.
What is the goal with substitutions in solving differential equations?
-The goal with substitutions in solving differential equations is to put the equation into a proper form, either a separable equation or a linear equation, by using a substitution that changes the structure of the equation, making it easier to solve.
How do you identify an obvious substitution in a differential equation?
-To identify an obvious substitution in a differential equation, look for a composition of functions that includes all the instances of the variable 'y'. This composition can then be replaced with a new variable 'V', and the equation can be solved for 'y' in terms of 'V'.
What is the process for solving a differential equation using an obvious substitution?
-The process involves identifying a composition in the equation, solving for 'y' in terms of this composition (now 'V'), taking the derivative of 'V', and replacing all 'y' terms and 'dy/dx' with the derivative of 'V'. This transforms the equation into a form that can be integrated to find the solution.
What happens when you can't solve for 'V' explicitly in an obvious substitution?
-When you can't solve for 'V' explicitly, you leave the solution in terms of 'V' and the other variables. You can then substitute back 'V' with the original composition to get an implicit solution for the differential equation.
How do you handle the 'dy/dx' term when making an obvious substitution?
-When making an obvious substitution, you need to find the derivative of the substitution, which replaces the 'dy/dx' term. This is because you can't have 'y' in the derivative form after the substitution; it must be expressed in terms of 'V'.
What is the significance of the chain rule in obvious substitutions?
-The chain rule is significant in obvious substitutions because when you take the derivative of 'V' with respect to 'x', you get a term that involves the derivative of the inner function (which is 'y' in the composition). This term is implicitly a chain rule, and it's crucial for correctly transforming the 'dy/dx' term in the substitution process.

Outlines

00:00

📘 Introduction to Obvious Substitutions in Differential Equations

The video begins with an introduction to solving differential equations using obvious substitutions, a technique that involves identifying a composition of functions within the equation. The speaker clarifies that 'obvious' does not always mean straightforward and provides three examples to illustrate the approach. The goal of substitutions is to transform the equation into a form that can be solved using known techniques or basic integrals. The first example focuses on identifying compositions within the equation and solving for y to replace dy/dx with a derivative of the substitution variable (V).

05:02

📙 Derivative Chain Rule and Substitution Application

This paragraph delves into the application of the chain rule and the process of substitution in solving differential equations. The speaker emphasizes the importance of wrapping all y terms in the substitution variable (V) and solving for y to facilitate the replacement of dy/dx. The process is likened to solving homogeneous equations, with the difference that the composition is not always y/x. The speaker demonstrates how to manipulate the equation to achieve a separable form, which can then be integrated to find the solution.

10:02

📙 Solving for V and Re-substitution

The speaker continues the example from the previous paragraph, showing how to solve for the substitution variable V and then re-substitute to find the solution in terms of x and y. The process involves using trigonometric substitution or an integration table to solve the separable equation. The speaker also highlights the importance of solving as much as possible for V before re-substituting to simplify the final steps and obtain the solution in terms of y and x.

15:03

📘 Deception in Obvious Substitutions

The speaker addresses the deceptive nature of the term 'obvious' in the context of substitutions, explaining that sometimes the substitutions are not immediately apparent. The focus shifts to looking for functions that can be substituted, such as square roots or denominators, which contain all y terms. The speaker encourages viewers to attempt obvious substitutions even if they are not immediately recognizable and provides an additional example to illustrate the concept.

20:03

📙 Tackling a Challenging Differential Equation

The speaker presents a more complex differential equation and explores the possibility of using obvious substitutions to simplify it. The equation does not lend itself to basic techniques or homogeneous forms, prompting the speaker to seek an alternative approach. The speaker identifies a composition in the equation and proceeds to solve for y, change dy/dx, and substitute to transform the equation into a separable form. The process involves dividing by V and grouping terms to facilitate separation of variables.

25:03

📙 Solving with Integration Techniques

In this paragraph, the speaker discusses the use of integration techniques to solve the transformed differential equation. The focus is on finding a common denominator and separating the equation into a product or quotient to integrate both sides. The speaker introduces a substitution with u=V+1 to simplify the equation further and demonstrates how to separate the terms into fractions for easier integration. The solution involves a combination of integrals and the use of natural logarithms.

30:04

📘 Final Steps and Implicit Solutions

The speaker concludes the video by discussing the final steps in solving the differential equation, emphasizing the challenge of solving for V explicitly and the alternative of leaving the solution implicit. The speaker demonstrates how to re-substitute the original variables x and y to obtain an implicit solution to the differential equation. The process involves careful handling of constants and the use of substitution to revert back to the original variables. The speaker also addresses the concept of arbitrary constants and their role in the final solution.

Mindmap

Keywords

💡Differential Equations

Differential equations are mathematical equations that involve an unknown function and its derivatives. In the context of the video, the focus is on first-order differential equations, which involve only the first derivative of the unknown function. The video discusses techniques for solving these equations, particularly through substitutions and transformations into more manageable forms.

💡Separation of Variables

Separation of variables is a method used to solve first-order differential equations. It involves rearranging the equation so that all the variables involving 'y' are on one side and all those involving 'x' are on the other. This allows the equation to be integrated directly, often resulting in a product of functions that can be separated and integrated individually.

💡Obvious Substitutions

Obvious substitutions refer to the process of identifying a part of the differential equation that can be simplified or transformed by introducing a new variable. This technique is particularly useful when the equation does not fit standard forms like homogeneous or linear equations. The term 'obvious' can be misleading, as it requires recognizing patterns or structures within the equation that suggest a potential substitution.

💡Homogeneous Equations

A homogeneous differential equation is one that can be written in a form where the equation is proportional to the solution. In the context of the video, the host discusses how the techniques used for obvious substitutions are similar to those used for homogeneous equations, particularly in the way substitutions are made and how the equation is transformed.

💡Chain Rule

The chain rule is a fundamental principle in calculus that is used to compute the derivative of a composite function. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In the context of the video, the chain rule is implicitly used when taking derivatives of the substitution variable 'V'.

💡Derivative

In calculus, the derivative of a function is a measure of the rate at which the function changes with respect to its independent variable. Derivatives are central to the study of differential equations, as they represent the instantaneous rate of change and are used to formulate and solve these equations.

💡Integration

Integration is the process of finding the function whose derivative is a given function, effectively the reverse operation of differentiation. In the context of the video, integration is used to solve differential equations after they have been transformed into a form that allows for integration, typically by separating variables or making obvious substitutions.

💡Trigonometric Substitution

Trigonometric substitution is a technique used to solve certain types of differential equations that involve square roots or other radicals. It involves expressing the equation in terms of trigonometric functions to simplify the integration process. The video mentions this as one of the methods that could potentially be used to solve a particular type of differential equation.

💡Implicit Solution

An implicit solution is a form of solution to a mathematical equation where the variables are not explicitly solved for individually but are expressed in terms of each other or in a combined form. In the context of the video, an implicit solution to a differential equation is one where the relationship between 'x' and 'y' is expressed in a combined form rather than solving for 'y' explicitly.

💡Bernoulli Equations

Bernoulli equations are a special class of differential equations that can be written in the form of a first-order linear differential equation with a variable coefficient. These equations are named after the Swiss mathematician Johann Bernoulli. The video script mentions Bernoulli equations as a topic for a future video, indicating that they are a type of differential equation that the host plans to cover.

Highlights

The video continues discussing techniques for solving differential equations, focusing on 'obvious substitutions'.

The term 'obvious' in 'obvious substitutions' may not always be intuitive, as it depends on recognizing patterns in the equations.

The goal with substitutions is to transform the equation into a form that is either separable or linear, allowing the use of previously learned techniques.

The concept of 'composition' is introduced as a key element to look for when identifying obvious substitutions in differential equations.

The technique is similar to solving homogeneous equations, where a substitution is made, and the equation is transformed to solve for y.

Derivatives play a crucial role in the substitution process, as they help replace variables and transform the equation.

The process involves identifying a composition, solving for y, taking a derivative, and then replacing all instances of y and dy/dx in the equation.

An example is provided to illustrate how to approach differential equations that do not fit the homogeneous model or other common forms.

The video emphasizes the importance of looking for compositions in the differential equation and solving for y within that composition.

The derivative of the substitution (dy/dx) is transformed into a form that can be integrated, which is crucial for solving the equation.

The process is demonstrated with a first-order differential equation, showing how to identify the composition and make the necessary substitutions.

The video shows how to manipulate the equation to create a separable form, which is essential for integration and solving the differential equation.

The concept of 'chain rule' is applied when taking derivatives with respect to x, which is implicit in the process of substitution.

The video provides a step-by-step walkthrough of solving a differential equation using the obvious substitution technique, emphasizing the importance of recognizing compositions.

The solution process involves integrating both sides of the equation after making the necessary substitutions and grouping variables appropriately.

The final solution is presented as an implicit solution to the differential equation, showing how the substitution technique can yield results even when explicit solutions are challenging.

The video concludes by reinforcing the similarities between the obvious substitution technique and solving homogeneous equations, emphasizing the adaptability of the approach.

Transcripts

Browse More Related Video

Substitutions for Homogeneous First Order Differential Equations (Differential Equations 20)

How Embedded Derivatives Can Make Differential Equations Easier (Differential Equations 25)

a very interesting differential equation

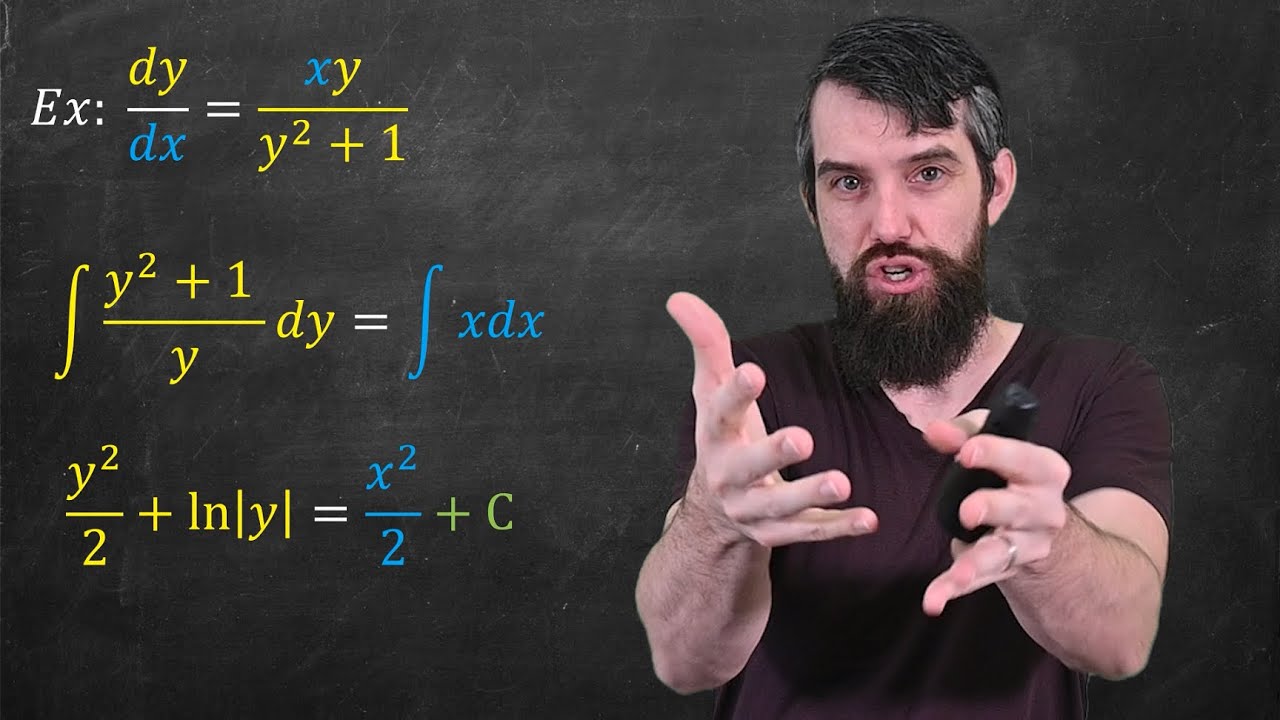
Separation of Variables // Differential Equations

Reducible Second Order Differential Equations, Missing Y (Differential Equations 26)

Homogeneous Differential Equations

Related Tags

Differential Equations Mathematics Tutorial Obvious Substitutions Advanced Math Educational Content Trigonometric Functions Integration Techniques Separable Equations Homogeneous Equations Math Video