Solving Homogeneous First Order Differential Equations (Differential Equations 21)

Professor Leonard

12 Nov 2018115:11

EducationalLearning

32 Likes 10 Comments

TLDRIn this instructional video, the presenter delves into solving homogeneous differential equations using substitution techniques. The video outlines the process of transforming given equations into a homogeneous form, where every instance of 'y' is expressed as 'y over x'. The presenter provides several examples, demonstrating how to identify the appropriate substitution and apply it to simplify the equation. The video emphasizes the importance of practice and understanding the underlying mathematical concepts to tackle more complex problems effectively.

Takeaways

📚 The video discusses techniques for solving homogeneous differential equations through substitution methods.
🔍 Identifying the appropriate substitution for a given differential equation is crucial for simplifying the problem and finding a solution.
📝 Practice is essential for mastering the techniques, as emphasized by the讲师 who provides numerous examples for the viewer to work through.
🤔 The讲师 highlights that some differential equations may have multiple solutions or can be approached with different techniques, so it's important to consider all possibilities.
🌟 The讲师 demonstrates the power of substitution in transforming complex equations into simpler, more manageable forms.
📊 The process of solving homogeneous equations often involves dividing terms, simplifying expressions, and applying integration techniques.
⚠️ The讲师 warns about potential domain restrictions when modifying differential equations, such as ensuring certain variables are not zero.
🧠 Understanding the underlying logic and mathematical principles behind each step is crucial for successfully applying these techniques.
🔑 The讲师 provides a key insight: when dealing with square roots in the equation, transforming the equation to avoid absolute values can simplify the process.
📈 The讲师 uses examples to illustrate how to handle complex fractions and how to revert back to the original variables after applying substitution.
🎯 The goal of the video is to equip viewers with the knowledge and practice needed to tackle difficult homogeneous differential equations with confidence.

Q & A

What is the main focus of the video script?
-The main focus of the video script is to teach the method of solving homogeneous differential equations using substitution techniques.
What is a homogeneous differential equation?
-A homogeneous differential equation is a type of differential equation where the terms can be rearranged to have every instance of the dependent variable (usually y) divided by the independent variable (usually x).
How does the substitution technique work in the context of homogeneous equations?
-The substitution technique involves dividing every term of the equation by a common factor, typically the independent variable (X), to structure the equation in a way that allows for separation of variables or other simplification techniques to be applied.
What is the first step in solving a homogeneous differential equation?
-The first step in solving a homogeneous differential equation is to rearrange the terms so that every instance of the dependent variable (Y) is divided by the independent variable (X), which often involves dividing all terms by X.
Why is it important to avoid absolute values in the solution process?
-Avoiding absolute values is important because they can complicate the solution process. In the context of limits and square roots, absolute values can introduce unnecessary complexity, and it's often preferable to work with expressions that are defined without the need for absolute values.
What is the role of domain restrictions in solving these equations?
-Domain restrictions are crucial because they define the valid range of values for the variables involved. When modifying a differential equation to fit a particular technique, it's necessary to ensure that the resulting expressions do not lead to undefined values, which would occur if denominators or terms that cannot be zero are set to zero.
How does the video script address the issue of domain restrictions?
-The video script addresses domain restrictions by pointing out that when certain operations are performed on the differential equation (like division), the expressions involved must not be zero to avoid undefined results. It emphasizes the need to be aware of these restrictions when applying techniques to solve the equations.
What is the significance of the substitution V = Y/X in homogeneous equations?
-The substitution V = Y/X is significant because it allows for the simplification of the equation by making every instance of Y a fraction over X. This substitution is a key step in transforming the equation into a form that can be solved using separation of variables or other techniques.
How does the video script handle complex fractions in the solution process?
-The video script handles complex fractions by multiplying both the numerator and the denominator by the least common denominator (LCD) to simplify the expression. This process is used to convert complex fractions into a form that can be more easily integrated or solved.
What is the final form of the solution for a homogeneous differential equation after applying the techniques discussed in the script?
-The final form of the solution for a homogeneous differential equation after applying the techniques discussed in the script is typically an implicit form involving the dependent variable (Y) and the independent variable (X), along with an arbitrary constant (C). The exact form depends on the specific equation and the techniques used to solve it.

Outlines

00:00

📚 Introduction to Homogeneous Equations

The paragraph introduces the concept of homogeneous equations and their solution techniques. It emphasizes the importance of practicing these techniques to internalize them. The speaker mentions that the video will cover several challenging examples, aiming to provide the most difficult cases to prepare the audience for various scenarios. The paragraph also hints at alternative methods to solve some of these equations, which will be explored in future videos.

05:07

🧠 Substitution Techniques for Homogeneous Equations

This paragraph delves into the process of solving homogeneous equations using substitution techniques. It explains the steps of structuring the equation, dividing by a common factor, and substituting variables to simplify the equation. The speaker guides through a specific example, highlighting the importance of grouping terms and handling derivatives during the substitution process. The paragraph emphasizes the goal of transforming the equation into a simpler, solvable form.

10:07

🔄 Solving with Substitution and Integrals

The paragraph discusses the continuation of solving homogeneous equations through substitution and integration. It outlines the process of simplifying the equation, performing integrations, and handling algebraic mistakes that may arise. The speaker provides a step-by-step walkthrough of the algebraic manipulations required to isolate variables and solve the differential equation. The paragraph also touches on the concept of negative exponents and their role in the substitution process.

15:19

📈 Integration and Solving for Y

This paragraph focuses on the integration process after setting up the homogeneous equation correctly. It explains how to integrate both sides of the equation and the importance of keeping track of constants and signs. The speaker demonstrates how to rearrange terms and combine logarithmic expressions to solve for the variable Y. The paragraph also addresses the potential complexity of the final answer and the importance of understanding the underlying algebraic steps.

20:22

🤔 Tackling More Complex Homogeneous Equations

The paragraph introduces more complex homogeneous equations and the approach to solving them. It emphasizes the importance of recognizing when a homogeneous substitution is apparent and the potential for multiple solutions. The speaker provides an example of dividing by x squared to simplify the equation and the necessity of handling square roots carefully. The paragraph also discusses the potential for different forms of the final solution and the importance of understanding the implications of each form.

25:24

🌟 Advanced Techniques and Partial Fractions

This paragraph discusses the use of advanced techniques such as partial fractions in solving certain types of homogeneous equations. The speaker introduces the concept of embedded derivatives and the possibility of using different techniques for the same equation. The paragraph also warns about the potential for more challenging problems and encourages the audience to try simple techniques first before resorting to more complex methods. The speaker assures that even if a problem appears difficult, there's a good chance a substitution will work.

30:25

🧩 Putting the Pieces Together

The paragraph focuses on the final steps of solving a homogeneous equation, including the use of substitution and integrals. It describes the process of simplifying complex fractions, moving terms around, and combining logarithms to reach a solvable form. The speaker also emphasizes the importance of understanding the algebraic manipulations involved and the various forms that the final solution can take. The paragraph concludes with the speaker expressing satisfaction with the complexity of the problem and the audience's ability to handle it.

Mindmap

Keywords

💡Homogeneous Differential Equations

Homogeneous differential equations are a type of differential equation where the dependent variable and its derivatives appear in the same ratio. In the context of the video, the speaker is discussing how to solve these equations using substitution techniques, specifically by making the equation homogeneous and then applying methods suitable for the resulting form.

💡Substitution Technique

The substitution technique is a method used in calculus to simplify complex equations. In the video, the speaker uses this technique to transform differential equations into a form that can be more easily solved. The process involves replacing a variable or a function of a variable with another variable, which is then used to solve the equation.

💡Separation of Variables

Separation of variables is a technique used to solve first-order differential equations by rearranging the equation so that all terms with the variable are on one side and all terms with the derivative are on the other side. This allows for the equations to be integrated directly. In the video, the speaker discusses using this method after making the differential equation homogeneous.

💡Integration

Integration is a fundamental process in calculus that involves finding the antiderivative of a function, which gives the function whose derivative is the original function. In the context of the video, the speaker uses integration to solve differential equations after transforming them into a solvable form.

💡Derivative

A derivative is a mathematical concept that represents the rate of change of a function with respect to its independent variable. In the video, the speaker discusses how to handle derivatives when solving differential equations, particularly through the use of substitution and separation of variables.

💡Antiderivative

An antiderivative, also known as an indefinite integral, is a function whose derivative is equal to the given function. In the context of the video, finding the antiderivative is a crucial step in solving differential equations through integration.

💡Product Rule

The product rule is a fundamental calculus rule that allows for the differentiation of a product of two functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the video, the product rule is implicitly used when differentiating the substitution V = y/X.

💡Chain Rule

The chain rule is a calculus rule that is used to find the derivative of a composite function. It states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. In the video, the chain rule is used when differentiating the substitution V = y/X to find dy/dx.

💡Domain Restrictions

Domain restrictions refer to the set of allowable input values for a function, within which the function is defined and behaves as expected. In the context of the video, the speaker discusses how certain techniques for solving differential equations can impose restrictions on the domain of the original problem.

💡Absolute Value

The absolute value of a number is its non-negative value, without regard to its sign. In the video, the speaker discusses how to handle absolute values when solving differential equations, particularly in the context of square roots and separation of variables.

Highlights

The video discusses the technique of solving homogeneous differential equations through substitution.

The讲师 emphasizes在解决这类方程时，要确保每个Y都除以X，即Y/X的形式。

介绍了如何通过将每个Y替换为V，并将dy/dx替换为x*dV/dx + B，来进行变量替换。

讲师提到，有时候这些方程可以通过其他方法解决，但本视频专注于介绍一种通用的解决方法。

讲师展示了如何通过简化和重新排列项来将方程转化为更易于处理的形式。

在解决一个具体的方程时，讲师详细解释了如何通过分组和找到共同的分母来简化方程。

讲师强调了在处理分数时要小心，避免在找到共同分母时犯常见的代数错误。

讲师提到，有时候方程看起来很难，但通过合适的变量替换，可以变得更简单。

讲师展示了如何通过将方程的右边部分转化为关于V的函数，来简化问题。

讲师解释了如何通过对数和指数函数的使用，将复杂的方程转化为更简单的形式。

讲师强调了在解决这些方程时，要尝试不同的方法，不要立即跳到最复杂的解决方案。

讲师提到，尽管有些方程可能看起来很难，但通过练习和应用适当的技术，可以找到解决方案。

讲师展示了如何通过变量替换和分离变量来解决看似复杂的方程。

讲师强调了在解决方程时，要注意定义域的限制，确保在操作过程中不会得到未定义的表达式。

讲师提到，尽管有些方程可能需要使用部分分式法等高级技术，但首先应该尝试更简单的方法。

讲师总结了如何通过一系列代数操作和变量替换，将非齐次方程转化为齐次方程的形式。

Transcripts

Browse More Related Video

Substitutions for Homogeneous First Order Differential Equations (Differential Equations 20)

Solving Differential Equations with a Composition (Obvious) Substitution (Differential Equations 22)

First order, Ordinary Differential Equations.

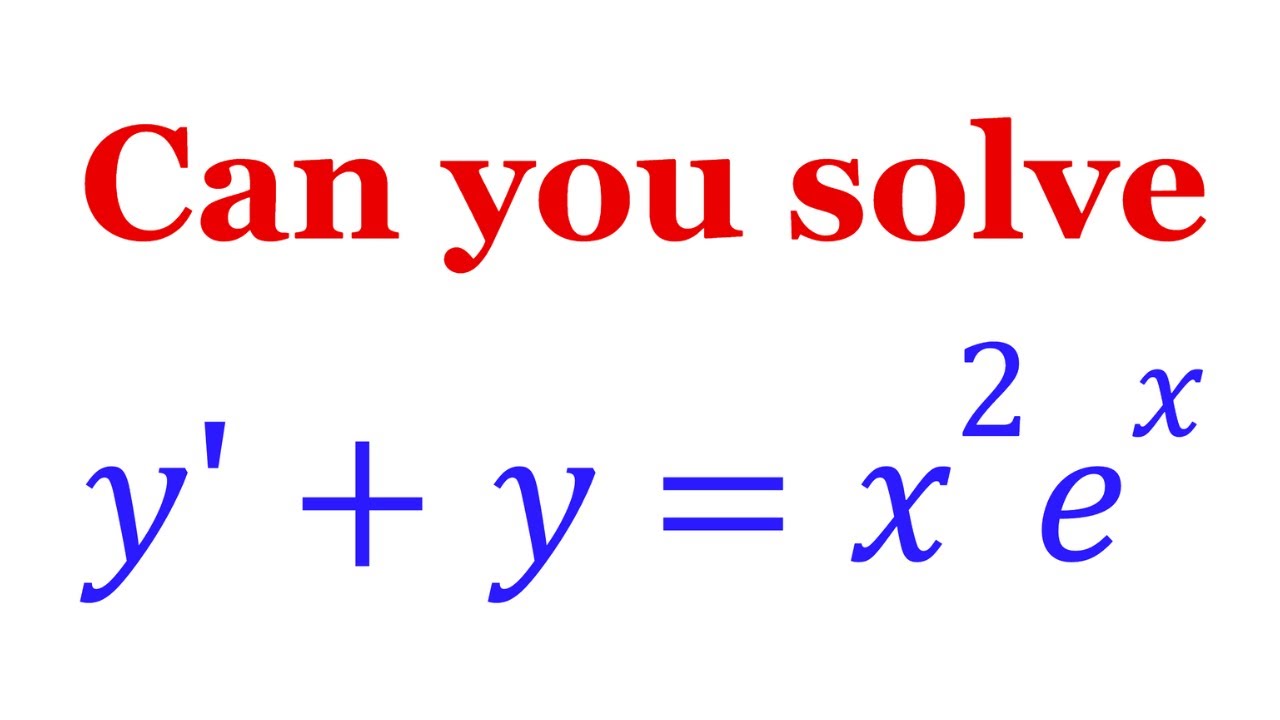
Let's Solve An Interesting Differential Equation

Reducible Second Order Differential Equations, Missing X (Differential Equations 27)

How Embedded Derivatives Can Make Differential Equations Easier (Differential Equations 25)

Related Tags

Differential Equations Homogeneous Equations Substitution Methods Domain Restrictions Algebraic Techniques Integration Strategies Mathematical Analysis Educational Content Complex Fractions Absolute Value