High School Physics - Frequency and Period

Dan Fullerton
12 Apr 201507:56
EducationalLearning
32 Likes 10 Comments

TLDRIn this lesson, Dan Fullerton explains the concepts of frequency and period, their importance in physics, and how they are related. He uses the examples of a toy train and a person on a roundabout to demonstrate calculations for centripetal acceleration, force, period, and frequency. The lesson emphasizes the practical application of these concepts in understanding motion in circular paths and prepares students for further study of waves.

Takeaways
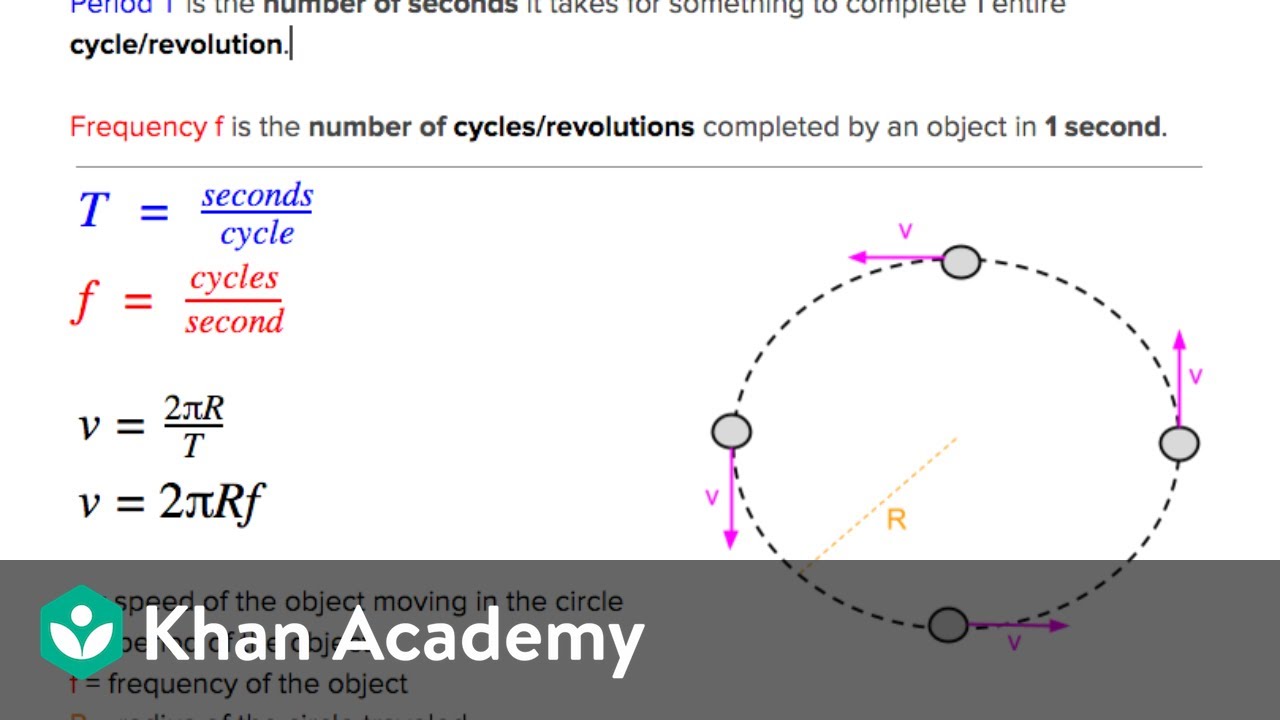
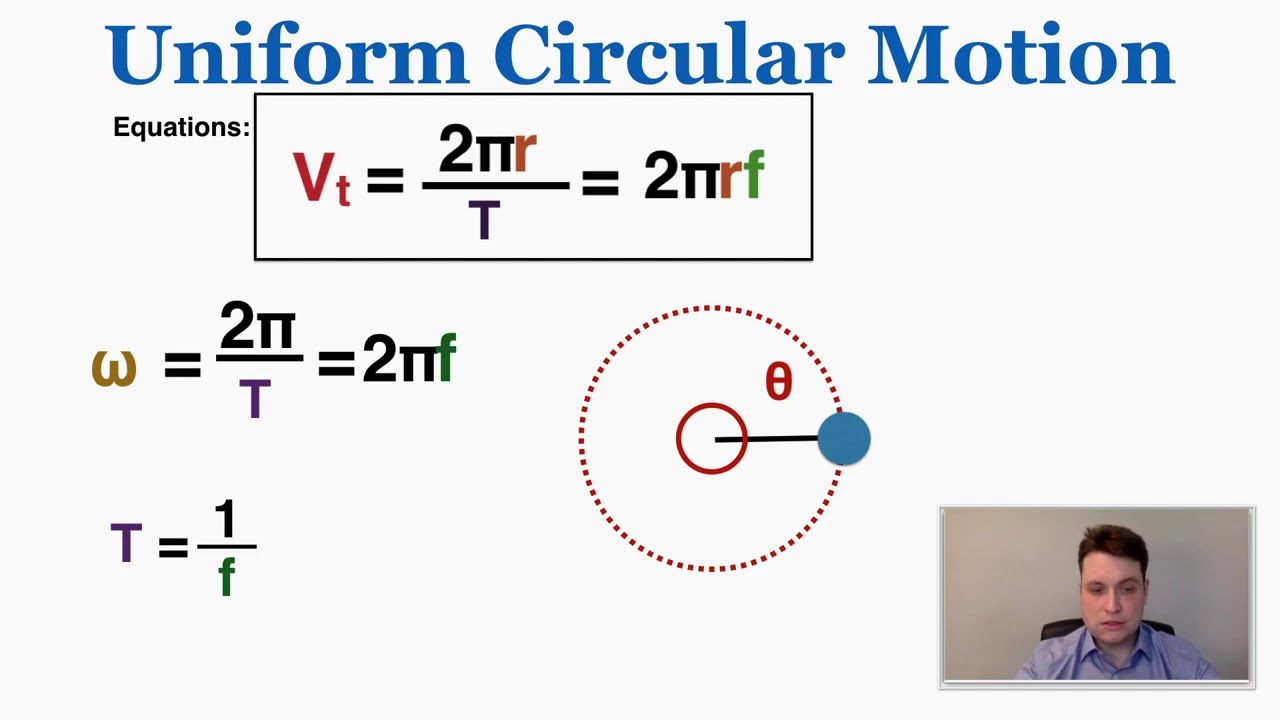
  • 📊 Frequency (F) is the number of revolutions or cycles per second and is symbolized by 'F' with units in Hertz (Hz).
  • 🔄 Period (T) is the time taken for one complete revolution or cycle, symbolized by 'T' with units in seconds.
  • 🔗 The relationship between frequency and period is inversely proportional, where T is the reciprocal of F (T = 1/F) and vice versa.
  • 🚂 In the toy train example, the train completes 10 laps on a circular track in 100 seconds with a track diameter of 1 meter, leading to a radius of 0.5 meters.
  • 📐 Centripetal acceleration is calculated using the formula 'v^2 / R', where 'v' is the linear speed and 'R' is the radius of the circular path.
  • 💥 Centripetal force is determined by multiplying the mass of the object by its centripetal acceleration (Fc = m * ac).
  • 🏃‍♂️ Allan's example involves making 38 complete revolutions on a playground roundabout in 30 seconds with a radius of 1 meter.
  • 🕒 From Allan's revolutions, the period is calculated as 30/38 seconds and the frequency is the inverse, approximately 1.27 Hz.
  • 🏃‍♂️ Speed calculation for Allan is based on the distance covered (38 circumferences) divided by the time taken (30 seconds), resulting in a speed of 7.96 m/s.
  • 🔍 The centripetal force experienced by Allan is calculated using his mass (40 kg), the square of his speed (7.96 m/s), and the radius of the roundabout (1 m), yielding approximately 2,503 Newtons.
  • 📘 The lesson emphasizes the importance of understanding frequency and period as they are fundamental concepts in physics, especially in the study of waves.
Q & A

  • What is the definition of frequency?

    -Frequency, symbolized as 'F', is the number of revolutions or cycles that occur each second. It can also be thought of as the number of activities or events that occur per second.

  • What are the units for frequency?

    -The units for frequency are 1/seconds per second, which is also known as Hertz, abbreviated as 'Hz'.

  • How is the frequency related to the period?

    -Frequency and period are closely related. The period is the time it takes for one complete revolution or cycle, and its units are seconds. The period is calculated as 1 divided by the frequency, and likewise, the frequency is 1 divided by the period.

  • What is the formula for centripetal acceleration?

    -The formula for centripetal acceleration is v^2 / R, where 'v' is the speed of the object and 'R' is the radius of the circular path it is moving in.

  • How do you calculate the centripetal force?

    -Centripetal force is calculated by multiplying the mass of the object (in kilograms) by its centripetal acceleration.

  • What is the relationship between the speed of an object and the circumference of the path it is moving on?

    -The speed of an object is calculated as the distance traveled (circumference of the path) divided by the time taken to travel that distance.

  • How long does it take for the 500g toy train to complete one lap of its circular track?

    -The 500g toy train takes 10 seconds to complete one lap of its circular track, as it completes 10 laps in 100 seconds.

  • What is the centripetal acceleration of the toy train?

    -The centripetal acceleration of the toy train is approximately 0.197 m/s^2, calculated using the formula v^2 / R with a speed of 0.314 m/s and a radius of 0.5 meters.

  • What is the centripetal force acting on the 500g toy train?

    -The centripetal force acting on the 500g toy train is approximately 0.099 Newtons, calculated by multiplying the mass in kilograms (0.5 kg) by the centripetal acceleration (0.197 m/s^2).

  • How many revolutions does Allan make on the playground roundabout in 30 seconds?

    -Allan makes 38 complete revolutions on the playground roundabout in 30 seconds.

  • What is Allan's centripetal force?

    -Allan's centripetal force is approximately 2,530 Newtons, calculated using his mass (40 kg), his speed (7.96 m/s), and the radius of the roundabout (1 meter) with the formula mv^2/R.

Outlines
00:00
📘 Introduction to Frequency and Period

This paragraph introduces the concepts of frequency (F) and period (T) as fundamental physical quantities, particularly important in the study of waves. Frequency is defined as the number of revolutions or cycles per second, symbolized by 'F', and measured in Hertz (Hz). The period is the time taken for one complete revolution or cycle, symbolized by 'T', and measured in seconds. The relationship between frequency and period is highlighted, where period is the reciprocal of frequency and vice versa. The paragraph begins with an example of calculating frequency and period for an object moving in a circle at constant speed, setting the stage for solving more complex problems later in the lesson.

05:04
🔧 Sample Problem: Toy Train on a Circular Track

The paragraph presents a sample problem involving a toy train completing laps on a circular track. The problem requires calculating the train's centripetal acceleration, centripetal force, period, and frequency. Given the train completes 10 laps in 100 seconds on a track with a one-meter diameter, the radius is determined to be 0.5 meters. Using the formula for centripetal acceleration (v^2 / R), the speed is calculated based on the distance covered (10 times the circumference) divided by time. With the speed calculated, the centripetal acceleration and force are then determined using the respective formulas. The period is calculated as the time for one lap, and the frequency is found as the inverse of the period.

🎢 Sample Problem: Allan on the Playground Roundabout

This paragraph discusses another sample problem, where Allan makes 38 complete revolutions on a playground roundabout in 30 seconds with a radius of 1 meter. The period is calculated as the time for one revolution, and the frequency is the inverse of the period. The speed at which Allan revolves is determined using the formula for speed (distance over time), considering the number of revolutions and the radius of the roundabout. Finally, the centripetal force on Allan is calculated using his mass and the previously determined speed and radius, applying the formula for centripetal force (mass times centripetal acceleration). The problem illustrates the application of the concepts of frequency, period, speed, and centripetal force in a real-world scenario.

Mindmap
Keywords
💡Frequency
Frequency, symbolized as 'F', refers to the number of revolutions or cycles that occur each second. It is a measure of how often a repeating event happens within a given timeframe. In the context of the video, frequency is used to describe the rate at which an object, such as a toy train or a person on a roundabout, completes a full cycle of motion. The unit for frequency is Hertz (Hz), which is equivalent to 1 cycle per second. For instance, if the toy train completes 10 laps in 100 seconds, its frequency is 0.1 Hz, calculated as 1/(100 seconds).
💡Period
The period is the time it takes for one complete revolution or cycle of an event. It is the inverse relationship of frequency, where the period is equal to 1 divided by the frequency. The unit for period is seconds. In the video, the period is used to describe the duration of time an object takes to complete one full cycle. For example, if an object takes 10 seconds to complete one cycle, its period is 10 seconds.
💡Centripetal Acceleration
Centripetal acceleration is the acceleration experienced by an object moving in a circular path. It is directed towards the center of the circle and is responsible for keeping the object in circular motion. The formula for centripetal acceleration is given by 'a = v^2 / R', where 'a' is the acceleration, 'v' is the velocity of the object, and 'R' is the radius of the circular path. In the video, centripetal acceleration is used to calculate the force required to keep the toy train moving in a circular track and the force acting on a person revolving on a roundabout.
💡Centripetal Force
Centripetal force is the force that keeps an object moving in a circular path. It is always directed towards the center of the circle and is necessary to change the direction of the object's velocity without changing its speed. The formula for centripetal force is 'F = m * a_c', where 'F' is the force, 'm' is the mass of the object, and 'a_c' is the centripetal acceleration. In the video, centripetal force is used to determine the force acting on the toy train and on a person revolving on a roundabout.
💡Speed
Speed is a measure of how fast an object is moving, defined as the distance traveled per unit of time. It is a scalar quantity and does not involve direction. In the context of the video, speed is used to describe the rate at which an object covers distance in a circular path. The formula for speed is 'v = d / t', where 'v' is the speed, 'd' is the distance, and 't' is the time taken.
💡Circumference
Circumference is the total distance around the edge of a circular path or object. It is a linear measure that corresponds to the perimeter of a circle. The formula for the circumference of a circle is 'C = 2 * pi * R', where 'C' is the circumference, 'pi' is a mathematical constant approximately equal to 3.14159, and 'R' is the radius of the circle. In the video, circumference is used to calculate the distance covered by an object in a circular motion.
💡Radius
The radius of a circle is the distance from the center of the circle to any point on its edge. It is a linear measure and a fundamental property of a circle. In the context of the video, the radius is used to describe the size of the circular path and to calculate other quantities such as speed, period, and centripetal acceleration.
💡Revolution
A revolution is a complete turn or cycle around a central point or axis. In the context of the video, revolution is used to describe the motion of an object moving in a circular path, such as a toy train around a track or a person on a playground roundabout. The number of revolutions per unit of time is a measure of frequency.
💡Hertz
Hertz (Hz) is the unit of measurement for frequency. It is defined as one cycle per second. The term 'Hertz' is used in the video to express the frequency of an object's motion in a circular path, such as the toy train and the person on the roundabout.
💡Newtons
Newtons is the unit of measurement for force in the International System of Units (SI). It is defined as the force required to accelerate a one-kilogram mass by one meter per second squared. In the video, Newtons is used to express the magnitude of the centripetal force acting on objects moving in a circular path, such as the toy train and the person on the roundabout.
💡Physics
Physics is the natural science that studies matter, its motion, and the related energy and forces. In the video, physics principles are applied to analyze the motion of objects in circular paths, including concepts such as frequency, period, centripetal acceleration, and force. The video aims to provide a foundational understanding of these concepts, which are essential in the study of waves and other physical phenomena.
Highlights

The lesson focuses on understanding frequency and period, key concepts in physics.

Frequency (F) is the number of revolutions or cycles per second, symbolized by the unit Hertz (Hz).

Period (T) is the time taken for one complete revolution or cycle, measured in seconds.

Frequency and period are inversely related; period is the reciprocal of frequency and vice versa.

A 500g toy train example is used to demonstrate the calculation of centripetal acceleration, force, period, and frequency.

Centripetal acceleration is calculated using the formula v^2 / R, where v is the linear speed and R is the radius of the circular path.

The speed of the toy train is determined by dividing the total distance traveled by the time taken.

Centripetal force is calculated by multiplying the mass of the object by its centripetal acceleration.

The period of the toy train is calculated by dividing the total time by the number of laps completed.

Frequency is calculated as the inverse of the period, providing the number of cycles per second.

A second example involves Allan making 38 complete revolutions on a playground roundabout in 30 seconds.

Allan's period is calculated by dividing the time by the number of revolutions.

Frequency is found by taking the reciprocal of the period.

Allan's speed is determined by calculating the distance traveled per unit of time.

Centripetal force on Allan is calculated using his mass, speed, and the radius of the roundabout.

The lesson emphasizes the importance of understanding frequency and period for future topics in physics, such as waves.

For further assistance or information, the website A+ Physics is recommended.

The practical application of these concepts is demonstrated through sample problems, making the lesson engaging and informative.

Transcripts

Browse More Related Video

AP Physics 1 review of Centripetal Forces | Physics | Khan Academy

Uniform Circular Motion - IB Physics

Uniform Circular Motion Formulas and Equations - College Physics

AP Physics 1: Rotational Kinematics Review

Transverse Waves Grade 10

High School Physics - Wave Characteristics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsLessonFrequencyCalculationPeriodConceptsCircularMotionWaveUnitDanFullertonCentripetalAccelerationCentripetalForcePhysicsEducationMathematicalAnalysis