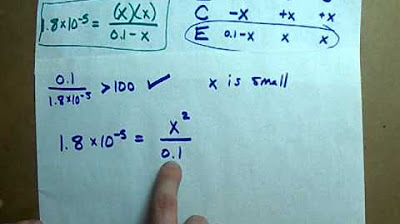Calculating pH for a Weak Acid Solution (Using ICE Chart)
TLDRThe video script provides a detailed tutorial on calculating the pH of a weak acid solution, emphasizing the importance of understanding the equilibrium concentration of H+ ions. It clarifies that the initial concentration of the weak acid is much greater than the H+ concentration produced and introduces the concept of the Ka value. The script walks through the process using an example of a one M solution of hydrofluoric acid (HF), explaining the use of an ICE (Initial, Change, Equilibrium) chart to determine the equilibrium concentrations and the application of the 5% rule to verify assumptions. The final calculation yields a pH value of 1.57, highlighting the significance of precision and the proper use of scientific methods in such calculations.
Takeaways
- 📚 The video explains how to calculate the pH for a weak acid solution, emphasizing that the initial concentration of the weak acid is much greater than the concentration of H+ produced.
- 🔍 The pH is calculated using the formula pH = -log[H+], where [H+] represents the concentration of hydrogen ions in the solution.
- 🧪 For weak acids, one cannot directly use the initial concentration of the acid as the concentration of H+; instead, the equilibrium concentration of H+ must be determined.
- 📊 An ICE (Initial, Change, Equilibrium) chart is used to set up the reaction and track the concentrations of reactants and products at equilibrium.
- 🌟 HF is identified as a weak acid because it is not on the list of strong acids and has a Ka value less than one.
- 🔄 The direction of the reaction is determined by the initial conditions, with the assumption that the reaction will move forward to establish equilibrium.
- 📐 The Ka expression is used to solve for the change in concentration (x) at equilibrium, considering the coefficients in the balanced chemical equation.
- 🤔 An assumption is made that the initial concentration of the weak acid remains essentially unchanged due to the small Ka value, simplifying the calculation.
- 📈 The 5% rule is applied to verify the assumption, ensuring that the change in concentration (x) is less than 5% of the initial concentration.
- 🎯 The final step is to calculate the pH using the negative log of the equilibrium H+ concentration, yielding the pH value for the weak acid solution.
Q & A
What is the main topic of the video?
-The main topic of the video is how to calculate the pH for a weak acid solution.
Why can't we use the initial concentration of the weak acid as the concentration of H+ in the calculation?
-The initial concentration of the weak acid is much greater than the concentration of H+ produced. Since weak acids do not fully dissociate, the concentration of H+ will be significantly less than the initial concentration of the weak acid.
What is the formula to calculate pH?
-The formula to calculate pH is pH = -log[H+], where [H+] represents the concentration of hydrogen ions in the solution.
Why is it important to determine the equilibrium concentration for H+ when calculating pH for a weak acid solution?
-It is important because weak acids do not fully dissociate, and the concentration of H+ at equilibrium is different from the initial concentration of the weak acid. Determining the equilibrium concentration for H+ allows for an accurate calculation of pH.
What is an ICE chart and how is it used in this context?
-An ICE chart stands for Initial, Change, and Equilibrium. It is used to keep track of the concentrations of reactants and products at different stages of the reaction, which helps in determining the equilibrium concentration of H+ for calculating pH.
What is the role of the Ka value in the calculation of pH for a weak acid solution?
-The Ka value represents the equilibrium constant for the dissociation of the weak acid. It is used in the calculation to find the equilibrium concentrations of the species involved in the reaction, which in turn allows us to determine the concentration of H+ and thus the pH.
How can we verify if our assumption in the calculation is valid?
-We can use the 5% rule to verify our assumption. The rule states that if the change in concentration (x) is less than 5% of the initial concentration, the assumption is valid. This ensures that the approximation we made by neglecting the change in concentration is acceptable.
What is the significance of the 5% rule in the calculation?
-The 5% rule is a check to ensure that the assumption made in simplifying the Ka expression (ignoring the change in concentration) is reasonable. If the change in concentration (x) is less than 5% of the initial concentration, it confirms that the approximation does not significantly affect the result and the calculation is valid.
What was the Ka value given in the example?
-The Ka value given in the example was 7.2 * 10^-4.
How was the equilibrium concentration of H+ ([H+]) calculated in the example?
-In the example, the equilibrium concentration of H+ ([H+]) was calculated by setting up the Ka expression with the equilibrium concentrations of HF, H3O+, and F-, and solving for x. The assumption was made that the initial concentration of HF (1 M) would remain essentially unchanged due to the small Ka value. The 5% rule was then applied to verify this assumption, and the square root of Ka was taken to find the [H+].
What was the calculated pH for the 1 M HF solution in the example?
-The calculated pH for the 1 M HF solution was found to be 1.57 after determining the equilibrium concentration of H+ and applying the pH formula.
How many significant figures should the calculated pH value have?
-The calculated pH value should have the same number of significant figures as the concentration of H+ used in the calculation. In the example, both the [H+] concentration and the pH value have two significant figures.
Outlines
📚 Introduction to Calculating pH for Weak Acid Solutions
This paragraph introduces the concept of calculating the pH for a weak acid solution. It emphasizes the importance of understanding that the initial concentration of the weak acid is much greater than the concentration of H+ ions produced. The video explains that the concentration of the acid given cannot be used directly as the H+ concentration in the calculation. Instead, the equilibrium concentration of H+ must be determined. The paragraph also introduces the pH calculation formula, which is the negative log of H+ concentration. The example given is to calculate the pH for a one M solution of hydrochloric acid, highlighting that HF is a weak acid, and an ICE (Initial, Change, Equilibrium) chart is needed to find the equilibrium concentrations.
🧪 Using the ICE Chart and 5% Rule for Weak Acid Calculation
This paragraph delves into the process of using an ICE chart to calculate the pH of a weak acid solution. It explains how to set up the chart by writing the reaction between the weak acid and water, and how to determine the initial, change, and equilibrium concentrations. The paragraph discusses the direction of the reaction and how to make an educated assumption about the change in concentration based on the Ka value. It introduces the 5% rule as a verification method to ensure the assumption's accuracy, explaining that the x value (change in concentration) should be less than 5% of the initial value. The summary also covers how to solve for x using the Ka expression and how to calculate the final concentration of H+ at equilibrium. The paragraph concludes with the application of the pH formula using the calculated H+ concentration, resulting in a pH value of 1.57, and emphasizes the importance of significant figures in the calculation.
Mindmap
Keywords
💡pH calculation
💡Weak acid
💡Equilibrium concentration
💡H+ concentration
💡Ka value
💡ICE chart
💡Equilibrium
💡Negative log
💡5% rule
💡Significant figures
Highlights
The video explains how to calculate the pH for a weak acid solution.
The concentration of the weak acid initially put into the solution is much greater than the concentration of H+ produced.
The concentration of the acid given cannot be used as the value of H+ in calculations.
The equilibrium concentration for H+ must be determined to calculate pH.
The pH is calculated using the equation pH = -log[H+].
An example calculation is given for a one M solution of hydrochloric acid.
HF is recognized as a weak acid, not on the strong acid list and with a Ka less than one.
An ICE (Initial, Change, Equilibrium) chart is used to determine the concentration changes at equilibrium.
The reaction for HF in water is written as HF + H2O ⇌ H3O+ + F-.
The initial concentration of HF is 1.0 mol and concentrations of H3O+ and F- start at zero.
The direction of the reaction is determined to be forward, reducing HF and increasing H3O+ and F- concentrations.
The Ka expression and value are used to solve for the equilibrium concentration of H+.
An assumption is made that the initial concentration of HF is approximately equal to one minus the amount used up, due to the small Ka value.
The 5% rule is introduced to verify the assumption, checking if the x value is less than 5% of the initial value.
The calculated concentration of H+ at equilibrium is 2.7 * 10^-2 M.
The pH is found to be 1.57 using the calculated H+ concentration.
The importance of using significant figures is emphasized, with pH and H+ concentration both having two significant figures.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: