Work, Energy and Power in CrossFit Solutions, Part 2

Dan Fullerton
29 Dec 201313:08
EducationalLearning
32 Likes 10 Comments

TLDRIn this informative video, the presenter, Dan Fullerton, delves into the concepts of work, energy, and power within the context of CrossFit exercises. He illustrates these principles through various scenarios featuring athletes like Tom, Chris, Heidi, James, and Aaron, who perform different workouts such as thrusters, toes to bar, rope climbs, pull-ups, and box jumps. By calculating the force, displacement, and time, the video demonstrates how to determine the work done and power generated during these activities, as well as the energy expenditure and potential velocities involved. The video concludes with a reminder that despite the energy exerted, the net work is zero due to the return to the starting position, reinforcing the understanding of physical principles in the realm of fitness.

Takeaways
  • 🏋️‍♂️ In the CrossFit problem set, Tom performs 10 thrusters with a 45 kg barbell in 20 seconds.
  • 🔢 The applied force to lift the barbell is at least equal to its weight (45 kg * 9.8 m/s²), resulting in 441 Newtons.
  • 🚀 The work done in lifting the barbell for 2 seconds is calculated as force * displacement, equaling 662 Joules.
  • 💪 The power developed in lifting the bar is the work done per unit of time, calculated as 331 Watts.
  • 📈 For the entire 20 seconds, the net work performed on the bar is zero since the total displacement is zero.
  • 🏃‍♀️ Chris does toes to Bar with a period of 1.4 seconds per repetition and a frequency of 0.71 Hertz.
  • 🧗 Heidi climbs a rope with a minimum force equal to her weight (50 kg * 9.8 m/s²), which is 490 Newtons.
  • 🌐 The minimum work and energy Heidi must expend to climb the rope is 2,450 Joules.
  • 🔄 If Heidi releases the rope at the top, her potential energy is converted into kinetic energy, with a final velocity of approximately 9.9 m/s.
  • 🤸‍♂️ James executes butterfly chest to Bar pull-ups with a frequency of 0.875 Hertz and a period of 1.14 seconds per pull-up.
  • 🏆 Aaron jumps onto a 0.6 m box, doing 20 jumps in 52 seconds, with each jump requiring 300 Joules of work and energy.
Q & A

  • What is the mass of the barbell Tom uses for thrusters?

    -The mass of the barbell Tom uses is 45 kg.

  • How much force does Tom need to apply to lift the barbell upwards?

    -Tom needs to apply a force equal to at least the weight of the barbell, which is 441 Newtons (45 kg times 9.8 m/s^2).

  • What is the total work done by Tom while lifting the barbell for 2 seconds?

    -The total work done by Tom is 662 Joules (Force of 441 Newtons times displacement of 1.5 meters).

  • What is the power developed by Tom while lifting the barbell?

    -The power developed is 331 Watts (Work done of 662 Joules divided by time of 2 seconds).

  • What is the period of each toes to bar exercise performed by Chris?

    -The period of each toes to bar exercise is 1.4 seconds (28 seconds for 20 repetitions).

  • What is the minimum force Heidi must apply to the rope to move upward?

    -Heidi must apply a force equal to her weight, which is 490 Newtons (50 kg times 9.8 m/s^2).

  • How much work does Heidi do to climb the rope?

    -Heidi does 2450 Joules of work (Force of 490 Newtons times displacement of 5 meters).

  • What is Heidi's gravitational potential energy at the top of the rope?

    -Heidi's gravitational potential energy at the top is 2450 Joules (same as the work done to climb the rope).

  • What would be Heidi's velocity if she were to release the rope at the highest point?

    -Heidi's velocity would be approximately 9.9 m/s (square root of 2 times 9.8 m/s^2 times 5 m, neglecting air resistance).

  • How many seconds does it take for Aaron to complete each box jump?

    -It takes Aaron approximately 2.6 seconds to complete each box jump (52 seconds for 20 jumps).

  • What is the total energy expended by Aaron for the 20 box jumps?

    -The total energy expended by Aaron is 6000 Joules (300 Joules per jump multiplied by 20 jumps).

  • What is the average power expended by Aaron during the 20 box jumps?

    -The average power expended by Aaron is 115 Watts (6000 Joules divided by 52 seconds).

Outlines
00:00
🏋️‍♂️ Work, Energy, and Power in CrossFit: Tom's Thrusters

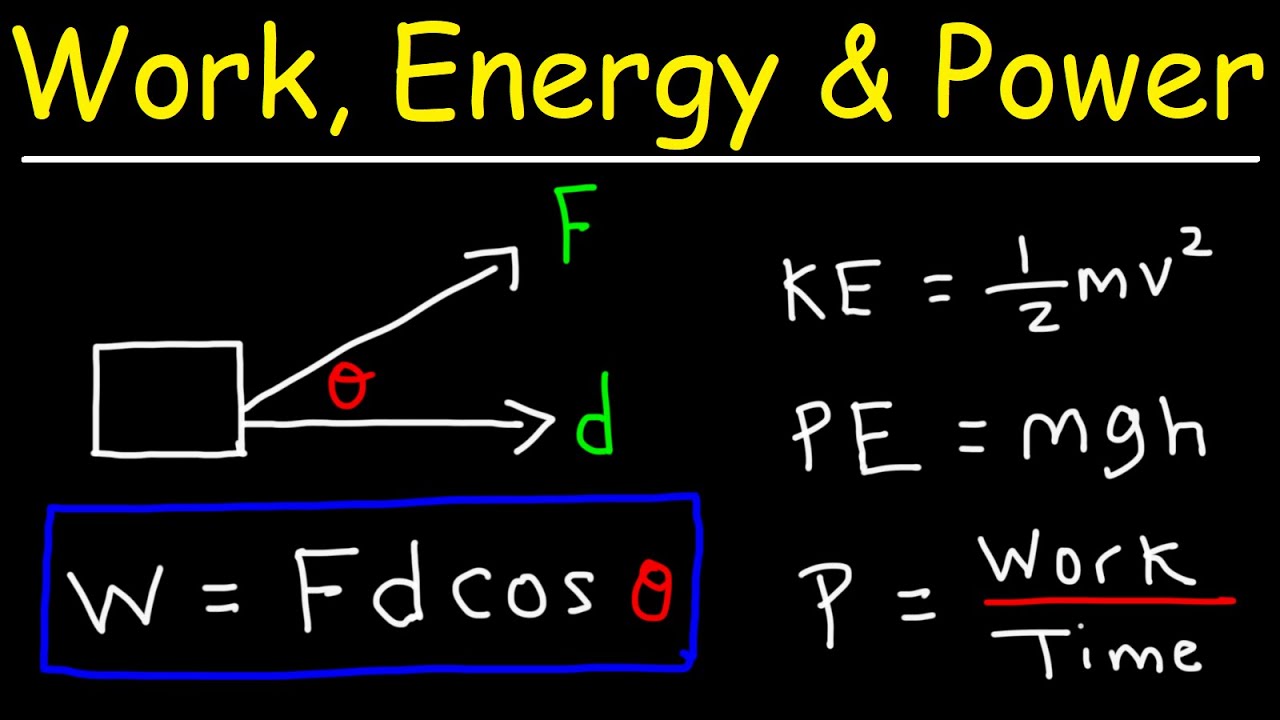
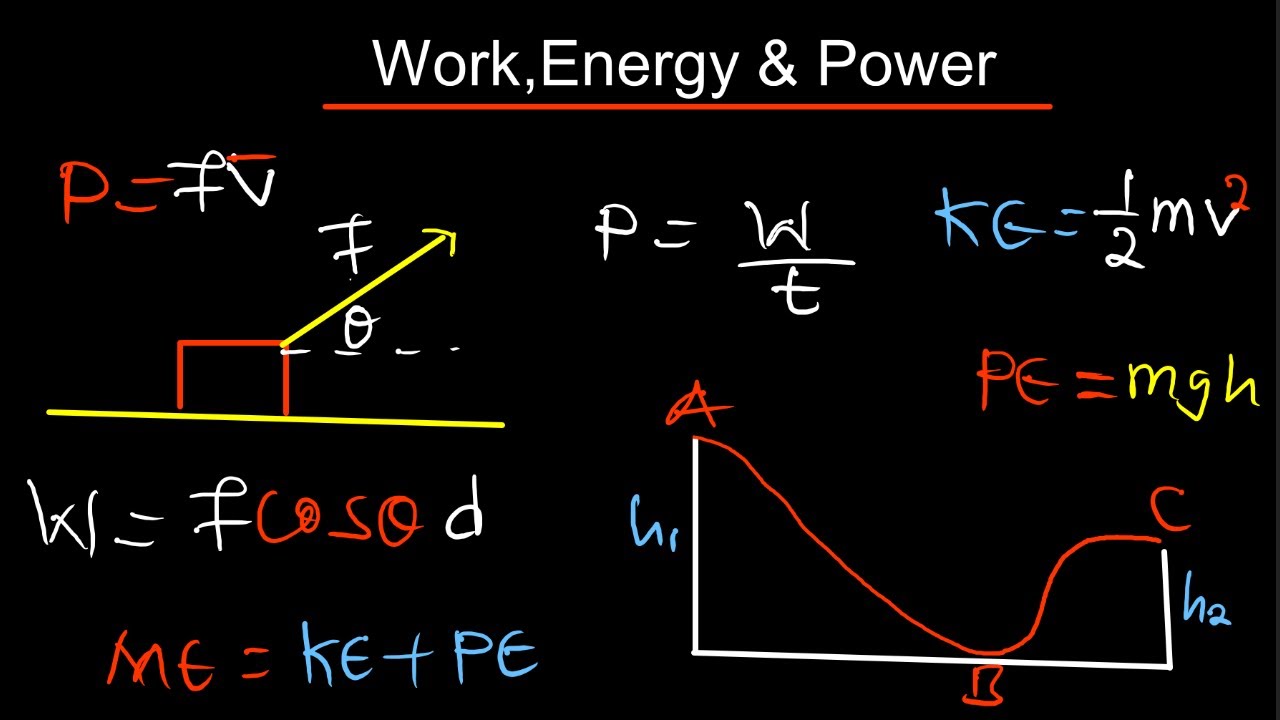
This paragraph introduces the video's focus on solving work, energy, and power problems related to CrossFit exercises, starting with Tom's performance of thrusters. Tom uses a 45 kg barbell and completes the exercise in 20 seconds. The analysis begins with a free body diagram, identifying the applied force (f_app) and the weight of the barbell. The required force to lift the barbell is equal to its mass (45 kg) times the acceleration due to gravity (9.8 m/s^2), totaling 441 Newtons. The work done (W) in lifting the barbell from 7 m to 2.2 m in 2 seconds is calculated as force (F) times displacement (s), resulting in 662 Joules. Power (P), the rate of doing work, is then determined by dividing the work by the time, yielding 331 Watts. The paragraph concludes by discussing the net work done on the barbell over the entire 20 seconds, which is zero since the barbell returns to its starting position.

05:02
🤸‍♀️ CrossFit Analysis: Chris's Toes to Bar and Heidi's Rope Climb

The second paragraph delves into Chris's toes to Bar exercise and Heidi's rope climb, analyzing their periods, frequencies, and the forces involved. Chris performs 20 repetitions in 28 seconds, leading to a period of 1.4 seconds per repetition and a frequency of 0.71 Hz. Heidi, with a mass of 50 kg, climbs 5 m three times in 40 seconds. The minimum force she must apply to the rope is her weight in Newtons (490 N). The work done by Heidi is 2,450 Joules, which is also the minimum energy she expends. Her gravitational potential energy at the top of the rope is calculated as 2,450 Joules, which, if she were to release the rope, would convert into kinetic energy. Using the conservation of energy principle, her velocity upon release would be approximately 9.9 m/s. The paragraph also calculates Heidi's maximum kinetic energy if she were to jump from the top of the rope, which equals the potential energy at the top.

10:10
🏃‍♂️ Energy Expenditure and Power Output: James's Pull-ups and Aaron's Box Jumps

The final paragraph discusses James's butterfly chest to bar pull-ups and Aaron's box jumps, focusing on their frequency, energy expenditure, and power output. James performs 21 repetitions in 24 seconds, resulting in a frequency of 0.875 Hz and a duration of 1.14 seconds per pull-up. Aaron, weighing 500 Newtons, jumps onto a 0.6 m box 20 times in 52 seconds. Each jump requires 300 Joules of work, and the total energy expenditure for all jumps is 6,000 Joules. The average power output during the jumps is calculated as 115 Watts, determined by dividing the total work by the time. The paragraph concludes with a discussion on the net work done on Aaron, which is zero since there is no net displacement after the exercise.

Mindmap
Keywords
💡Work
In the context of the video, work refers to the physical quantity that represents the amount of effort exerted by a force on an object as it moves through a distance. It is calculated as the product of the force applied and the displacement in the direction of the force. For example, in the case of Tom performing thrusters, work is calculated as the force (441 Newtons) times the displacement (1.5 meters), resulting in 662 Joules of work done.
💡Energy
Energy is the capacity to do work, and it exists in various forms such as kinetic, potential, and mechanical energy. In the video, mechanical energy is often transformed into other forms, like gravitational potential energy when Heidi climbs the rope, and back into kinetic energy if she were to release the rope at the top. The conservation of energy principle is also highlighted, where the total amount of energy remains constant throughout the process.
💡Power
Power is the rate at which work is done or energy is transferred over time. It provides a measure of how quickly a task can be performed. In the video, the power developed during the exercises is calculated by dividing the work done by the time taken to perform the task. For instance, the power developed when lifting the barbell is calculated by dividing the work done (662 Joules) by the time (2 seconds), resulting in a power output of 331 Watts.
💡Force
Force is any action that can cause an object to accelerate or change its direction of motion. In the context of the video, force is applied by the individuals performing the exercises to overcome the weight of the barbell or their own body weight. The applied force must be equal to or greater than the weight (mass times gravity) to move the object upwards.
💡Displacement
Displacement is the change in position of an object and is a vector quantity that has both magnitude and direction. In the context of the video, displacement refers to the distance moved by the barbell, the person, or any object in question during the exercise, and it is used in the calculation of work done. It is important to note that displacement is different from distance traveled, as it takes into account the direction of movement.
💡Acceleration due to gravity
Acceleration due to gravity is the constant rate at which objects near the Earth's surface are pulled towards it, commonly denoted by 'g' and measured in meters per second squared (m/s^2). In the video, this value is used to calculate the weight of objects and individuals, which is then used to determine the force required to perform the exercises.
💡Gravitational potential energy
Gravitational potential energy is the energy an object possesses due to its position in a gravitational field, typically related to its height above a reference point like the ground. In the video, this concept is used to calculate the energy Heidi gains while climbing the rope and the energy she would have if she were to release the rope at the top.
💡Kinetic energy
Kinetic energy is the energy an object possesses due to its motion. It is directly proportional to the mass of the object and the square of its velocity. In the video, kinetic energy is discussed in the context of what Heidi would have if she were to release the rope at the top, which would be equal to the potential energy she had gained.
💡Net work
Net work is the total work done on an object when considering all forces acting on it. In the context of the video, it is emphasized that the net work done on the individuals at the end of their exercises is zero, as they return to their starting positions, and thus the total displacement is zero.
💡Frequency
Frequency is the number of times a specific event or cycle occurs within a given time period. In the video, frequency is used to describe how often the athletes perform their repetitions in the exercises, such as the number of pull-ups James can do in one second.
💡Velocity
Velocity is the speed of an object in a specific direction. It is a vector quantity that includes both magnitude and direction. In the context of the video, velocity is used to calculate the minimum speed required for Heidi to reach the top of the rope if she were to release it and for Aaron to reach the top of the box when jumping.
Highlights

Tom performs 10 thrusters with a 45 kg barbell in 20 seconds.

The applied force must match the weight of the barbell to move it upwards.

The force applied is at least equal to mg (441 Newtons).

Work done is calculated as force times displacement (662 Joules).

Power developed is the rate of work done (331 Watts).

Net work over the entire 20 seconds is zero since the bar ends up where it started.

Chris performs 20 toes to Bar exercises in 28 seconds.

The period of each toes to Bar exercise is 1.4 seconds.

Frequency is the inverse of the period (0.71 Hertz).

Heidi climbs 5 m up a rope three times in 40 seconds.

Heidi must apply a force equal to her weight (490 Newtons) to move upward.

Minimum work done by Heidi to climb the rope is 2450 Joules.

Heidi's gravitational potential energy at the top of the rope is 2450 Joules.

If Heidi releases the rope at the highest point, she would strike the ground with a velocity of 9.9 m/s.

James performs 21 butterfly chest to Bar pull-ups in 24 seconds.

James executes his pull-ups with a frequency of 0.875 Hertz.

Aaron jumps from the ground onto a 0.6 m box 20 times in 52 seconds.

Work done by Aaron in jumping onto the box is 300 Joules.

Aaron must expend a minimum energy of 300 Joules per jump.

For the 20 jumps, Aaron expends a total energy of 6000 Joules.

Average power expended by Aaron during the 20 jumps is 115 Watts.

Net work done on Aaron at the end of the exercise is zero.

Transcripts

Browse More Related Video

Work, Energy and Power in CrossFit Problems, Part 1

High School Physics - Work

High School Physics - Springs and Hooke's Law

2022 Live Review 3 | AP Physics C: Mechanics | Work, Energy, and Power

Work, Energy, and Power - Basic Introduction

Work Energy and Power Full Topic

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CrossFitWorkout AnalysisPhysics in FitnessExercise MechanicsStrength TrainingPower CalculationWork CalculationEnergy ExpenditureFitness EducationPerformance Optimization