What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var
TLDRThe transcript discusses the concept of an estimator in statistics, explaining it as a sample-based calculation used to estimate population parameters. It distinguishes between biased and unbiased estimators, emphasizing that an unbiased estimator has an expected value equal to the population parameter. The transcript provides examples, including the calculation of population mean (mu) using the sample mean (x bar), and the adjustment needed for the sample variance (s squared) to be an unbiased estimator. The explanation is clear, focusing on the importance of using the correct denominator (n-1) for variance estimation to achieve unbiased results.
Takeaways
- 📊 An 'estimator' in statistics is a calculated value derived from a sample that is used to estimate a population parameter.
- 🔢 The population is the entire set of items or data points of interest, which is often too large or impractical to observe in its entirety.
- 🎯 The sample is a smaller, manageable subset of the population that is actually observed and used for statistical analysis.
- 🧮 The population mean (μ) is a key parameter that can be estimated using the sample mean (x̄), calculated as the sum of sample values divided by the sample size (n).
- 📈 An 'unbiased estimator' is one whose expected value equals the true population parameter it is intended to estimate.
- 🌟 The expected value of an unbiased estimator is equal to the population parameter, which means that if multiple samples were taken and averaged, the result would converge to the true population value.
- 🔍 The expected value of the sample mean (x̄) is shown to be equal to the population mean (μ), confirming it as an unbiased estimator of the population mean.
- 📉 A biased estimator does not have its expected value equal to the population parameter, and an example given is the sample variance calculated using the wrong denominator.
- 🔄 The adjustment made to the sample variance formula (dividing by n-1 instead of n) is to ensure that the estimator is unbiased for the population variance.
- 🧬 The expected value of the biased sample variance (using n in the denominator) is shown to be equal to (n-1) times the population variance, rather than the population variance itself.
- 🔧 The correct calculation of sample variance, dividing by n-1, leads to an unbiased estimator of the population variance, which is a crucial concept in statistical analysis.
Q & A
What is an estimator in statistics?
-An estimator is a statistic used to estimate a population parameter based on a sample. It is a calculation derived from the sample data that provides an approximation of the unknown population characteristic.
Why can't we observe the entire population in statistics?
-In many cases, it is impractical, expensive, or impossible to observe every single member of a population. Therefore, we rely on sampling methods to collect data from a subset of the population and use that information to make inferences about the entire population.
How is the sample mean calculated?
-The sample mean, denoted as x-bar, is calculated by summing all sample values (x1, x2, ..., xn) and dividing the sum by the number of samples (n).
What is the expected value of a sample mean?
-The expected value of a sample mean is the average of all possible sample means that could be obtained from the same population. It is a theoretical concept that helps in understanding the central tendency of the sampling distribution of the mean.
What does it mean for an estimator to be unbiased?
-An estimator is unbiased if its expected value equals the true population parameter it is estimating. In other words, the average of all the estimates from multiple samples should be equal to the actual population parameter.
How can we show that the sample mean is an unbiased estimator of the population mean?
-Since the expected value of each xi is mu (the population mean), the expected value of the sum of xi's divided by n (which is the sample mean x-bar) is also mu. This is because the expected value of the sum is the sum of the expected values, and the division by n does not change this property.
What is the purpose of the adjustment 'n-1' in the calculation of sample variance?
-The adjustment 'n-1' is used in the calculation of sample variance to provide an unbiased estimate of the population variance. Without this adjustment, the estimator would be biased because it would underestimate the true variance due to the smaller sample size and the use of the sample mean in the calculation.
What is the expected value of the biased sample variance?
-The expected value of the biased sample variance (calculated as the sum of (xi - x-bar)^2 divided by n) is equal to the population variance (sigma squared) divided by n times (n-1), which is not equal to the true population variance (sigma squared).
How does the use of 'n-1' in the denominator correct the bias in the sample variance?
-Using 'n-1' in the denominator corrects the bias by accounting for the fact that the sample mean is used in the calculation of the variance. This adjustment gives more weight to the variability between individual observations and less weight to the variability due to the use of the sample mean, resulting in an unbiased estimate of the population variance.
What is the relationship between variance and the expected value?
-Variance is defined as the expected value of the squared deviation of a random variable from its mean. In other words, variance measures how much the values of a random variable deviate from their expected value (mean) on average.
How does the concept of an unbiased estimator contribute to the validity of statistical inferences?
-An unbiased estimator ensures that, on average, the estimates derived from samples will be equal to the true population parameters. This is crucial for the validity of statistical inferences because it means that our conclusions about the population are not systematically skewed or biased in any direction.
Outlines
📊 Introduction to Estimators
This paragraph introduces the concept of an estimator in statistics, explaining the fundamental idea of using a sample to make inferences about a population. It defines an estimator as a calculation derived from a sample that estimates an unknown population parameter. The paragraph also introduces the term 'unbiased', explaining that an unbiased estimator is one whose expected value equals the population parameter it is estimating. The example of the sample mean (x bar) as an unbiased estimator of the population mean (mu) is provided, with a brief explanation of how it is calculated and why it is considered unbiased.
🧮 Understanding Biased Estimators
This paragraph delves into the concept of biased estimators, contrasting them with unbiased ones. It starts by explaining how the sample variance (s squared) can be estimated and why the common formula includes a division by 'n-1' rather than 'n'. The paragraph then goes through a detailed mathematical derivation to show that using 'n' in the denominator leads to a biased estimator of the population variance (sigma squared). It concludes by highlighting the importance of using 'n-1' to obtain an unbiased estimator, emphasizing the need for this adjustment to get the correct expected value.
🔢 Mathematical Explanation of Biased Estimator
The paragraph provides a mathematical breakdown of why the standard estimator using 'n' in the denominator is biased. It begins by expressing the expected value of the squared deviations from the mean and proceeds to simplify this expression through algebraic manipulation. The explanation involves expanding the sum, applying the properties of expected values, and considering the definitions of variance and expected value. The paragraph concludes by showing that the expected value of the biased estimator does not equal the population variance, thus confirming its bias.
📉 Correcting Bias in Estimation
This paragraph concludes the discussion on biased estimators by explaining the correction factor 'n-1'. It reiterates the mathematical derivation from the previous paragraph, showing that using 'n-1' instead of 'n' in the denominator of the sample variance formula results in an unbiased estimator. The paragraph clarifies why the adjustment is necessary and how it leads to the correct expected value of the population variance (sigma squared). It reinforces the importance of using the correct formula to obtain unbiased estimates, which is crucial for accurate statistical analysis.
Mindmap
Keywords
💡estimator
💡population
💡sample
💡population parameter
💡unbiased estimator
💡expected value
💡variance
💡sample mean
💡sample variance
💡n-1
💡degrees of freedom
Highlights
An estimator is a method used in statistics to estimate population parameters based on a sample.
The population in statistics refers to the entire set of items or data points of interest, which are often unobservable in their entirety.
A sample is a subset of the population that is used to infer information about the whole population.
The population mean (mu) is a key parameter that can be estimated using a sample.
The sample mean (x bar) is calculated as the sum of all sample values divided by the number of samples (n).
An unbiased estimator is one where the expected value of the estimator equals the population parameter it is estimating.
The expected value of an estimator is the average of all possible sample means that could be obtained from the population.
The sample mean (x bar) is an unbiased estimator of the population mean (mu), as its expected value equals mu.
The concept of bias in estimation refers to the difference between the expected value of an estimator and the true population parameter.
Variance is a measure of the spread or dispersion of a set of values in a population or sample.
The sample variance (s squared) is calculated using the deviations of each sample value from the sample mean, squared and averaged.
An adjustment (n minus 1) is made in the denominator when calculating sample variance to achieve an unbiased estimator of the population variance.
The expected value of the sample variance calculated with n in the denominator is biased and does not equal the population variance.
The use of n minus 1 in the calculation of sample variance corrects the bias and results in an unbiased estimator of the population variance.
The concept of expected value is central to understanding unbiased estimators and their relationship to population parameters.
Statistical estimation relies on the properties of random samples to make inferences about unknown population parameters.
The theoretical underpinnings of unbiased estimators are crucial for valid statistical analysis and interpretation of results.
Transcripts
Browse More Related Video
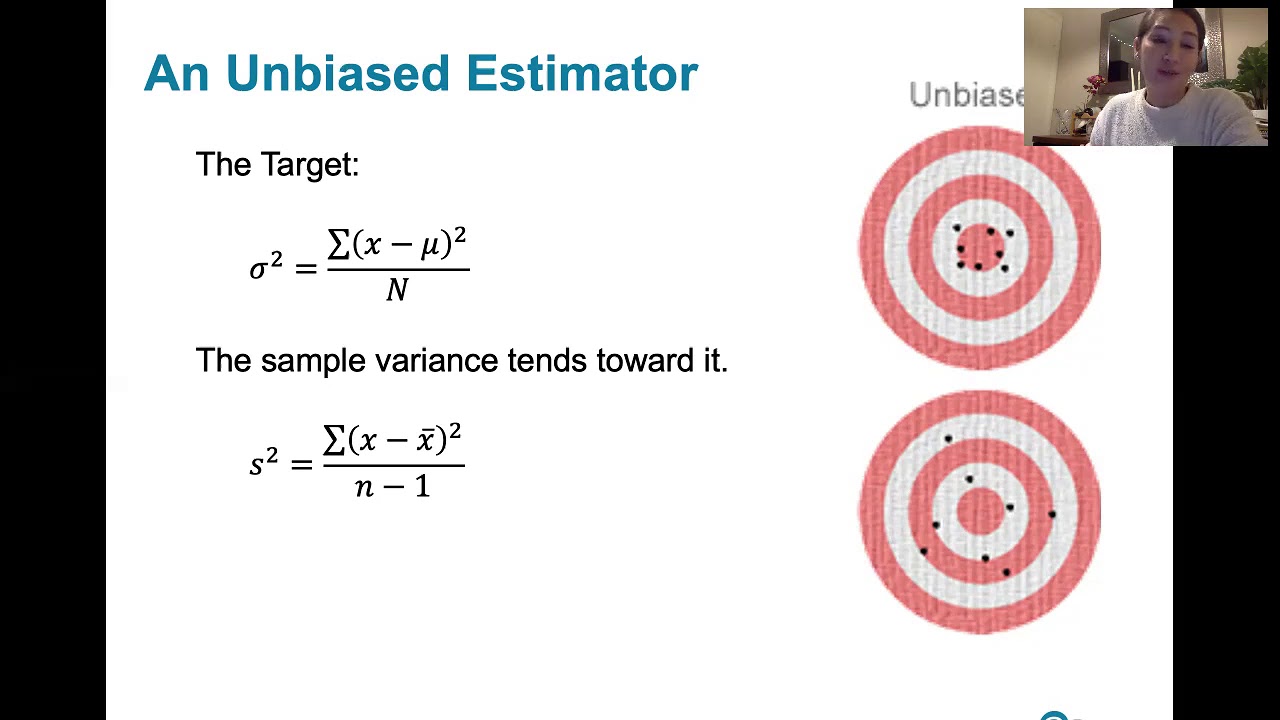
6.3.5 Sampling Distributions and Estimators - Biased and Unbiased Estimators
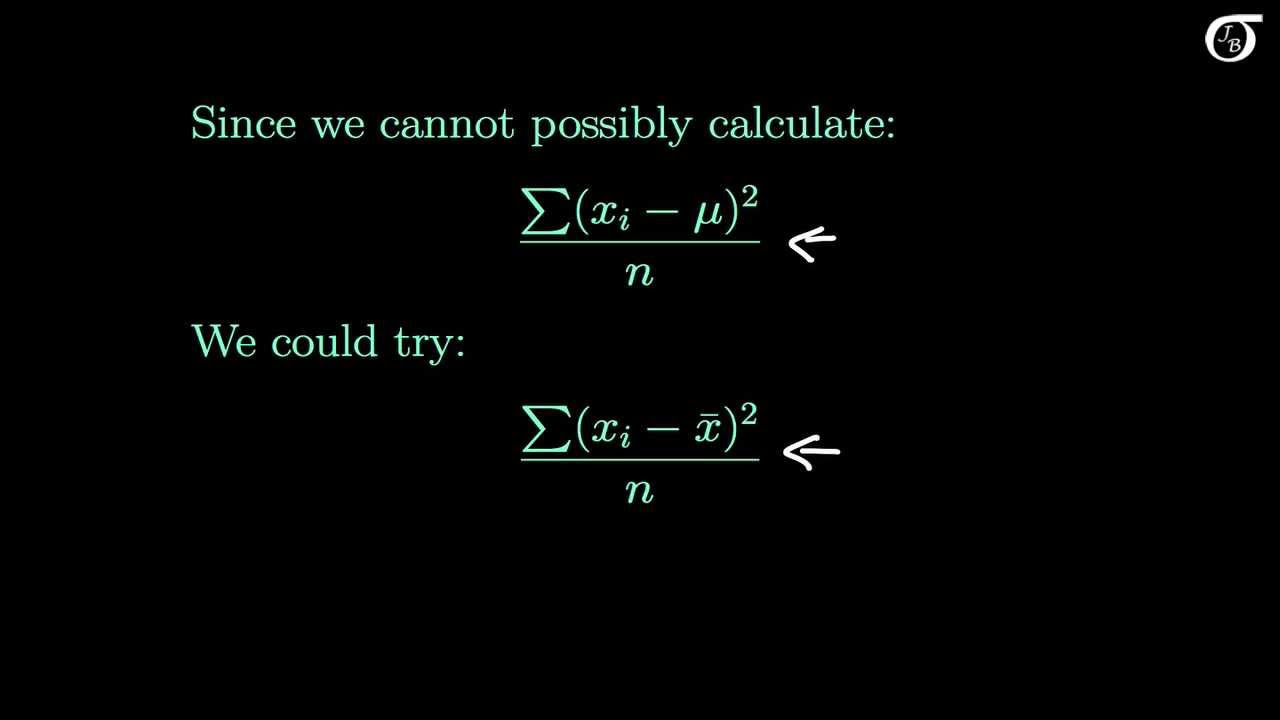
The Sample Variance: Why Divide by n-1?
Simulation showing bias in sample variance | Probability and Statistics | Khan Academy

6.3.4 Sampling Distribution and Estimators - Sampling Distribution of Sample Variance
Biased and unbiased estimators from sampling distributions examples
6.3.3 Sampling Distributions and Estimators - Sampling Distribution of the Sample Means
5.0 / 5 (0 votes)
Thanks for rating: