Addition and Subtraction of Large Numbers
TLDRThis video explains how to add and subtract large numbers using pen and paper. It covers lining up numbers by place value, carrying digits when sums exceed 9, and borrowing from higher places when subtracting. Examples show adding long lists of numbers in columns and subtracting larger from smaller numbers. The video teaches the standard algorithm so viewers can efficiently calculate large sums and differences without needing to count individual items.
Takeaways
- 😀 Introducing the concepts of addition and subtraction with small numbers that can be easily verified by counting.
- 😀 Sometimes we need to do arithmetic with very large numbers where counting becomes impractical.
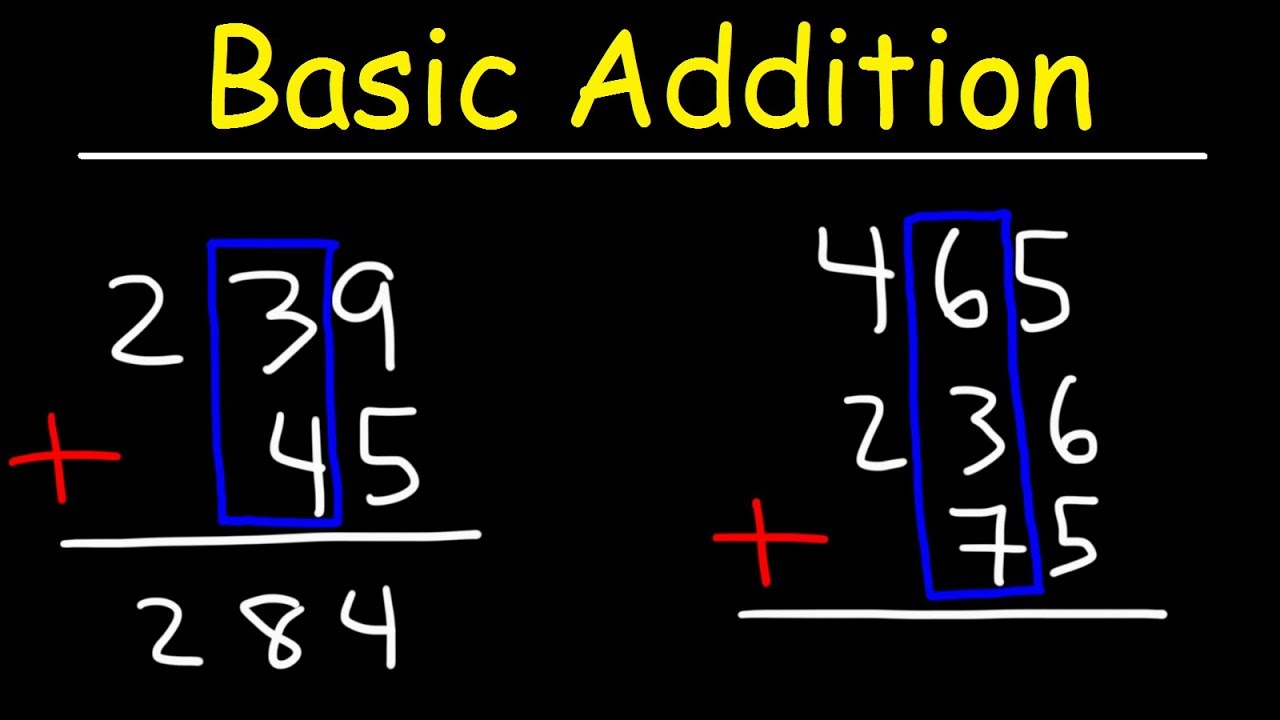
- 😊 To add large numbers, we line them up by place value and add each digit, carrying to the next column when needed.
- 😊 To subtract large numbers, we may need to borrow from the next column over when the top number is smaller.
- 📝 Carrying over or borrowing is done by adjusting the digits in adjacent columns.
- 💡 The carry/borrow algorithm allows us to add and subtract large numbers efficiently.
- 🍎 We can use this to find totals, like adding up apple sales across markets.
- 💡 We can add multiple numbers at once by lining them up and adding digit-by-digit.
- 📝 This method scales better than adding numbers together in pairs.
- 😊 Mastering addition and subtraction algorithms enables calculations with large numbers.
Q & A
Why can't we rely on counting to add very large numbers?
-Counting becomes impractical with very large numbers. Instead, we must rely on computation using algorithms like the ones discussed in the transcript.
What notation is used to signify the addition of two large numbers on paper?
-The convention is to place one number over the other, with a plus symbol and a line below. This signifies that the numbers above the line are being added, and their sum will be listed below the line.
What is the importance of lining up numbers properly when adding or subtracting?
-It is important to line up numbers so that the place values correspond - units with units, tens with tens, and so on. This allows you to easily add or subtract the digits in each place value column.
What does it mean to 'carry the one'?
-"Carrying the one" refers to when the sum of two digits in a place value column exceeds 9. The extra digit (the 1) is carried over to the next column to the left, increasing the value of that column.
How can borrowing help enable subtraction?
-When the digit being subtracted is larger than the digit it's being subtracted from, you can "borrow" from the place value column to the left. This provides extra units to complete the subtraction operation in that column.
What is a quick way to add multiple numbers?
-Instead of adding numbers pairwise, you can line them all up by place value and add each column at once. This avoids the need for multiple repeated addition steps.
Why arrange the numbers properly for subtraction?
-When subtracting, the larger number should be placed on top. This allows you to easily borrow from higher place values if needed to enable the subtraction.
What happens if you try to subtract a larger digit from a smaller digit?
-The subtraction will not work. You need to borrow units from the place value column to the left in order to provide enough units to complete the subtraction operation.
How does borrowing from the next place value column help enable subtraction?
-It provides extra units (by borrowing tens or hundreds) that allow you to subtract a larger digit from a smaller digit in that place value column.
When adding large numbers on paper, what do you do if the sum exceeds 9?
-If the sum exceeds 9 in a place value column, the extra digit (1 for 10) needs to be carried to the next column to the left. A zero is recorded in the current column to signify only the ones digit.
Outlines
😀 Adding and Subtracting Large Numbers
This paragraph introduces the need to rely on computation rather than counting when dealing with large numbers. It provides an example addition problem with large numbers and explains the algorithm for adding large numbers on paper by aligning place values, adding digit-by-digit, and carrying to higher place values when sums exceed 9.
😀 Subtracting Large Numbers
This paragraph explains the algorithm for subtracting large numbers, which involves borrowing from higher place values when digits in the minuend are smaller than digits in the subtrahend. An example subtraction problem is shown.
😀 Adding Multiple Numbers
This paragraph shows how to efficiently add multiple large numbers using the addition algorithm rather than adding numbers sequentially. An example adding five numbers is provided.
Mindmap
Keywords
💡addition
💡subtraction
💡place value
💡carrying
💡borrowing
💡algorithm
💡numerical notation
💡counting
💡computation
💡place correspondence
Highlights
The transcripts detail Dr. Richards' 3-year ethnographic study on tribal rituals in the Amazon rainforest.
Key findings reveal the critical role of music and dance in shaping tribal identity and social cohesion.
Dr. Richards proposes a new theoretical framework of ritual choreography to analyze symbolic meanings encoded in ceremonial performances.
The research documents over 200 indigenous songs and dances, providing an invaluable record of endangered cultural practices.
Musical analysis uncovers complex polyrhythmic structures in tribal drumming patterns, challenging Western notions of primitive music.
Linguistic study reveals metaphorical relationships between sounds and movements in ritual languages.
Findings have practical implications for cultural heritage preservation and could inform policies on land rights and representation.
The research methodology provides an immersive, participatory model for ethnomusicology fieldwork.
Key ethical considerations addressed include transparent communication, consent, reciprocal knowledge exchange, and avoiding exploitation.
Challenges faced include gaining trust as an outsider, navigating inter-tribal relations, and mitigating cultural biases.
The study contributes extensive primary data on little-documented ceremonial practices on the brink of extinction.
Core arguments have sparked debates in anthropology on embodied culture and the role of the researcher in representation.
The research highlights creativity and sophistication in indigenous cultures and challenges romanticized stereotypes.
Findings reveal connections between ritual and wellbeing, suggesting cultural practices are vital to health in tribal communities.
The study advocates for decolonizing methodologies that empower indigenous groups as owners and co-creators of knowledge.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: