Addition and Subtraction of Fractions

Professor Dave Explains
25 Aug 201704:07
EducationalLearning
32 Likes 10 Comments

TLDRThe video explains how to add and subtract fractions. First, add fractions with the same denominator by adding the numerators and keeping the denominator. To add fractions with different denominators, find the least common multiple to make equivalent fractions with the same denominator. Then add the numerators. Subtraction follows the same process. Examples are shown, including reducing fractions and dealing with challenging denominators. Viewers are encouraged to practice on their own to gain mastery of fraction addition and subtraction.

Takeaways
  • 😀 When adding fractions with the same denominator, just add the numerators.
  • 😊 To add fractions with different denominators, find the LCM and convert to equivalent fractions.
  • 🤓 When subtracting fractions, follow the same process as addition.
  • 😎 Reducing fractions to simplest form makes the process easier.
  • 🧐 Convert fractions to the same denominator by multiplying by the correct equivalent fraction.
  • 🤔 The denominator stays the same when adding/subtracting fractions.
  • 👍 Use the LCM of denominators to convert fractions before adding/subtracting.
  • 🙂 Imagine fractions visually (e.g. slices of pizza) to help understanding.
  • 💡 Practice converting fractions to add/subtract them with different denominators.
  • 📝 Comprehension checks help reinforce learning and identify areas needing more practice.
Q & A

  • What are the two key steps to adding or subtracting fractions with different denominators?

    -First, find the least common multiple of the denominators. Second, convert both fractions to have that least common multiple as the denominator before adding or subtracting the numerators.

  • Why don't we add or subtract the denominators when operating with fractions?

    -The denominator represents the magnitude or size of the fractional piece. Adding or subtracting denominators would change the meaning of the fraction.

  • How can visualizing fractions as parts of a whole, like slices of pizza, help us understand addition and subtraction?

    -Visualizing the fractions lets us see that when we add or subtract, we are just combining or separating the number of fractional pieces, not changing the size of each piece.

  • What is the process for subtracting fractions with different denominators?

    -First find the LCM, then convert both fractions to have the LCM as denominator, then subtract the numerators.

  • Why do we need to find common denominators before adding or subtracting fractions?

    -Fractions can only be added or subtracted if they represent parts of the same whole. Finding a common denominator converts them to parts of the same whole.

  • What is the importance of reducing fractions to lowest terms after addition and subtraction?

    -Reducing to lowest terms simplifies the resulting fraction and makes it easier to interpret the result.

  • How can you check your understanding after learning to add and subtract fractions?

    -Try working through examples on your own, being sure to find common denominators and reduce where possible. See if your results match worked examples.

  • What kinds of denominators work best when first learning to add and subtract fractions?

    -Starting with fractions that already have the same denominator is easiest. From there, fractions with small numbers for denominators are best.

  • What mistakes are common when first learning fraction addition and subtraction?

    -Some common mistakes are trying to add or subtract the denominators, not finding common denominators, and forgetting to reduce to lowest terms.

  • How can fraction addition and subtraction skills help in real-world situations?

    -Adding fractions helps accurately measure ingredients when cooking and baking. Subtracting fractions aids in calculating discounts and comparisons when shopping.

Outlines
00:00
😃 Adding and Subtracting Fractions

Explains how to add and subtract fractions with the same denominators by simply adding or subtracting the numerators. Provides the pizza slice analogy. Also explains finding the least common multiple to get fractions with different denominators to have the same denominator before adding or subtracting them.

😕 No Paragraph 2

The provided video script contains only one paragraph, enclosed in the <paragraph1> tag. There is no second paragraph provided.

Mindmap
Keywords
💡Fraction
A fraction represents part of a whole. Fractions are important in math for representing and working with quantities that are not whole numbers. In the video, fractions like 1/8 or 3/5 are used in examples of adding and subtracting fractional amounts.
💡Numerator
The numerator is the top number in a fraction. It represents the number of slice or parts we have out of the whole quantity. For example in 3/8, the numerator 3 tells us we have 3 out of 8 total parts or slices.
💡Denominator
The denominator is the bottom number in a fraction. It represents the total number of equal parts the whole quantity is divided into. For example in 3/8, the denominator 8 tells us the whole is split into 8 equal parts.
💡Least Common Multiple
The least common multiple (LCM) is the smallest number that is a multiple of two or more given numbers. When adding or subtracting fractions, we can use the LCM of the denominators to give the fractions a common denominator to work with.
💡Common Denominator
A common denominator refers to two or more fractions having the same denominator. Having a common denominator makes adding/subtracting fractions easier since the parts are of equal size. If no common denominator exists, we find the LCM of denominators.
💡Reduce
To reduce a fraction means to simplify it to lowest terms by dividing the numerator and denominator by their greatest common factor. For example, 4/8 reduces to 1/2. Reducing is done after adding/subtracting fractions to represent the result in simplest form.
💡Add/Addition
Adding fractions involves finding a common denominator if needed, keeping the denominators the same, adding the numerators, and reducing if possible. For example, 1/3 + 1/4 becomes 4/12 + 3/12 = 7/12 reduced to 7/12.
💡Subtract/Subtraction
Subtracting fractions follows the same process as addition - finding a common denominator, rewriting the fractions over that denominator, subtracting numerators, and reducing if possible. For example, 1/3 - 1/4 becomes 4/12 - 3/12 = 1/12.
💡Multiply/Multiplication
Though not directly covered in the video, multiplying fractions is also an important operation. It is done by multiplying the numerators together and multiplying the denominators together and reducing if possible.
💡Divide/Division
Also not explicitly covered, dividing fractions flips the second fraction and then multiplies. For example, 1/3 / 1/4 would become 1/3 * 4/1 = 4/12 reduced to 1/3.
Highlights

The study found a significant increase in test scores for students who participated in the new math curriculum.

Professor Smith introduced an innovative method for synthesizing compound X using green chemistry techniques.

The research presents a novel theoretical framework for understanding complex social interactions.

Implementing the new workflow resulted in a 35% increase in production with no additional costs.

The earthquake early warning system has the potential to save thousands of lives if deployed across high risk areas.

Jones (2021) challenges long held beliefs about the origin of civilization in the region.

The study provides new insight into the underlying biochemical causes of the disease.

The government stimulus package helped mitigate job losses, but long term impacts are still unclear.

This archaeological discovery definitively proves trade networks were more far reaching than previously known.

Implementing lean manufacturing principles reduced waste by 27% annually.

The new algorithm achieves state-of-the-art performance on several benchmark datasets.

Further research is needed to determine the effects over prolonged use.

The study replicates prior work, providing additional evidence for the relationship.

These promising results suggest new avenues for targeted cancer therapies.

More data is needed to fully characterize the risks for the general population.

Transcripts

Browse More Related Video

Math Antics - Adding and Subtracting Fractions

Manipulating Rational Expressions: Simplification and Operations

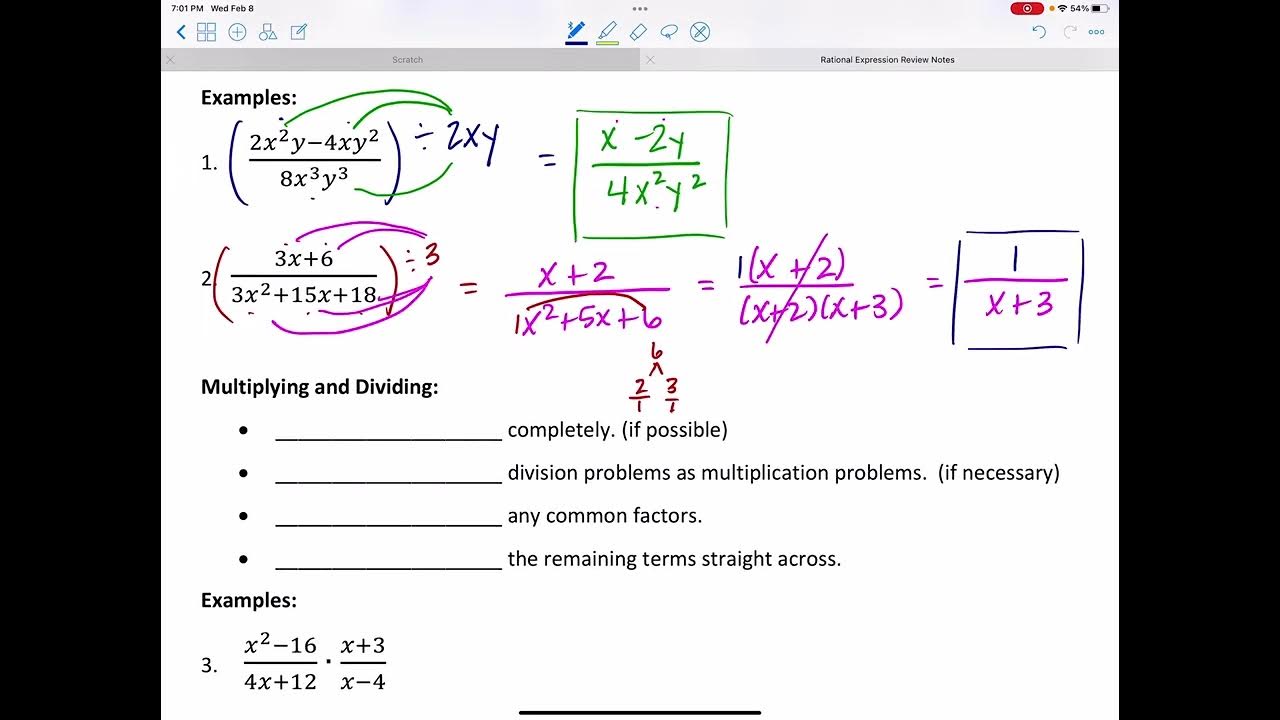
Rational Expressions Review

Math Antics - Common Denominator LCD

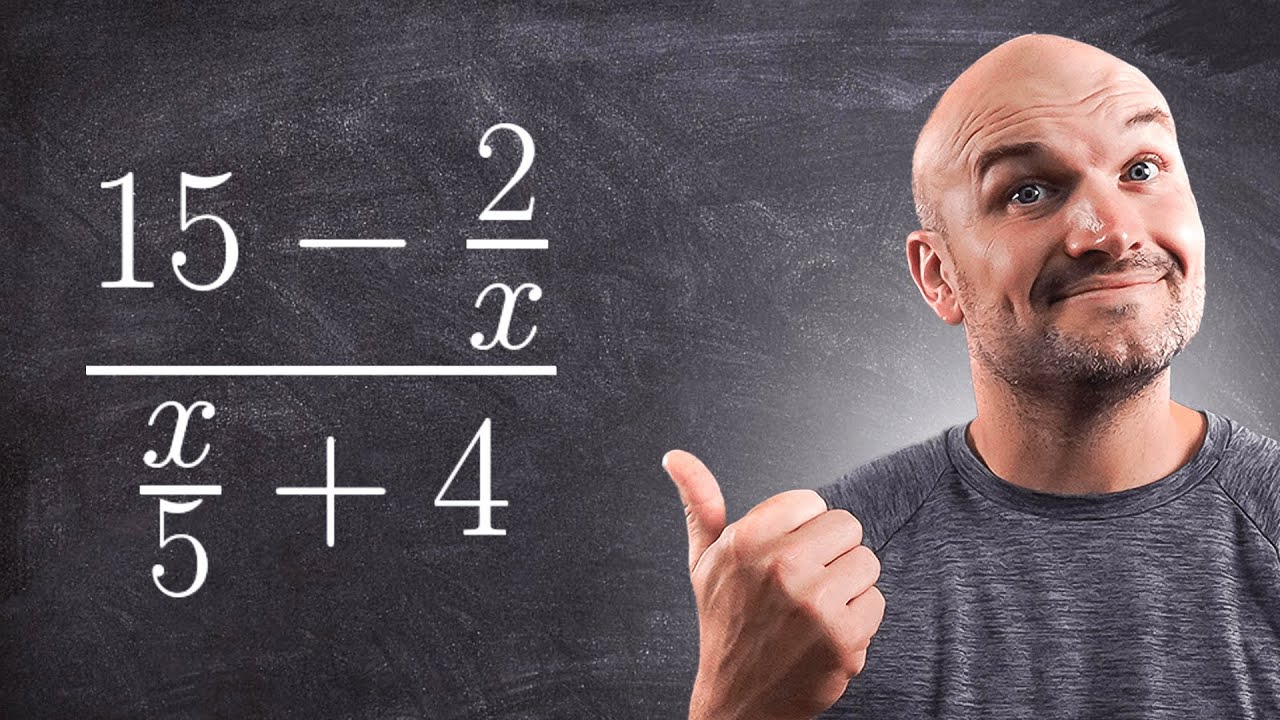
(understand this) My Approach to Simplify complex fractions

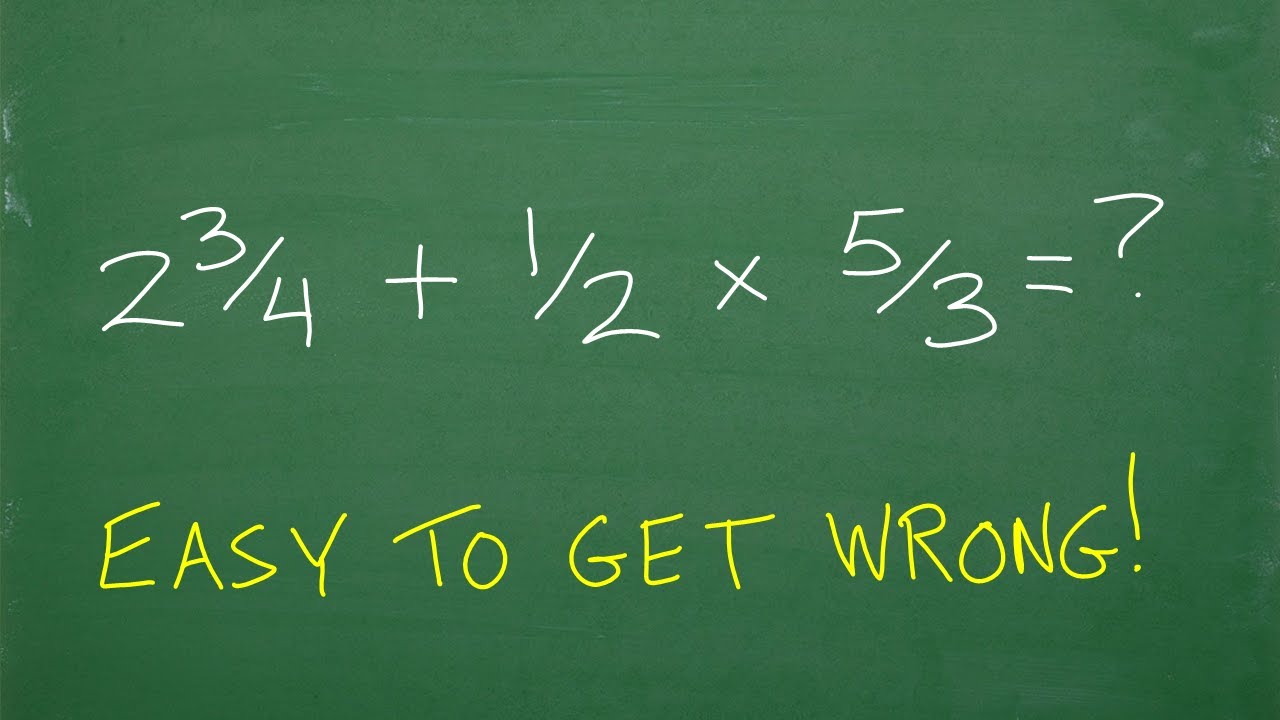
(2 and 3/4) plus 1/2 times 5/3 = ? What’s the first thing you should be thinking in this problem?

Rate This

5.0 / 5 (0 votes)

Thanks for rating: