6.3.5 Sampling Distributions and Estimators - Biased and Unbiased Estimators

Sasha Townsend - Tulsa
25 Oct 202012:48
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of biased and unbiased estimators, revisiting the topic with a focus on discrete and continuous probability distributions. It explains that an estimator is biased if its sample statistic values do not consistently target the population parameter, while an unbiased estimator's mean sampling distribution equals the population parameter. The video provides examples of each, such as the sample variance being an unbiased estimator of the population variance, and the sample standard deviation being a biased estimator of the population standard deviation. It also touches on the central limit theorem in the next lesson.

Takeaways
  • πŸ“š The video revisits the concepts of biased and unbiased estimators introduced in Chapter 3, focusing on their application in the context of discrete and continuous probability distributions.
  • πŸ” An estimator is a statistic used to estimate the value of a population parameter, and it is considered biased if its sample values do not target the population parameter's value.
  • 🎯 An unbiased estimator is one where the mean of the sampling distribution of the statistic equals the corresponding population parameter.
  • πŸ“‰ The sample variance is an example of an unbiased estimator of the population variance, calculated with n-1 in the denominator to account for degrees of freedom.
  • πŸ“Š The sample mean (x-bar) and sample proportion (p-hat) are also unbiased estimators, targeting the population mean (mu) and population proportion, respectively.
  • πŸ“ˆ The concept of 'targeting' refers to the mean of the sampling distribution of a statistic aligning with the population parameter it aims to estimate.
  • 🚫 Biased estimators, such as the sample median and sample range, do not target the corresponding population parameters when calculating their means from sampling distributions.
  • πŸ“Œ The sample standard deviation is a biased estimator of the population standard deviation, consistently underestimating the true value.
  • πŸ”’ The units of the sample variance (squared units of the original values) make it an unbiased estimator, despite being less intuitive than the standard deviation.
  • 🌐 The video emphasizes the importance of understanding the properties of different estimators, such as bias, in the context of statistical inference.
  • πŸ“š The next topic to be discussed is the central limit theorem, which is foundational in understanding the distribution of sample means.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is the difference between biased and unbiased estimators in the context of statistical learning, specifically from lesson 6.3.

  • What is an estimator in statistics?

    -An estimator is a statistic used to infer or estimate the value of a population parameter. It is derived from a sample and is used to make inferences about the population.

  • What makes an estimator biased according to the script?

    -An estimator is biased if the values of the sample statistic do not target the value of the corresponding population parameter, meaning the mean of the sampling distribution of the sample statistic is not equal to the population parameter.

  • What is an unbiased estimator?

    -An unbiased estimator is one where the values of the sample statistic do target the corresponding population parameter, with the mean of the sampling distribution of the sample statistic being equal to the population parameter.

  • Why is the sample variance considered an unbiased estimator of the population variance?

    -The sample variance is considered an unbiased estimator of the population variance because when all possible samples of the same size are taken from the population, and the sample variance is computed each time, the mean of all those sample variances is equal to the population variance.

  • What is the formula for calculating the sample variance and why is n-1 used in the denominator?

    -The sample variance is calculated by taking the mean of the sample (xΜ„), subtracting it from each x value in the sample, squaring the result, summing these squared differences, and then dividing by n-1 (n minus one). The n-1 is used because of the degrees of freedom in the sample; with n values, you can choose n-1 values before the last one is determined.

  • What are some examples of unbiased estimators mentioned in the script?

    -Examples of unbiased estimators mentioned in the script include the sample proportion (p-hat), the sample mean (x-bar), and the sample variance (s^2).

  • What are some examples of biased estimators discussed in the script?

    -Examples of biased estimators discussed in the script include the sample median, the sample range, and the sample standard deviation.

  • Why is the sample standard deviation considered a biased estimator of the population standard deviation?

    -The sample standard deviation is considered a biased estimator of the population standard deviation because when the mean of the sampling distribution of the sample standard deviations is computed, it consistently underestimates the population standard deviation.

  • What is the difference between the sample standard deviation and the sample variance in terms of bias?

    -The sample standard deviation is a biased estimator of the population standard deviation because it consistently underestimates it. On the other hand, the sample variance is an unbiased estimator of the population variance as its mean in the sampling distribution equals the population variance.

  • What is the significance of the sample mean being an unbiased estimator of the population mean?

    -The significance of the sample mean being an unbiased estimator of the population mean is that if you compute the mean of all possible sample means from samples of the same size, you actually get the population mean, making it a reliable estimator for the population parameter.

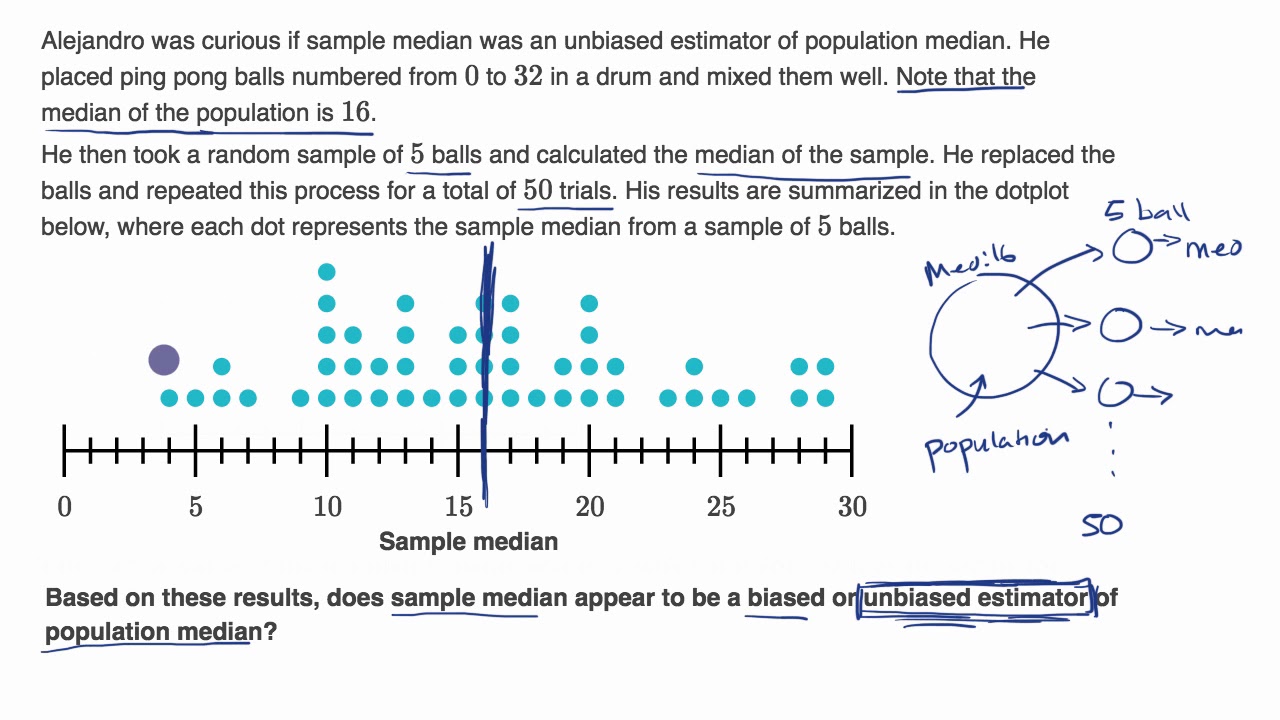
  • Why might the sample median be a biased estimator of the population median?

    -The sample median may be a biased estimator of the population median because when you compute the median for each sample and then find the mean of these medians, it does not necessarily yield the population median, indicating a bias.

Outlines
00:00
πŸ“Š Understanding Biased and Unbiased Estimators

This paragraph introduces the concept of biased and unbiased estimators, revisiting the topic previously discussed in chapter 3. It explains that an estimator is a statistic used to estimate a population parameter and is considered biased if its sample values do not target the population parameter's value. Conversely, an estimator is unbiased if its sample values do target the population parameter. The paragraph also clarifies the meaning of 'targeting' by stating that an estimator targets a parameter if the mean of its sampling distribution equals the population parameter. The explanation includes examples of sample statistics such as variance, standard deviation, mean, proportion, range, and median, and discusses the formula for calculating sample variance, emphasizing the importance of using n-1 in the denominator for an unbiased estimate of the population variance.

05:00
🎯 Examples of Unbiased and Biased Estimators

The second paragraph delves deeper into the characteristics of unbiased estimators, providing examples such as the sample proportion (p-hat), the sample mean (x-bar), and the sample variance, which are all unbiased because their sampling distributions' means equal the respective population parameters. It contrasts these with biased estimators like the sample median and range, which do not target the population median or range, respectively. The paragraph also highlights that the sample standard deviation is a biased estimator of the population standard deviation, as it consistently underestimates it. The explanation includes visual representations to illustrate how unbiased estimators are evenly distributed around the target value, whereas biased estimators are systematically off-target.

10:01
πŸ” The Implications of Bias in Estimators

The final paragraph discusses the implications of using biased estimators, focusing on the sample standard deviation as an example. It points out that while the sample standard deviation is easy to interpret due to its same units as the original data, it is a biased estimator because the mean of its sampling distribution is consistently less than the population standard deviation. The paragraph also reiterates the benefits of using unbiased estimators like the sample proportion, mean, and variance, which, when averaged over all possible samples of the same size, yield the exact population parameters. The summary concludes with a preview of the next topic, the central limit theorem, which will be discussed in the subsequent video.

Mindmap
Keywords
πŸ’‘Estimator
An estimator is a sample statistic that is used to infer or estimate the value of a population parameter. In the context of the video, it is a fundamental concept that differentiates between biased and unbiased estimators. For example, the script mentions that an estimator is biased if the sample statistic does not target the population parameter, as seen when discussing the sample standard deviation and sample variance.
πŸ’‘Biased Estimator
A biased estimator is one where the values of the sample statistic systematically deviate from the true value of the corresponding population parameter. The video script explains that the sample median, range, and standard deviation are examples of biased estimators because their means do not target the population median, range, or standard deviation, respectively.
πŸ’‘Unbiased Estimator
An unbiased estimator is a sample statistic whose mean, when considering all possible samples of the same size, equals the population parameter it is estimating. The script provides examples such as the sample proportion (p-hat), sample mean (x-bar), and sample variance (s^2), which are unbiased estimators of the population proportion, mean, and variance.
πŸ’‘Population Parameter
A population parameter is a numerical value that describes a characteristic of an entire population. In the video, the script discusses how estimators are used to estimate these parameters, such as the population mean (mu), population variance (sigma squared), and population standard deviation.
πŸ’‘Sample Statistic
A sample statistic is a value calculated from a sample that is used to estimate a population parameter. The script explains that sample statistics like the sample mean, variance, and standard deviation are used to infer information about the population from which the sample was drawn.
πŸ’‘Sample Variance
Sample variance is a measure of the dispersion of a set of data points in a sample, calculated as the average of the squared differences from the sample mean. The script emphasizes that the sample variance is an unbiased estimator of the population variance when using n-1 in the denominator.
πŸ’‘Sample Standard Deviation
The sample standard deviation is a measure of the amount of variation or dispersion in a set of values. The script points out that while the sample standard deviation is easy to interpret, it is a biased estimator of the population standard deviation because it consistently underestimates it.
πŸ’‘Sample Mean
The sample mean, denoted as x-bar in the script, is the average of the values in a sample. It is an unbiased estimator of the population mean (mu), as the mean of all possible sample means from samples of the same size will equal the population mean.
πŸ’‘Sample Proportion
The sample proportion, represented as p-hat, is the ratio of the number of successes to the number of trials in a sample. The script explains that the sample proportion is an unbiased estimator of the population proportion, meaning that the mean of all possible sample proportions will equal the actual population proportion.
πŸ’‘Sampling Distribution
A sampling distribution is the probability distribution of a given sample statistic when the sampling is repeated many times. The script discusses how the mean of the sampling distribution of an unbiased estimator will be equal to the population parameter, which is a key concept in understanding the properties of estimators.
Highlights

The video discusses learning outcome number five from lesson 6.3, focusing on the difference between biased and unbiased estimators.

The lesson revisits biased and unbiased estimators in the context of understanding discrete and continuous probability distributions.

An estimator is defined as a statistic used to estimate the value of a population parameter.

A biased estimator is one where sample statistic values do not target the corresponding population parameter.

Examples of sample statistics include the sample variance, standard deviation, mean, proportion, range, and median.

The concept of 'targeting' a population parameter means the mean of the sampling distribution of the statistic equals the population parameter.

Unbiased estimators are those where the mean of the sampling distribution targets the corresponding population parameter.

The sample variance is an unbiased estimator of the population variance when using n-1 in the denominator.

The unbiased nature of the sample variance is demonstrated through its sampling distribution mean equating to the population variance.

Other unbiased estimators include the sample proportion, sample mean, and sample variance.

Unbiased estimators are valuable as their sampling distribution means accurately reflect the population parameters.

Biased estimators, such as the sample median and range, do not target the corresponding population parameters.

The sample standard deviation is a biased estimator as it consistently underestimates the population standard deviation.

The use of variance as an unbiased estimator is contrasted with the sample standard deviation, which is easier to interpret but biased.

The lesson concludes with the understanding that unbiased estimators provide the exact population parameter when considering their sampling distribution means.

The video will continue in the next part with a discussion on the central limit theorem.

Transcripts

Browse More Related Video

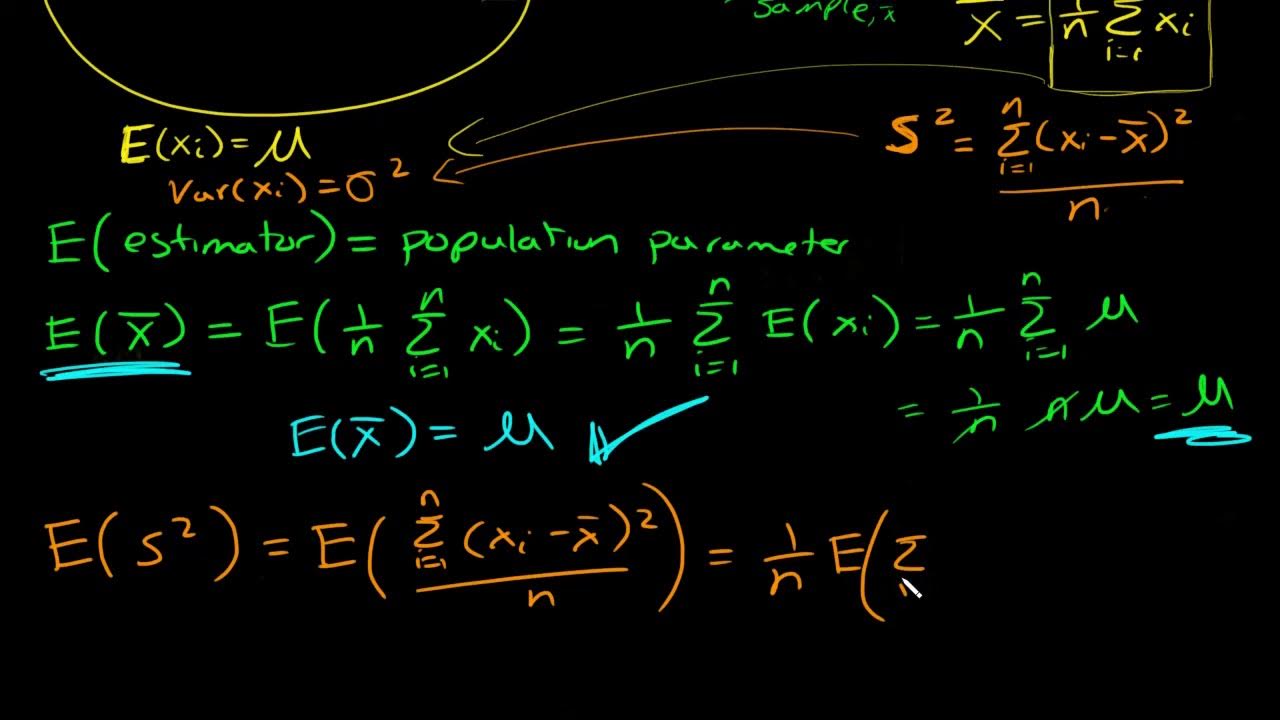
What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var

[6.3.7] Creating a variance sampling distribution probability distribution table in StatCrunch

Biased and unbiased estimators from sampling distributions examples

Simulation showing bias in sample variance | Probability and Statistics | Khan Academy

6.3.1 Sampling Distributions and Estimators - Sampling Distributions Described and Defined

Math 14 HW 6.3.7-T Is the sample variance an unbiased estimator of the population​ variance?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistics LearningEstimator TypesBiased EstimatorsUnbiased EstimatorsSample VariancePopulation VarianceSample Standard DeviationSampling DistributionsStatistical InferenceData AnalysisProbability Distributions