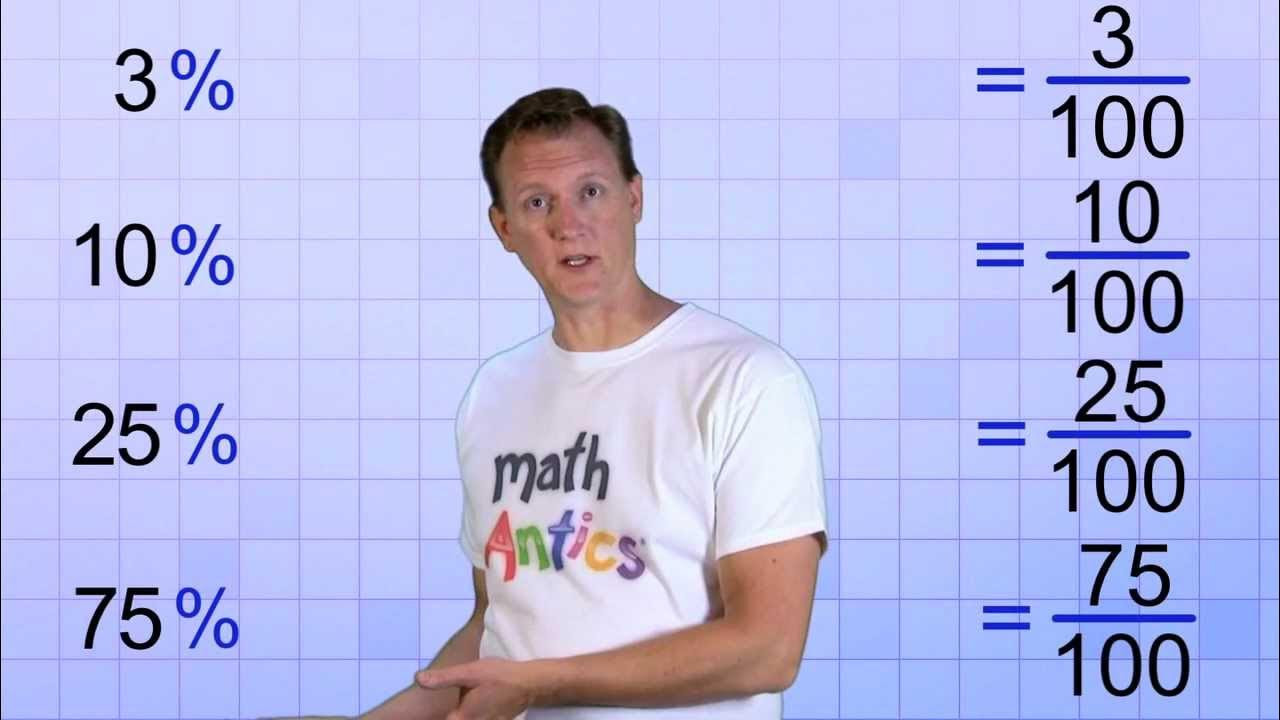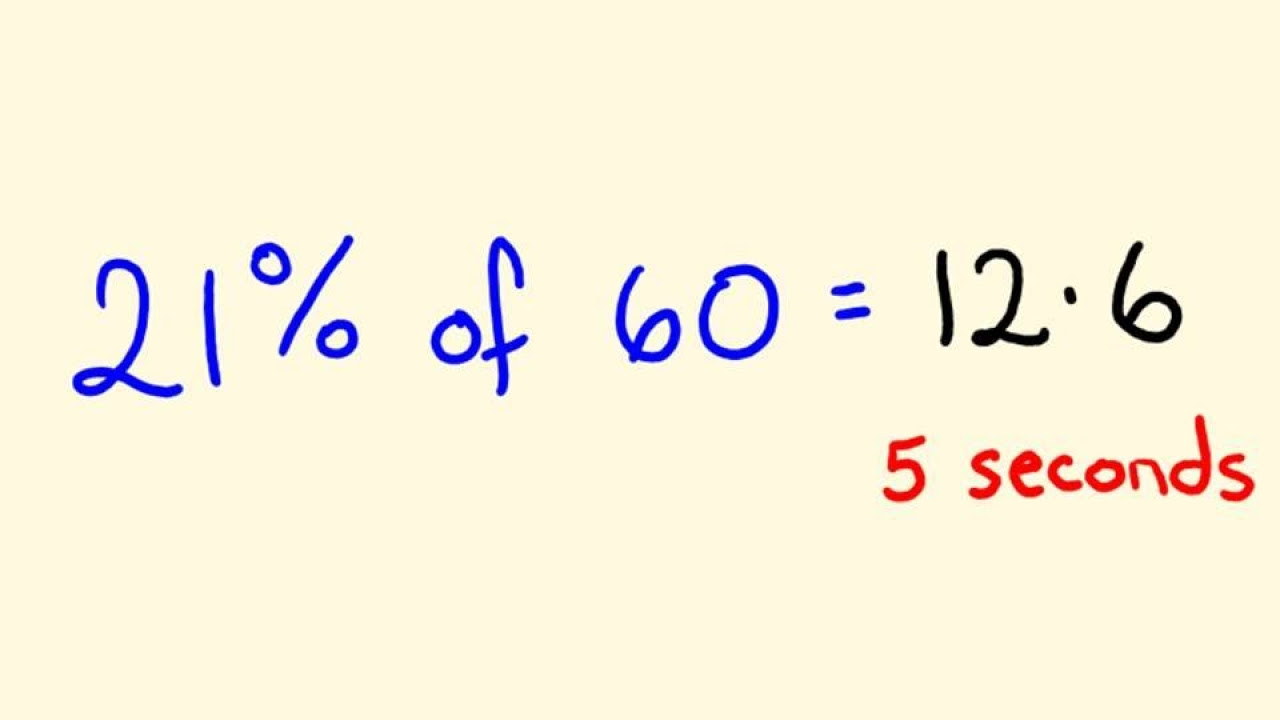Working With Percentages
TLDRThis video explains what percentages are and how they work. Percentages are ratios that compare a number to one hundred. One hundred is an ideal reference point because it is easy to comprehend yet has enough gradations for meaningful comparisons. Percentages can be converted to fractions by making the denominator one hundred. Fractions can then be simplified or converted to decimals. This allows easy conversion between percentages, fractions, and decimals. Examples are provided showing how to convert percentages like eighty percent and fifty percent into equivalent fractions and decimals. Viewers are then prompted to practice these percentage conversions themselves.
Takeaways
- 😀 Percent means out of 100, so percentages are ratios comparing numbers to 100.
- 😊 They compare to 100 because it's easy to understand but has enough gradations for comparisons.
- 🤓 80% equals 80/100 which can be simplified to 4/5.
- 🧐 50% is 50/100 which equals 1/2.
- 🤔 3% is 3/100 which can't be simplified further.
- 😎 We can convert between percentages, fractions and decimals easily.
- 🥸 A percentage is a fraction with denominator 100.
- 😇 100 is used as it's easy to understand and has enough gradations.
- 🤠 Percentages allow us to convey magnitude relative to 100.
- 😉 They provide a standard way to compare values.
Q & A
What does the term 'percent' literally mean?
-The term 'percent' literally means 'out of a hundred'. It comes from the Latin word 'centum', meaning one hundred.
Why is 100 considered an ideal number for comparison with percentages?
-100 is considered an ideal number for comparison because it is small enough that our brains can easily comprehend its magnitude, but also large enough that there are sufficient gradations between 0 and 100 to allow for meaningful comparisons.
If you scored 90 out of 100 on a test, what percentage is that?
-If you scored 90 out of 100 on a test, that is equal to 90%, because 90 is 90 out of the total 100.
What do percentages allow us to do?
-Percentages allow us to convey the magnitude or proportion of something relative to a total of 100. They modify some total into a hundred and report a value of interest as a fraction of that 100.
How can you convert a percentage to a fraction?
-To convert a percentage to a fraction, set the percentage over 100 reduced to its lowest terms. For example, 80% becomes 80/100, which reduces to 4/5.
True or false: 50% and 1/2 mean the same thing
-True. 50% is equal to 50/100, which reduces to 1/2. So 50% and 1/2 are equivalent fractions.
If you have 7 out of 25 on a quiz, what percentage is that?
-If you have 7 out of 25 on a quiz, first recognize that 25 needs to become 100. So multiply both numbers by 4. That gives you 7 * 4 = 28 and 25 * 4 = 100. 28 out of 100 is equal to 28%, so 7 out of 25 is equal to 28%.
Why are percentages considered ratios?
-Percentages are considered ratios because they compare two numbers, one to a hundred. They express one number as a fraction of another, specifically fractions with 100 in the denominator.
Can every percentage be converted to a fraction?
-Yes, every percentage can be converted to a fraction having 100 as the denominator. Simply place the percentage over 100 and simplify if possible.
What are some examples of using percentages in everyday life?
-Examples include sales discounts like 30% off, tips at restaurants like 20%, chances of precipitation like 50% chance of rain, and test scores like getting 90% of questions right.
Outlines
😀 Understanding Percentages
This paragraph introduces percentages, explaining that they are ratios that compare values to 100. It states that 100 is an ideal benchmark for comparison since it's small enough to easily comprehend yet large enough for meaningful gradations. The paragraph also notes that percentages can be converted to fractions and decimals.
😀 Comprehending the Response
This paragraph checks the reader's comprehension regarding the ability to convert between percentages, fractions, and decimals.
Mindmap
Keywords
💡percent
💡ratio
💡fraction
💡decimal
💡magnitude
💡arbitrary
💡simplify
💡equivalent
💡convert
💡comprehension
Highlights
Using neural networks to predict protein folding can revolutionize drug discovery.
The new algorithm significantly outperforms previous methods in protein structure prediction.
This research enables more accurate computational modeling of protein interactions.
Deep learning techniques are being applied to predict the 3D structure of proteins.
Understanding protein folding is key to developing new pharmaceuticals.
Predicting protein structures reduces the need for expensive lab experiments.
The model was trained on a large dataset of known protein structures.
This breakthrough will accelerate the pace of drug discovery.
The next step is testing the algorithm on complex protein formations.
The method can be applied to model protein interactions in human cells.
Understanding protein folding may shed light on diseases like Alzheimer's.
This research highlights the potential of AI for biomedical applications.
Collaboration between computer scientists and biologists was key.
The findings represent an important milestone in computational biology.
Further refinement of the technique is needed before real-world use.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: