More limits | Limits | Differential Calculus | Khan Academy
TLDRThe video script discusses the concept of limits in calculus, focusing on problems involving absolute values and squaring functions. The presenter walks through the process of solving limits from both the positive and negative sides of zero, emphasizing the importance of consistency in the results for the limit to exist. By using examples and substitutions, the video demonstrates how to simplify and evaluate complex limit expressions, ultimately confirming the results through graphing and numerical approximations.
Takeaways
- 📝 The main focus of the transcript is on solving limit problems involving absolute values and trigonometric functions as x approaches 0.
- 🤔 The challenge with absolute values lies in their non-linear nature, which complicates direct manipulation of the function.
- 🌟 To address absolute value functions, the limit must exist from both the positive and negative sides of the approach to zero.
- 🔄 When approaching from the positive side, x is positive, and absolute values can be removed, simplifying the expression.
- 🔄 From the negative side, the absolute value of x is considered, which affects the simplification process and the limit result.
- 📊 The process of solving these limits involves simplifying the expressions and evaluating the limits from both directions to check for consistency.
- 🚫 If the limit from the positive side does not equal the limit from the negative side, the overall limit does not exist.
- 📈 The use of a graphing calculator can provide visual confirmation of the theoretical work done to solve the limit problems.
- 🌐 For trigonometric functions like sine, the limit as x approaches 0 can often be found using known results, such as the limit of sine over x being 1.
- 🔢 Substitution is a useful technique for transforming complex expressions into simpler forms that can be more easily analyzed for limits.
- 📚 The importance of numerical approximation is highlighted as a complementary method to confirm analytical results using calculators or estimation.
Q & A
What is the mathematical concept being explored in the given script?
-The concept being explored is the calculation of limits, specifically how to deal with limits involving absolute values and how to apply substitutions to simplify and solve limit problems.
How does the script propose handling absolute values in limits?
-The script suggests removing the absolute value by considering the limit from both the positive and negative directions towards the point of interest, effectively dealing with the piecewise nature of absolute value functions.
What does the existence of a limit depend on according to the script?
-According to the script, for a limit to exist at a certain point, the limit must approach the same value from both the positive and negative directions toward that point.
What conclusion is reached for the limit as x approaches 0 of \(x - 2 \times |x|\) over \(|x|\)?
-The conclusion is that the limit does not exist, as approaching from the positive direction yields -1, while approaching from the negative direction yields -3, indicating different values from each side.
How is the limit problem involving the sine function and a coefficient inside the sine function approached?
-The problem is approached by making a substitution to simplify the expression into a form that resembles the known limit of sine of x over x as x approaches 0, which is equal to 1.
What substitution is made to simplify the limit as x approaches 0 of \( \sin(5x) / 2x \)?
-The substitution made is \(a = 5x\), which simplifies the limit problem to \( \lim_{a \to 0} \sin(a) / (2/5 a) \), allowing for easier computation.
What technique is suggested for verifying limit problems if analytical solutions are challenging?
-The script suggests a numerical approach of substituting very small numbers close to the limit point into the function and using a calculator to see what value the expression approaches, as a method of verification.
How is the limit problem of \( \sin^2(x) / x^2 \) as x approaches 0 solved?
-The problem is solved by recognizing it can be rewritten as the square of \( \sin(x) / x \), allowing the known limit of \( \sin(x) / x \) as x approaches 0, which is 1, to be applied, resulting in the final answer of 1.
What does the script imply about the graphing calculator's representation of functions?
-The script implies that while graphing calculators can confirm analytical work by showing trends as x approaches a limit, they may visually connect points in a way that oversimplifies or misrepresents the precise behavior near the limit.
What is the key message regarding the limit of \( \sin(5x) / 2x \) as x approaches 0?
-The key message is that by making an appropriate substitution and simplifying, the limit of \( \sin(5x) / 2x \) as x approaches 0 is determined to be 2.5, demonstrating how transformation techniques can simplify complex limit problems.
Outlines
📚 Solving Limit Problems with Absolute Value
The paragraph discusses the process of solving a limit problem involving the absolute value of a variable. The speaker explains the challenge of dealing with absolute values and how to approach the problem by ensuring the limit exists from both the positive and negative sides. The strategy involves simplifying the expression by removing the absolute value signs based on the sign of the variable as it approaches zero. The speaker demonstrates that the limit from the positive side is -1, while from the negative side is -3, concluding that the limit does not exist since the values from both sides are not the same. The paragraph emphasizes the importance of analytical problem-solving and the use of numerical approximations when an analytical solution is not readily available.
📈 Confirming Limit Results with Graphing Calculator
This paragraph delves into the use of a graphing calculator to confirm the results of the limit problem discussed previously. The speaker inputs the function into the calculator and zooms out to observe the behavior of the function as it approaches zero. The graphing calculator visually supports the conclusion that the limit does not exist, as the function approaches different values from the left and right sides of zero. The speaker also shares a practical tip about never getting a limit problem wrong, suggesting that if an analytical solution is not possible, one can use very small numbers close to the limit to determine the function's behavior numerically.
🌐 Understanding Limits with Substitution and Sine Functions
The paragraph focuses on solving a limit problem involving the sine function and a substitution technique. The speaker introduces a substitution where a new variable 'a' is set equal to 5x, allowing for the simplification of the original expression. By substituting and dividing both sides by 5, the speaker transforms the original limit problem into one where 'a' approaches zero, which is equivalent to 'x' approaching zero at a slower pace. The speaker then simplifies the expression by canceling out terms and applying a previously proven limit, concluding that the limit of the given function as 'x' approaches zero is 5/2. The speaker also suggests using a calculator to confirm the result with practical examples, emphasizing the importance of both analytical and numerical methods in understanding limits.
📊 Analyzing Limits with Squaring and Constant Terms
In this paragraph, the speaker tackles a limit problem involving the sine function squared and emphasizes the impact of squaring terms on the limit. The speaker explains that the presence of squared terms in the numerator and denominator does not change the fundamental approach to solving the limit problem. By treating the squared terms as constants, the speaker simplifies the expression and applies the previously established limit of sine of x over x as it approaches zero, which is 1. The speaker then squares this result to find the limit of the given function, which is 1. The paragraph highlights the importance of understanding how limit properties can be applied to more complex functions and the utility of using known limit results to solve new problems.
Mindmap
Keywords
💡limit
💡absolute value
💡approaches
💡simplify
💡substitution
💡squeeze theorem
💡graphing calculator
💡numerical approximation
💡sine function
💡exponents
Highlights
The initial problem involves a limit with an absolute value, which complicates direct manipulation.
For the limit to exist, it must hold true from both the positive and negative sides as x approaches 0.
When approaching 0 from the positive side, x is positive, allowing the removal of absolute value signs.
The limit from the positive side results in -1, by simplifying the expression to x - 2x over x, which equals -1.
When approaching from the negative side, the absolute value of x is -x, leading to a different simplification.
The limit from the negative side results in -3, showing a discrepancy from the positive side's result.
The limit does not exist as x approaches 0 due to the different values obtained from the left and right.
Graphing calculators can confirm the results of limit problems, providing a visual aid to the calculations.
The concept of limits is explored through a practical problem involving the sine function and a variable substitution.
By substituting a = 5x, the problem is transformed to resemble the known limit of sine of x over x as x approaches 0.
The limit of sine of 5x over 2x as x approaches 0 is found to be 5/2 by using the substitution method.
The problem of sine squared of x over x squared is approached by considering the squared nature of the terms.
The limit of sine squared of x over x squared is equal to the square of the limit of sine of x over x.
The constant term in the denominator allows for the simplification of the expression when considering the limit.
The final result of the limit problem involving sine squared is 1, as the base limit is 1.
The use of numerical approximation with a calculator can provide verification of limit results.
The session concludes with the presenter expressing hope that the audience found the explanations useful.
Transcripts
Browse More Related Video

Limit examples w/ brain malfunction on first prob (part 4) | Differential Calculus | Khan Academy
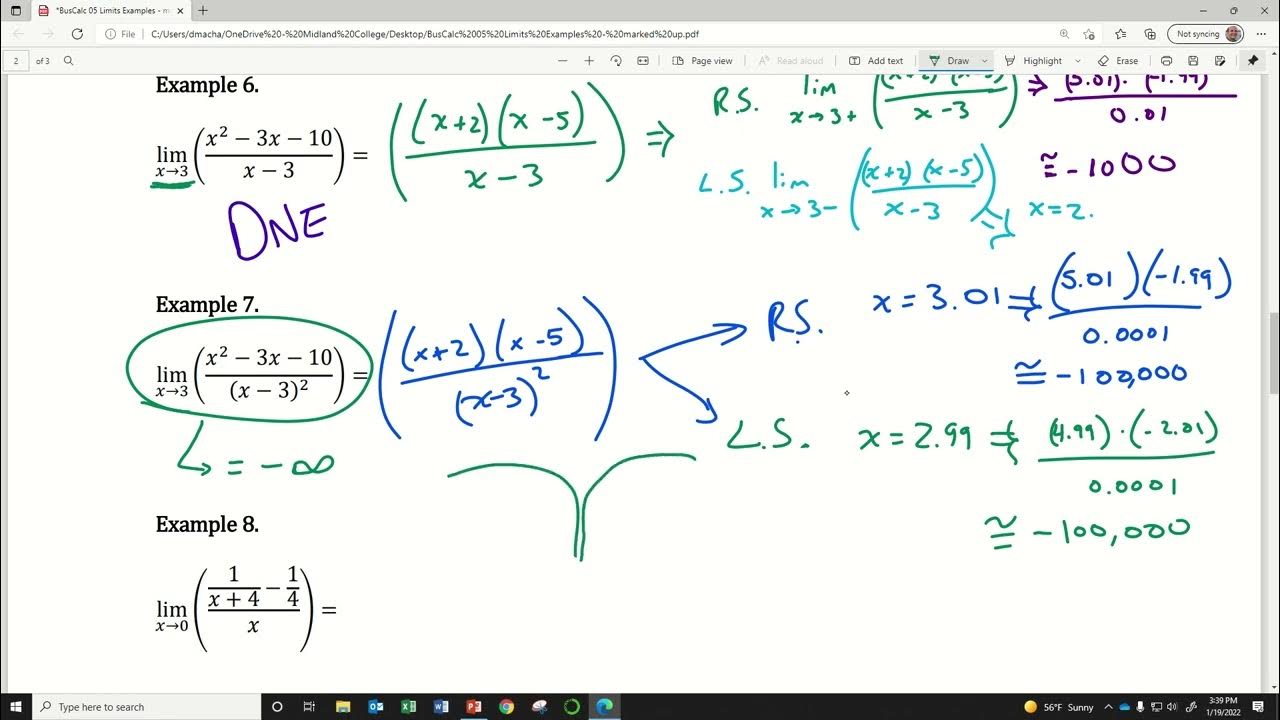
BusCalc 05 Limits Examples Pt 2

How To Evaluate Limits From a Graph
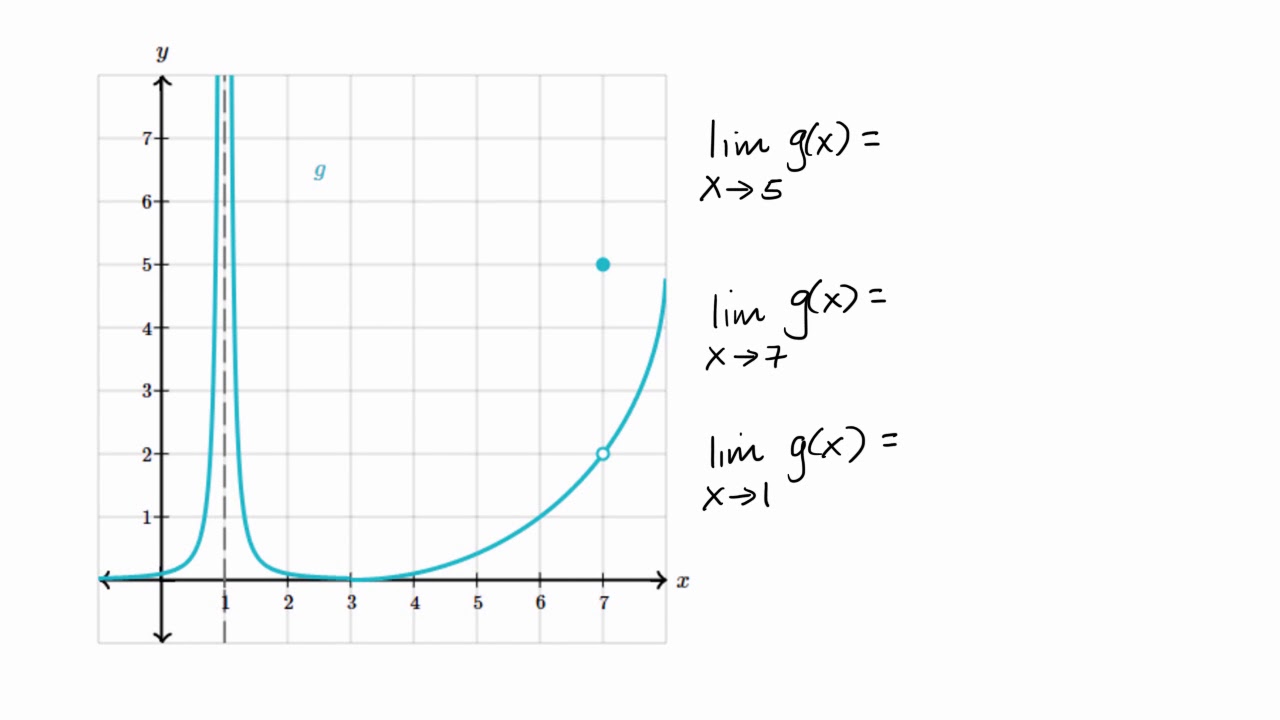
Limits from graphs | Limits and continuity | AP Calculus AB | Khan Academy

Limits at Infinity & Horizontal Asymptotes

Limits of Exponential Functions | Calculus
5.0 / 5 (0 votes)
Thanks for rating: