Limit examples w/ brain malfunction on first prob (part 4) | Differential Calculus | Khan Academy
TLDRThe video script discusses three complex limit problems from a summer calculus course, focusing on the importance of algebraic manipulation and trigonometric identities. The first problem involves factoring to solve an indeterminate form, the second requires knowledge of algebraic tricks to simplify expressions involving square roots and infinity, and the third utilizes trigonometric double angle formulas to evaluate a limit as x approaches zero. The solutions are presented in a step-by-step manner, emphasizing the process of simplifying complex expressions to find the limits.
Takeaways
- 📚 The video discusses solving limit problems in calculus, emphasizing the importance of memorizing and applying key mathematical concepts.
- 🧠 The first problem involves finding the limit as z approaches 2 of a given function, highlighting the need to factorize to solve issues with undefined values.
- 🔢 The solution to the first problem requires recognizing patterns in the numerator and denominator to factor and simplify the expression, ultimately resulting in a limit value of 1/2.
- 🌟 The second problem examines the limit as x approaches infinity of a radical expression, teaching the use of conjugates to eliminate square roots and simplify the expression.
- 📈 By dividing the numerator and denominator by the highest degree term, x, the second problem's limit is found to be 2, demonstrating the technique of reducing complex expressions.
- 📚 The third problem is a trigonometric limit as x approaches 0, showcasing the need to recall and apply trigonometric identities effectively.
- 📌 The cotangent and cosecant in the third problem are simplified using double angle formulas and basic trigonometric identities, transforming the expression into a more manageable form.
- 🤔 The challenge with the third problem lies in avoiding the undefined result when x approaches 0, which is overcome by dividing both the numerator and denominator by sine x.
- 🏆 The final answer of the third problem is 1/2, reinforcing the usefulness of trigonometric simplification and limit properties.
- 💡 The video script underscores the importance of practice and familiarity with algebra and trigonometry in tackling calculus problems, particularly those involving limits.
- 🎓 The examples provided serve as a comprehensive review for individuals preparing for more advanced calculus challenges, offering a solid foundation for tackling complex problems.
Q & A
What was the first limit problem discussed in the video?
-The first limit problem discussed was finding the limit as z approaches 2 of the function (z^2 + 2z - 8) / (z^4 - 16).
Why couldn't the first limit problem be solved by directly substituting z with 2?
-Direct substitution resulted in an undefined expression because 2^4 - 16 equals zero, which creates a division by zero situation.
How was the first limit problem solved?
-The problem was solved by factoring both the numerator and the denominator, which allowed for the cancellation of the common term (z - 2), leading to the simplified expression and the limit of 1/2 as z approaches 2.
What was the second limit problem about?
-The second limit problem was about finding the limit as x approaches infinity of the expression (sqrt(x^2 + 4x + 1) - x).
What trick was used to eliminate the square root in the second problem?
-The trick used was multiplying the expression by its conjugate, (x^2 + 4x + 1 + x), to eliminate the square root and simplify the expression.
What was the result of the second limit problem?
-The limit as x approaches infinity of the given expression was found to be 2.
What was the third limit problem discussed in the video?
-The third limit problem was finding the limit as x approaches 0 of the expression (cotangent of 2x) / (cosecant of x).
How were trigonometric identities used to simplify the third problem?
-Trigonometric identities were used to express cotangent of 2x as cosine of 2x / sine of 2x and cosecant of x as 1 / sine of x, which allowed for further simplification of the limit expression.
What was the final result of the third limit problem?
-The limit as x approaches 0 of the given expression was found to be 1/2.
What is the main takeaway from the video regarding limit problems?
-The main takeaway is that solving limit problems often involves a combination of algebraic manipulation, factoring, and the application of relevant mathematical identities to simplify the expression and make the limit easier to evaluate.
How can one prepare for similar limit problems?
-To prepare for similar limit problems, one should have a strong understanding of algebra, trigonometry, and the properties of limits, as well as practice manipulating functions to get them into a form where taking the limit is straightforward.
Outlines
📘 Limit Problems from a Calculus Course
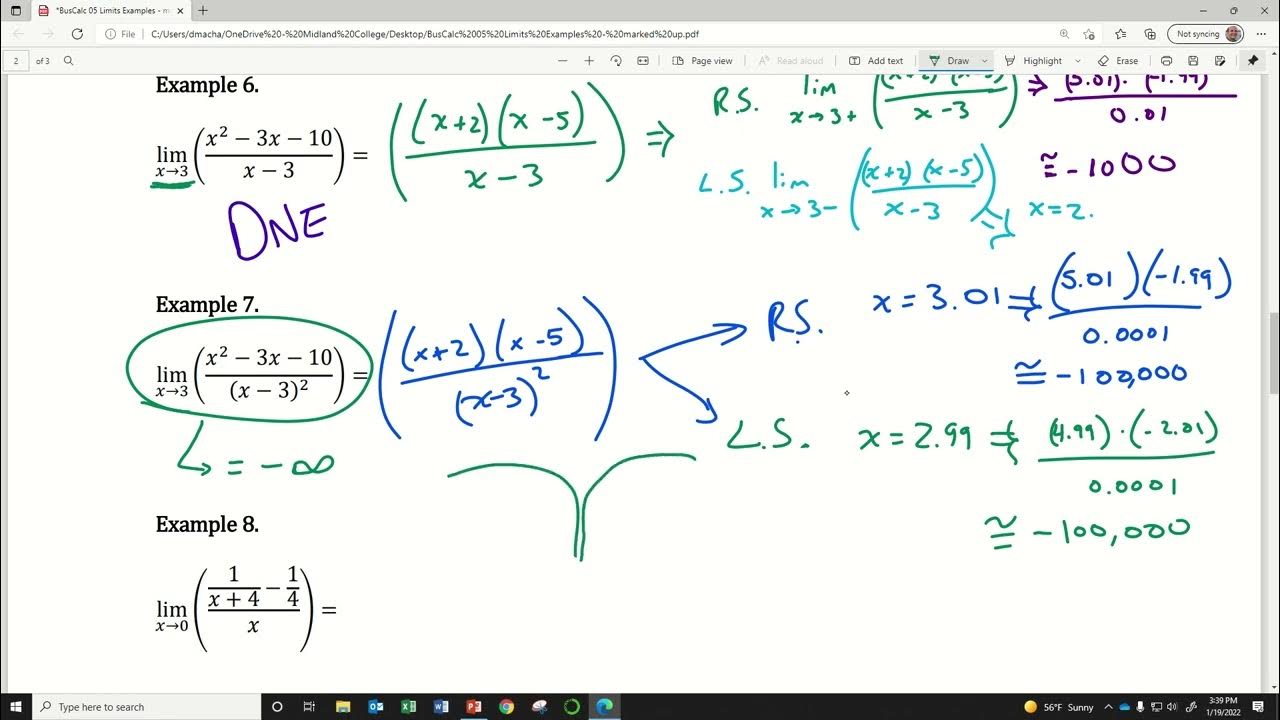
The narrator begins by sharing that his cousin Nadia, who is taking a summer calculus course, encountered some challenging limit problems. Inspired by their complexity and the process of solving them over the phone, the narrator decides to create a tutorial video. The first problem discussed involves finding the limit of a rational function as 'z' approaches 2. The solution process outlined includes an attempt to substitute the value directly, which leads to an undefined expression due to a zero in the denominator. To resolve this, factoring the numerator and denominator is suggested, revealing a common factor that, when canceled, simplifies the expression and allows for the limit to be evaluated successfully, yielding a result of 1/2. The narrator emphasizes the importance of factoring in solving limit problems where direct substitution fails due to discontinuity.
🔍 Exploring Limits with Square Roots and Conjugates
The second paragraph dives into a more complex limit problem, highlighting a common intuition trap when dealing with limits involving square roots and linear terms as the variable approaches infinity. The narrator suggests that one's initial guess might be that the expression tends toward zero, but this turns out to be incorrect. To tackle this problem, a mathematical trick involving the multiplication by the conjugate is introduced. This approach helps eliminate the square root from the equation, facilitating the simplification of the expression. Through algebraic manipulation, including dividing by the highest degree term present, the problem is simplified to a form where the limit can be readily evaluated as the variable approaches infinity, ultimately revealing the answer to be 2. This demonstrates the usefulness of conjugates in handling limits involving square roots and subtraction.
📐 Trigonometric Limits and Double Angle Formulas
In the final paragraph, the focus shifts to a trigonometric limit problem involving the cotangent and cosecant functions as the variable approaches zero. This problem illustrates the necessity of understanding and applying trigonometric identities, specifically the double angle formula, to simplify limit expressions. The narrator methodically transforms the original problem into a more manageable form by converting trigonometric functions into their reciprocals and applying identities. This simplification process reveals a discontinuity in the denominator, which is addressed by further manipulation using the double angle formula for sine. The simplification ultimately leads to a straightforward limit evaluation, with the final answer being 1/2. This example underscores the importance of algebraic manipulation and knowledge of trigonometry in solving complex limit problems.
Mindmap
Keywords
💡limit
💡factoring
💡undefined
💡continuous function
💡algebra
💡trigonometry
💡trigonometric identities
💡conjugate
💡infinite
💡simplify
Highlights
The speaker is creating videos to help their cousin Nadia with her calculus problems.
The first problem involves a limit as z approaches 2 of a given function.
The initial attempt to substitute the value into the function leads to an undefined result due to a zero in the denominator.
The solution involves factoring both the numerator and the denominator of the function.
The factored form reveals a common term in the numerator and denominator, allowing for simplification.
The limit is calculated to be 1/2 after simplification and considering the approach to the value.
The second problem involves the limit as x approaches infinity of a given radical expression.
The initial intuition about the limit is incorrect, and a specific trick is needed to simplify the expression.
The trick involves multiplying by the conjugate of the expression under the radical sign to eliminate it.
After simplification and dividing by the highest degree term, the limit approaches 2 as x approaches infinity.
The third problem is a trigonometric limit as x approaches 0.
The problem requires knowledge of trig identities to manipulate and simplify the expression.
The use of double angle formula for sine is crucial for simplifying the trigonometric expression.
The limit is found to be 1/2 after applying trigonometric identities and simplifying the expression.
The speaker emphasizes the importance of algebra and trigonometry in solving complex limit problems.
The video aims to prepare viewers for challenging problems that might be presented in a calculus course.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: