Trigonometry Basics
TLDRIn this engaging trigonometry class, the instructor simplifies the basics of trigonometry using relatable examples, such as measuring the height of Burj Khalifa. The class delves into Pythagoras theorem, defining trigonometric ratios like sine, cosine, and tangent within a right-angled triangle. The instructor also introduces standard trigonometric values for angles 0, 30, 45, 60, and 90 degrees, and their applications. The session concludes with interactive problem-solving and the importance of memorizing trigonometric tables for efficient problem-solving.
Takeaways
- 📚 The basics of trigonometry were discussed in the class, aiming to simplify the concepts for easier understanding.
- 🏗️ The class used the example of measuring the height of Burj Khalifa to introduce the practical applications of trigonometry.
- 📈 Pythagoras theorem was reviewed as a foundation for trigonometry, emphasizing the relationship between the sides of a right-angled triangle.
- 📐 Trigonometric ratios such as sine, cosine, and tangent were defined using a right-angled triangle and the angle theta.
- 🔄 Reciprocal trigonometric ratios like cotangent, secant, and cosecant were introduced as the inverses of the primary ratios.
- 📊 The relationship between sine, cosine, and tangent was highlighted, with the key formula tan(theta) = sin(theta)/cos(theta) discussed.
- 📝 The script included interactive problem-solving with the audience to find the values of trigonometric ratios for given angles and sides of a triangle.
- 🎓 The importance of memorizing standard trigonometric values for angles 0, 30, 45, 60, and 90 degrees was emphasized for quick calculations.
- 📱 The audience was encouraged to participate actively in the class and to utilize the resources available on the Manoj Academy website for further learning.
- 📅 The class also mentioned upcoming courses, including a chemistry class, and encouraged viewers to stay updated with the schedule and participate.
- 🤝 The instructor expressed gratitude for the audience's participation and engagement and encouraged continued interaction through comments and subscriptions.
Q & A
What is the main topic of the class?
-The main topic of the class is the basics of trigonometry.
What is the website mentioned for additional courses and resources?
-The website mentioned for additional courses and resources is monoshockaddme.com.
How can trigonometry be applied in real-life situations according to the class?
-Trigonometry can be applied to measure the height of tall buildings and the width of rivers without direct physical contact, as demonstrated by the examples of Burj Khalifa and a hypothetical bridge.
What is the Pythagorean theorem and how is it related to trigonometry?
-The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. It is fundamental to trigonometry as it relates the sides of a right-angled triangle, which are used to define trigonometric ratios.
What are the basic trigonometric ratios discussed in the class?
-The basic trigonometric ratios discussed are sine (sin), cosine (cos), and tangent (tan). They are defined as the ratios of the sides of a right-angled triangle: sin(θ) = opposite/hypotenuse, cos(θ) = adjacent/hypotenuse, and tan(θ) = opposite/adjacent.
What is the definition of the reciprocal trigonometric ratios secant (sec) and cotangent (cot)?
-The reciprocal trigonometric ratios are defined as the reciprocals of sine and tangent, respectively. Secant (sec) is defined as 1/cos(θ) = hypotenuse/adjacent, and cotangent (cot) is defined as 1/tan(θ) = adjacent/opposite.
What is the relationship between tan(θ) and the other trigonometric ratios?
-The relationship between tan(θ) and the other trigonometric ratios is that tan(θ) is equal to sin(θ) divided by cos(θ). This relationship is derived from the definitions of the trigonometric ratios.
How can you find the cosine of an angle if you know the tangent of that angle?
-If you know the tangent of an angle (tan(θ)), you can find the cosine of the angle (cos(θ)) by using the relationship between tangent and cosine. Specifically, cos(θ) can be found by dividing 1 by the square root of (1 + tan(θ)^2), or by using the standard trigonometric values if the angle is a known value like 30, 45, or 60 degrees.
What is the significance of the standard trigonometric values for 0, 30, 45, and 60 degrees?
-The standard trigonometric values for 0, 30, 45, and 60 degrees are important because they are the most commonly used values in trigonometry. They are easy to remember and allow for quick calculations without the need for a calculator or complex formulas. These values are also crucial for solving problems involving right-angled triangles.
What is the square relation between sine and cosine in a right-angled triangle?
-The square relation between sine and cosine in a right-angled triangle is that sine^2(θ) + cosine^2(θ) = 1. This relation holds true for any angle θ in a right-angled triangle and is derived from the Pythagorean theorem.
How can you prove the square relation sin^2(θ) + cos^2(θ) = 1?
-To prove the square relation, consider a right-angled triangle with perpendicular side length P, base side length B, and hypotenuse length H. According to the Pythagorean theorem, P^2 + B^2 = H^2. Since sin(θ) = P/H and cos(θ) = B/H, squaring both expressions and adding them together yields (P^2/H^2) + (B^2/H^2) = (P^2 + B^2)/H^2, which simplifies to 1 because P^2 + B^2 = H^2.
What is the homework question given at the end of the class?
-The homework question given is: In a right-angled triangle ABC with a 90-degree angle, where tan(C) is root 3, find the value of sine B, cos C plus cos B sine C.
Outlines
📘 Introduction to Trigonometry
The video begins with a warm welcome to a trigonometry class, emphasizing the importance of understanding the basics. The instructor introduces the concept of trigonometry by discussing its practical applications, such as measuring the height of tall buildings and the width of rivers, using the principles of trigonometry. The video also mentions the availability of detailed lectures, interactive videos, quizzes, and live classes on the instructor's website, encouraging viewers to check it out and subscribe to the YouTube channel for updates.
📗 Pythagorean Theorem and Trigonometry
The instructor delves into the Pythagorean theorem, explaining its relevance to trigonometry. Using a right-angled triangle, the theorem is described as the relationship between the squares of the triangle's sides. The video then transitions into discussing trigonometry, focusing on the right-angled triangle and the angles within it. The concept of trigonometric ratios, sine, cosine, and tangent, are introduced, explaining their relationships with the sides of the triangle and their applications in solving for unknown angles and sides.
📙 Trigonometric Ratios and Their Definitions
This section elaborates on the definitions of trigonometric ratios, including sine, cosine, and tangent, using a right-angled triangle as a reference. The instructor clarifies the meaning of each side of the triangle in the context of trigonometry and demonstrates how to calculate the ratios. The concept of reciprocal trigonometric ratios, such as cosecant, secant, and cotangent, is also introduced, providing a comprehensive understanding of how these ratios relate to one another.
📕 Relation Between Sine, Cosine, and Tangent
The instructor explores the relationship between sine, cosine, and tangent, highlighting the formula tan theta equals sine theta divided by cosine theta. The section also discusses the derivation of this relationship and its significance in trigonometry. The concept of reciprocal ratios, such as cotangent being the reciprocal of tangent, is reiterated, reinforcing the understanding of trigonometric relationships.
📔 Solving Trigonometry Problems
The video presents a practical approach to solving trigonometry problems, using given values of sine and tangent to find other trigonometric ratios. The instructor guides the viewers through the process of drawing a right-angled triangle, identifying the given values, and applying trigonometric principles to calculate the unknown sides or angles. The use of the 'K' method is introduced as a technique to handle ratios and simplify calculations.
📒 Trigonometric Values for Standard Angles
This section focuses on the standard values of trigonometric functions for specific angles—0, 30, 45, 60, and 90 degrees. The instructor provides a method to memorize these values and emphasizes their importance in solving trigonometry problems. The concept of inverting the sine values to obtain cosine values is introduced as a memory aid, and the relationship between tangent and cotangent at these standard angles is discussed.
📖 Square Relations in Trigonometry
The instructor introduces square relations in trigonometry, such as the identity sin^2(theta) + cos^2(theta) = 1, and explains their derivation and proof using the Pythagorean theorem within a right-angled triangle. The section also covers other square relations and provides techniques for proving them, encouraging students to understand and apply these relations for problem-solving.
📝 Practice Question and Homework
The video concludes with a practice question involving the calculation of trigonometric ratios for a given angle in a right-angled triangle. The instructor encourages viewers to apply the learned concepts to solve the problem and offers to review answers in the comments. Additionally, the instructor provides a homework question to further practice the application of trigonometry principles and invites viewers to participate in upcoming classes and visit the website for more resources.
🎓 Closing Remarks and Encouragement
In the closing segment, the instructor thanks the viewers for their participation and support, encourages them to like the video and subscribe to the channel, and reminds them to hit the notification bell to stay updated with the classes. The instructor also promotes the upcoming chemistry course and other offerings on the website, expressing gratitude for the engagement and participation in the trigonometry class.
Mindmap
Keywords
💡Trigonometry
💡Pythagoras Theorem
💡Trigonometric Ratios
💡Hypotenuse
💡Right-Angled Triangle
💡Sine (sin)
💡Cosine (cos)
💡Tangent (tan)
💡Applications of Trigonometry
💡Trigonometric Table
💡Manoj Academy
Highlights
Introduction to trigonometry basics in a math class format.
Discussion on how to make trigonometry easy for students.
Mention of a website for additional resources and courses.
Explanation of Pythagoras theorem and its application in trigonometry.
Definition of a right angle triangle and its components in trigonometry.
Introduction to trigonometric ratios: sine, cosine, and tangent.
Explanation of how to find the height of a building using trigonometry.
Demonstration of how to calculate the width of a river using trigonometry.
Discussion on the importance of understanding right angle triangles in trigonometry.
Explanation of the relationship between sine, cosine, and tangent ratios.
Presentation of a method to find the cosine of an angle when the tangent is known.
Introduction to standard trigonometric values for angles 0, 30, 45, 60, and 90 degrees.
Method to remember trigonometric values using a simple trick.
Explanation of the square relations in trigonometry.
Solution to a trigonometry problem using standard values and square relations.
Assignment of a homework question involving right angle triangle ABC with given tan C.
Invitation to participate in live classes and access additional courses on the website.
Discussion on the practical applications of trigonometry in measuring heights and distances.
Encouragement for students to engage with the material and ask questions.
Transcripts
Browse More Related Video
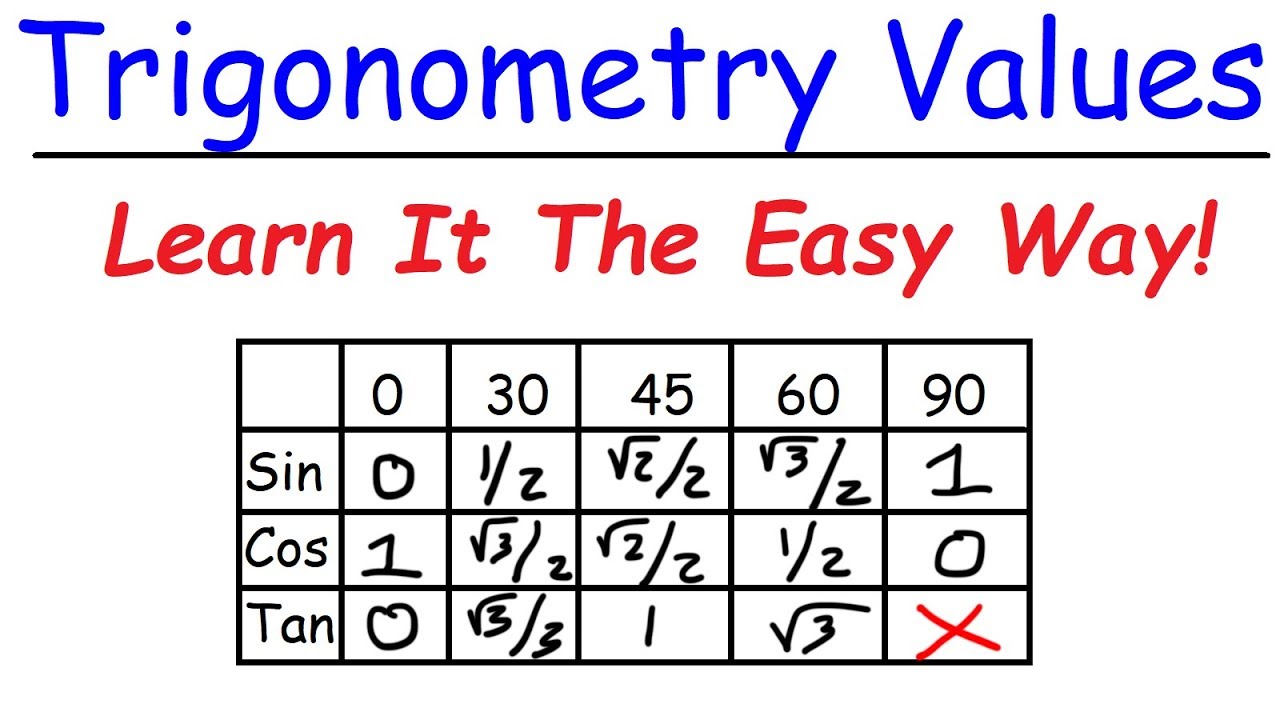
A Simple Trick To Remember Trigonometry Values

How To Find The Exact Values of Trig Functions
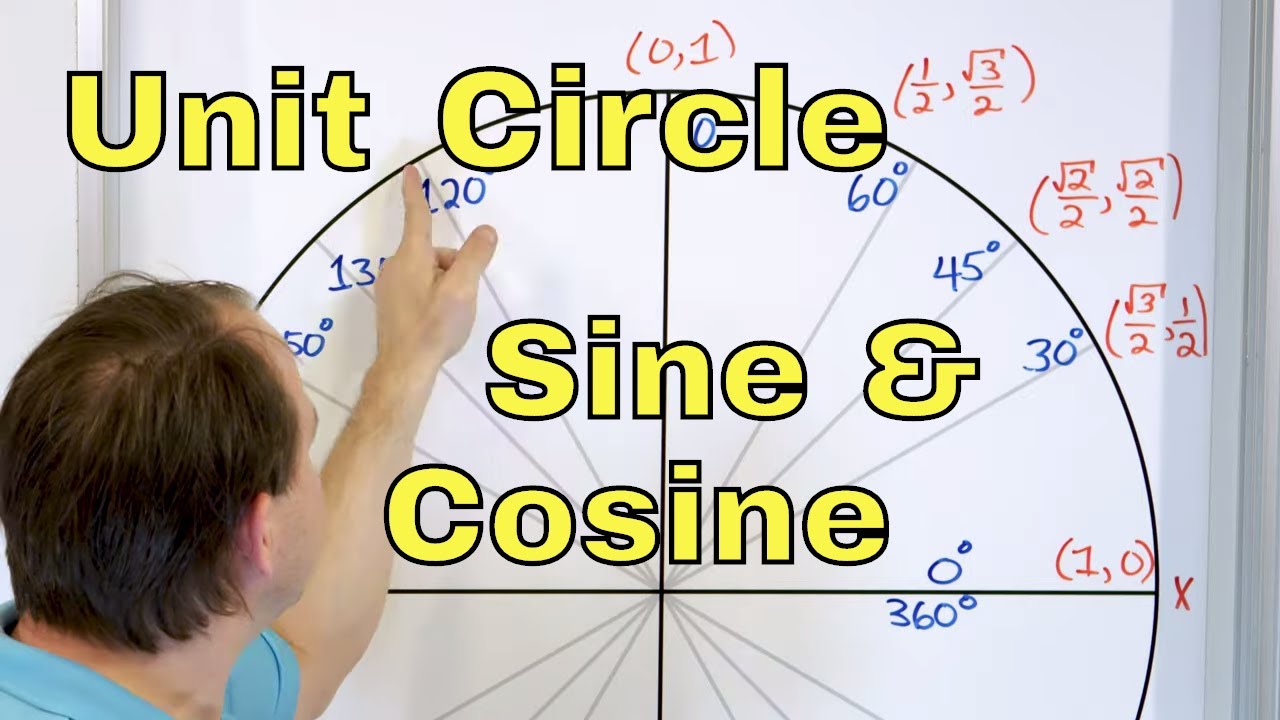
09 - Unit Circle - Definition & Meaning - Sin(x), Cos(x), Tan(x), - Sine, Cosine & Tangent

LEPT Math Majorship 2024 | Trigonometry Calculator Techniques
Trigonometric Functions: Sine, Cosine, Tangent, Cosecant, Secant, and Cotangent

30-60-90 Triangles - Special Right Triangle Trigonometry
5.0 / 5 (0 votes)
Thanks for rating: