Precalculus Introduction, Basic Overview, Graphing Parent Functions, Transformations, Domain & Range
TLDRThe video covers important precalculus topics like graphing and analyzing functions to determine their domains and ranges. It introduces basic parent functions like linear, quadratic, cubic, square root, absolute value, rational, exponential, logarithmic, trigonometric functions. It explains key features of their graphs. It then covers function transformations and how to shift/reflect graphs. It discusses function composition, inverse functions, proving functions are inverses. Overall it provides a strong base understanding of diverse function types appearing in precalculus.
Takeaways
- 😀 The domain represents the x values that a function can have, while the range represents the possible y values.
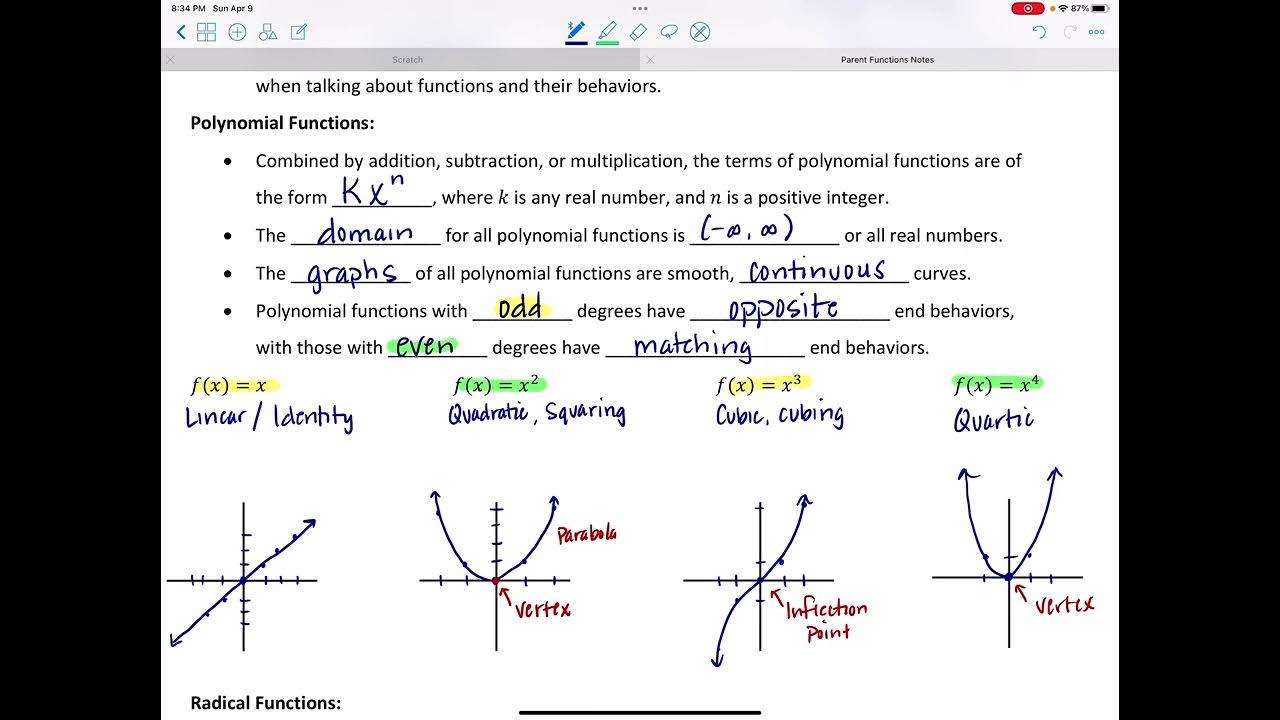
- 😎 Key parent functions include linear (y=x), quadratic (y=x^2), cubic (y=x^3), square root (y=sqrt(x)), etc.
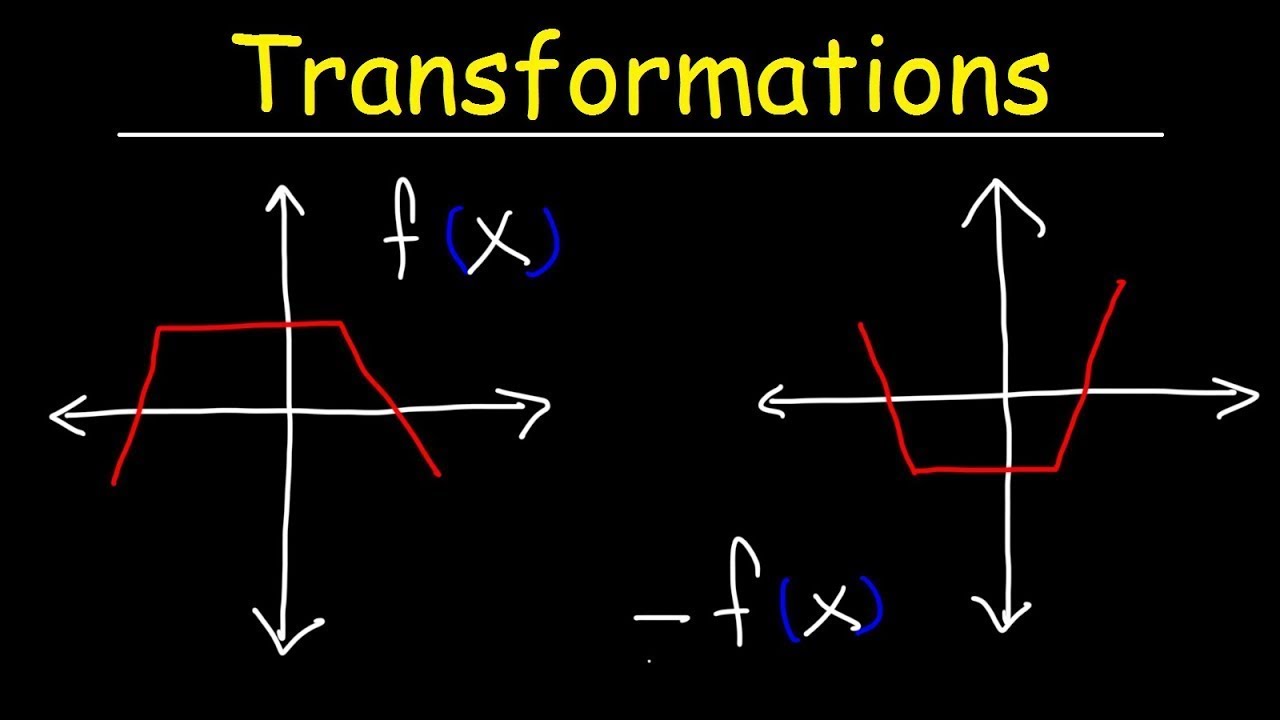
- 📈 Transformations like horizontal/vertical shifts, stretches/shrinks, and reflections over the x or y axis modify the graph of a parent function.
- 🔢 To evaluate a composite function f(g(x)), substitute g(x) into f(x) and simplify.
- ↔ To find an inverse function, swap x and y, solve for y, and verify that f(g(x))=x and g(f(x))=x.
- 🌎 The domain and range help define restrictions on the set of permissible x and y values.
- 📐 Rational functions have vertical and horizontal asymptotes that must be accounted for in the domain and range.
- 🎢 Periodic trig functions like sine, cosine and tangent repeat over a cycle and have restricted ranges.
- 📊 Exponential functions increase at an increasing rate, while logarithmic functions increase at a decreasing rate.
- ⚖️ Two inverse functions reflect symmetrically across the line y=x.
Q & A
What is a parent function in precalculus?
-A parent function is the most basic function that all other functions of that type are modeled after. Common parent functions covered in precalculus include linear, quadratic, cubic, square root, absolute value, rational, exponential, logarithmic, and trigonometric functions.
How do you determine the domain of a function?
-To find the domain of a function, look at the function from left to right. The lowest x-value it can have is the left bound of the domain, and the highest possible x-value is the right bound. Restrictions on x will narrow the domain.
What is the difference between domain and range?
-The domain represents the set of possible x-values that can be input into a function, while the range represents the set of possible y-values that the function can output.
What happens when you put a number in front of a function?
-Putting a number in front of a function, such as 2f(x), stretches the function vertically by that factor. All the y-values are multiplied by 2 in this case.
How do you find the inverse of a function?
-To find the inverse function: 1) Replace f(x) with y, 2) Switch x and y, 3) Solve for y. You must then prove f(g(x))=x and g(f(x))=x.
How can you determine if two functions are inverses of each other?
-If f(x) and g(x) are inverse functions, then f(g(x)) should equal x and g(f(x)) should also equal x. Graphically, they will be symmetrical across the line y=x.
What is a composite function?
-A composite function is formed when one function is substituted inside another function. To evaluate, insert the inner function into the outer function and simplify.
What is the domain of rational functions?
-For rational functions, the domain excludes vertical asymptotes and needs to be written in interval notation with separate sections on each side of the asymptotes.
What is the range of trigonometric functions like sine and cosine?
-Trigonometric functions repeat over every 2pi units. The range depends on the amplitude - for sin(x) and cos(x) the range is -1 to 1.
How do you graph a shifted square root function?
-Look at the sign of x and y - if they match, the graph shifts to quadrants I or III. If the signs are opposite, it shifts to quadrants II or IV. Reflect if there is a negative on the outside.
Outlines
📈 Introduction to Graphing Parent Functions and Transformations
The first paragraph introduces the key concepts that will be covered in the video, focusing on understanding different types of functions, how to graph them, determine their domain and range, and how they transform with modifications.
😀 Reviewing Linear, Quadratic, Cubic and Other Parent Functions
The second paragraph reviews the basic shapes, domains and ranges of key parent functions including linear, quadratic, cubic, square root, cube root, absolute value, rational, exponential, logarithmic and trigonometric functions.
📐 Analyzing Rational Functions and Asymptotes
The third paragraph explains more details about rational functions, how to locate their vertical and horizontal asymptotes, how transformations affect their graphing, and how to write their domain and range.
🌀 Combining Multiple Transformations and Reflections
The fourth paragraph discusses combined transformations with negatives both inside and outside a function, resulting in reflections across both the x and y-axes over the origin.
♾ Understanding Additional Function Transformations
The fifth paragraph continues explaining more examples of transformations including stretches, shrinks, and shifts for various functions.
🔁 Graphing Inverse Functions
The sixth paragraph covers inverse functions, proving functions are inverses algebraically, and showing their graphical symmetry across the line y=x.
🤝 Introducing Function Composition
The seventh paragraph introduces function composition, with examples of evaluating composite functions by nesting one function inside another.
📈 Transformations and Restrictions on Composite Functions
The eighth paragraph provides more examples working with composite functions, transformations, and restricted domains.
🔍 Finding Inverse Functions Algebraically
The ninth paragraph explains techniques for algebraically determining inverse functions, verifying functions are inverses, and graphing inverse function pairs.
🤔 Analyzing Square Root Function Transformations
The tenth paragraph works through examples of transformed square root functions, determining domains and ranges, and understanding movement to different quadrants.
😕 Defining Function Composition
The eleventh paragraph formally defines function composition, illustrates evaluation of composite functions through substitution.
✅ Verifying and Graphing Inverse Function Pairs
The twelfth paragraph shows how to algebraically prove two functions are inverses, and their graphical symmetry about the line y=x when graphed.
Mindmap
Keywords
💡function
💡domain
💡range
💡transformation
💡asymptote
💡periodic function
💡absolute value function
💡inverse function
💡exponential function
💡parent function
Highlights
Functions are used to model relationships between inputs and outputs
Key function components: domain, range, transformations, symmetries, asymptotes
Linear functions have domains and ranges from negative to positive infinity
Quadratic functions always have domain of all real numbers
Square root functions restricted by domain starting at 0
Absolute value functions always have domain of all real numbers
Exponential functions increase at an increasing rate
Log functions are inverses of exponential functions
Trig functions are periodic, with domain from negative to positive infinity
Rational functions exclude vertical asymptotes from domain
To find composite functions, substitute inner function into outer function
To find inverses, switch x and y and solve for y
Functions and their inverses reflect over the line y=x
Vertical shifts change function's horizontal asymptote
Horizontal stretches change a function's amplitude
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: