Calculus 1 Review - Basic Introduction

The Organic Chemistry Tutor

9 Jan 202126:44

EducationalLearning

32 Likes 10 Comments

TLDRThis video explains key calculus concepts like limits, discontinuities, and continuity. It starts with defining limits, explaining techniques like direct substitution and factoring to evaluate limits algebraically. It then covers graphical analysis of one-sided and two-sided limits, distinguishing between removable discontinuities, jump discontinuities, infinite discontinuities, and points of continuity. Examples illustrate evaluating limits analytically and graphically, identifying special points on graphs, and classifying the type of discontinuity represented.

Takeaways

😀 Direct substitution works to evaluate a limit if plugging in the value does not result in 0/0 or ∞/∞
😃 For limits that give 0/0 or ∞/∞, plug in values very close to the limit value instead
😉 Factor/simplify an expression first before evaluating a limit if direct substitution fails
🤓 Multiply top and bottom by a conjugate to evaluate limits with square roots
🧐 The limit exists only if the left and right hand limits match
😎 f(x) ≠ limit value indicates a removable discontinuity (hole)
🥸 Different left/right limits indicates a jump discontinuity
😳 Infinite left/right limits indicates a non-removable infinite discontinuity
🤯 All 4 values (left, right, overall limits & f(x)) match means continuity
🤠 Graphical analysis complements algebraic techniques for evaluating limits

Q & A

What is the concept of a limit and how is it used to evaluate functions?
-A limit looks at the value a function approaches as the input approaches some value. We can use limits to evaluate functions at values where direct substitution would result in an undefined or indeterminate result.
How can you evaluate a limit algebraically when direct substitution fails?
-You can factor or simplify the function, cancel out terms that would cause issues when substituted, and then evaluate the simplified function. Other techniques like multiplying by conjugates or common denominators can help simplify to allow direct substitution.
What is the difference between a left-handed and right-handed limit?
-A left-handed limit looks at the value approached as the input comes from smaller values, while a right-handed limit looks at values approached as the input comes from greater values. They allow investigating one-sided continuity.
When does a limit not exist?
-A limit does not exist if the left-handed and right-handed limits do not match. This represents a jump discontinuity in the function at that point.
How can you evaluate a limit graphically?
-Look at the function value approached from both sides along the vertical line representing the input value. If the values match, the limit exists and matches. If they differ, the limit does not exist.
What types of discontinuities can functions have?
-The main types are removable discontinuities (holes), jump discontinuities, infinite discontinuities (vertical asymptotes), and discontinuities where the function is undefined.
What does it mean for a function to be continuous?
-A function is continuous at a point if the left-hand limit, right-hand limit, two-sided limit, and function value all match at that input value.
What is a hole or removable discontinuity?
-This is when a function has a limit at a certain input but the function value there does not match. Plotting it results in a hollow point rather than solid.
What causes infinite or vertical asymptote discontinuities?
-These are caused by divisions by zero or other undefined operations in a function, causing the value to grow towards positive or negative infinity near some input.
How can you use limits to evaluate complex fractions or fractions with square roots?
-You can multiply top and bottom by a common denominator or conjugate to cancel out problematic terms before substituting the limit value.

Outlines

00:00

📉 Evaluating Limits Analytically and Graphically

This paragraph introduces the concept of limits, explaining what they represent and how to evaluate them analytically using direct substitution and algebraic techniques. It also covers how to evaluate limits graphically to understand one-sided limits and determine continuity.

05:01

🚀 Practice Problems for Evaluating Limits

This paragraph provides practice problems for evaluating limits both analytically and graphically, walking through examples factoring, using complex fractions, and applying conjugate multiplication.

10:01

📈 Using Values Close to the Limit to Check Answers

This paragraph demonstrates the technique of plugging in values progressively closer to the limit point to verify and check analytical solutions for limits.

15:02

❗ Understanding Continuity and Types of Discontinuities

This paragraph explains the connection between limits and continuity, distinguishing between removable, jump, and infinite discontinuities.

20:03

📉 More Practice with Graphical Limits and Continuity

This paragraph provides more graphical limit practice, analyzing one-sided limits to determine continuity and identify types of discontinuities.

25:07

✅ Identifying Continuity at a Point

This paragraph explains that continuity at a point occurs when the left-hand limit, right-hand limit, two-sided limit, and function value all match.

Mindmap

Keywords

💡limit

A limit describes the value that a function approaches as the input approaches some value. The video discusses techniques for evaluating limits analytically and graphically. For example, the limit as x approaches 2 of (x^2 - 4)/(x - 2) is evaluated both by direct substitution of values close to 2, and by algebraic simplification.

💡direct substitution

Direct substitution involves plugging in values close to the limit value to evaluate the function and observe the trend. It is used when plugging in the actual limit value results in an undefined or discontinuous output. For example, since f(2) is undefined for (x^2 - 4)/(x - 2), the video substitutes 1.9 and 1.99 instead.

💡continuity

Continuity refers to whether a function's graph can be drawn without lifting the pencil. The video discusses types of discontinuities like holes, infinite discontinuities, and jump discontinuities. It also shows cases where the limit equals the function value, indicating continuity.

💡removable discontinuity

A removable discontinuity is a hole in the graph at a certain point. This happens when the limit exists but does not equal the function value at that point. The video shows an example where f(-1) ?????-3, illustrating a removable discontinuity.

💡infinite discontinuity

An infinite discontinuity occurs when the function approaches positive or negative infinity from either side of a point. The video illustrates this with (x+2)/(x-2) around x = -2. The function approaches +/-??? on both sides, so there is an infinite discontinuity.

💡jump discontinuity

A jump discontinuity refers to a break or disconnect in the graph. This happens when the one-sided limits differ as the function approaches a point. For example, around x = -3, the function approaches different values from the left and right, causing a jump.

💡conjugate

The conjugate refers to changing the sign between two terms being multiplied. When simplifying a fraction with a square root term in the numerator, multiplying by the conjugate allows the terms to cancel out. The video demonstrates this with (sqrt(x - 3))/(x - 9).

💡one-sided limit

A one-sided limit looks at the function value as x approaches a point from either the left or right side. The video evaluates one-sided limits graphically around x = -3 to analyze discontinuities.

💡non-removable discontinuity

Non-removable discontinuities like infinite discontinuities and jump discontinuities cannot be resolved by defining a function value at that point. The break in the function exists inherently near that point or value.

💡hole

A hole refers to a missing point in the graph where there is a removable discontinuity. For example, around x = -1, there is a hole because even though the limit exists, f(-1) does not equal the limit.

Highlights

A limit asks what value a function approaches as the input gets arbitrarily close to some number

Direct substitution works to evaluate a limit if plugging in the target input value does not make the function undefined

Factoring or simplifying the function algebraically can allow direct substitution when it otherwise would not work

Graphically finding one-sided limits involves following the curve as x values approach the target from left or right

If left and right one-sided limits differ, the two-sided limit does not exist

When a two-sided limit exists but differs from f(x) at that point, there is a removable discontinuity

When one-sided limits differ, creating a jump, there is a non-removable discontinuity

Infinite one-sided limits signal a non-removable infinite discontinuity

Matching one-sided limits and f(x) value means the function is continuous at that point

For rational function limits, multiply numerator and denominator by a conjugate expression

Square root functions can be simplified via multiplication by the conjugate

Can check an analytic limit evaluation by graphing values close to the target x

Vertical asymptotes typically signal a function value undefined at that x

Graphical context helps interpret and visualize the meaning of limits

Understanding different types of discontinuities builds intuition for limits

Transcripts

Browse More Related Video

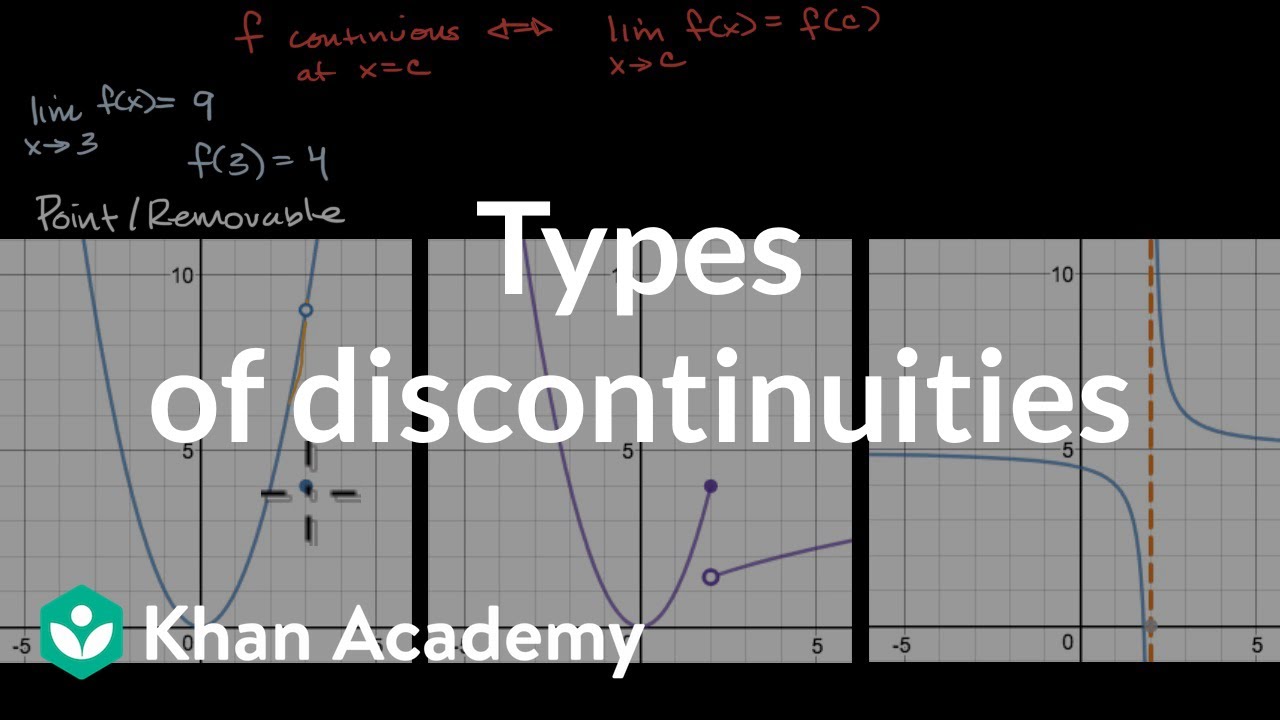
Types of discontinuities | Limits and continuity | AP Calculus AB | Khan Academy

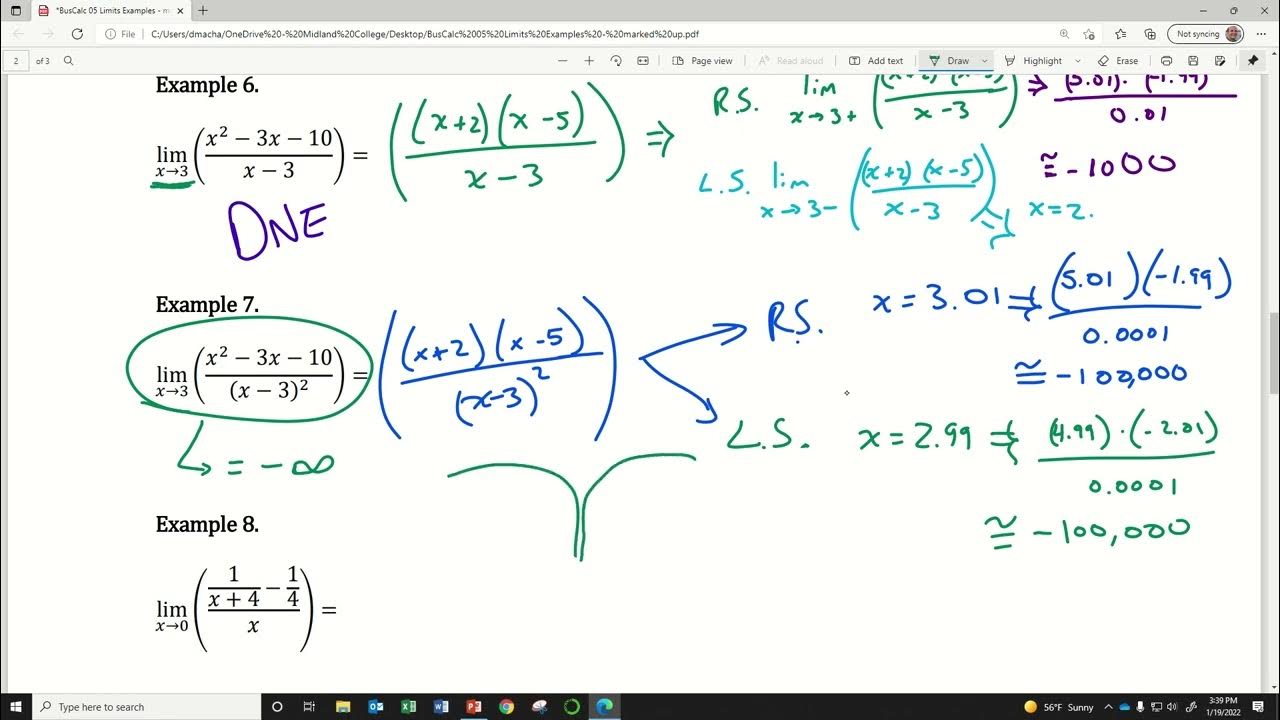
BusCalc 05 Limits Examples Pt 2

Calculus AB Homework 1.2 Understanding the Limit

AP Calculus AB and BC Unit 1 Review [Limits and Continuity]

AP Calculus AB Unit 1 Review | Limits and Continuity

Three Types of Discontinuities in Functions