Finding Sides and Angles with Right Triangle Trigonometry (Precalculus - Trigonometry 31)
TLDRThis educational video script delves into the practical application of trigonometry for solving right triangles, focusing on finding missing sides and angles. The presenter emphasizes the importance of using the Pythagorean theorem and interior angle sum theorem before resorting to trigonometric functions to avoid approximation errors. The process involves identifying the hypotenuse, labeling sides as opposite or adjacent based on the chosen angle, and then applying the appropriate trigonometric function—sine, cosine, or tangent—to find missing elements. The script also cautions against the use of rounded numbers in further calculations to prevent compounding errors. Practical examples, including calculating the height of a volcano using trigonometry, are provided to illustrate the concepts in real-world scenarios. The presenter's approachable style and step-by-step explanations make the content accessible, ensuring that viewers can grasp the fundamentals of right triangle trigonometry and apply them effectively.
Takeaways
- 📐 **Use Trigonometry Wisely**: Start with the Pythagorean theorem and interior angle sum to avoid approximations and compounding errors.
- 🔍 **Identify a Right Triangle**: Ensure the triangle is a right triangle before applying trigonometric functions.
- 🏁 **Label the Hypotenuse First**: Always label the hypotenuse before proceeding with any calculations.
- 🔢 **Find Exact Answers When Possible**: Use the Pythagorean theorem and interior angle sum to find exact values for sides and angles.
- ✅ **Complementary Angles**: In a right triangle, if one angle is known, the other can be found by subtracting from 90 degrees.
- 📉 **Avoid Rounding Errors**: Do not use rounded numbers for further calculations to prevent compounding errors.
- 🔁 **Process of Elimination**: Determine the appropriate trigonometric function by eliminating sides you don't need or can't use.
- 🔄 **Use Trigonometric Functions Correctly**: Apply the correct trigonometric function that relates the known side to the angle you're interested in.
- ↔️ **Relate Sides to Angles**: Use the tangent function when you have an angle and want to find the length of the opposite side over the adjacent side.
- 🔢 **Exact vs. Approximate Values**: When using trigonometry, calculate exact values where possible and use approximations only when necessary.
- 🚫 **Avoid Future Rounding**: Do not use approximations in subsequent calculations if you can help it, as this can introduce significant errors.
Q & A
What is the primary focus of the video?
-The video focuses on teaching how to solve for missing sides and angles in a right triangle using trigonometry, while emphasizing the importance of using the Pythagorean theorem and interior angle sum theorem when possible to avoid approximations.
Why is it important to label the hypotenuse first when working with a right triangle?
-Labeling the hypotenuse first helps in systematically identifying the opposite and adjacent sides relative to the given or known angle, which is crucial for selecting the appropriate trigonometric function to solve for the missing sides or angles.
What is the significance of using the interior angle sum theorem in a right triangle?
-The interior angle sum theorem states that the angles in a triangle add up to 180 degrees. In a right triangle, since one angle is always 90 degrees, the theorem helps easily find the other angle(s) by simple subtraction, thus providing an exact answer without the need for approximation.
Why should one avoid using approximations in trigonometric calculations?
-Using approximations can lead to rounding errors, which when compounded in further calculations, can lead to significant inaccuracies. It's better to use exact values provided by the Pythagorean theorem or interior angle sum theorem before resorting to trigonometric functions that may result in approximations.
How does the process of elimination help in selecting the correct trigonometric function?
-The process of elimination involves identifying which sides are known or needed and which are not relevant to the problem. By eliminating the sides that are not needed or are rounded, one can determine the appropriate trigonometric function (sine, cosine, or tangent) that relates the known angle to the missing sides.
What is the advantage of using the tangent function in the context of the given examples?
-The tangent function relates the angle to the ratio of the opposite side over the adjacent side. In the examples, the tangent function is chosen because it allows for the use of simpler numbers and avoids the need to use the hypotenuse, which is not given or required to be found.
How does the Pythagorean theorem provide an exact answer for the hypotenuse?
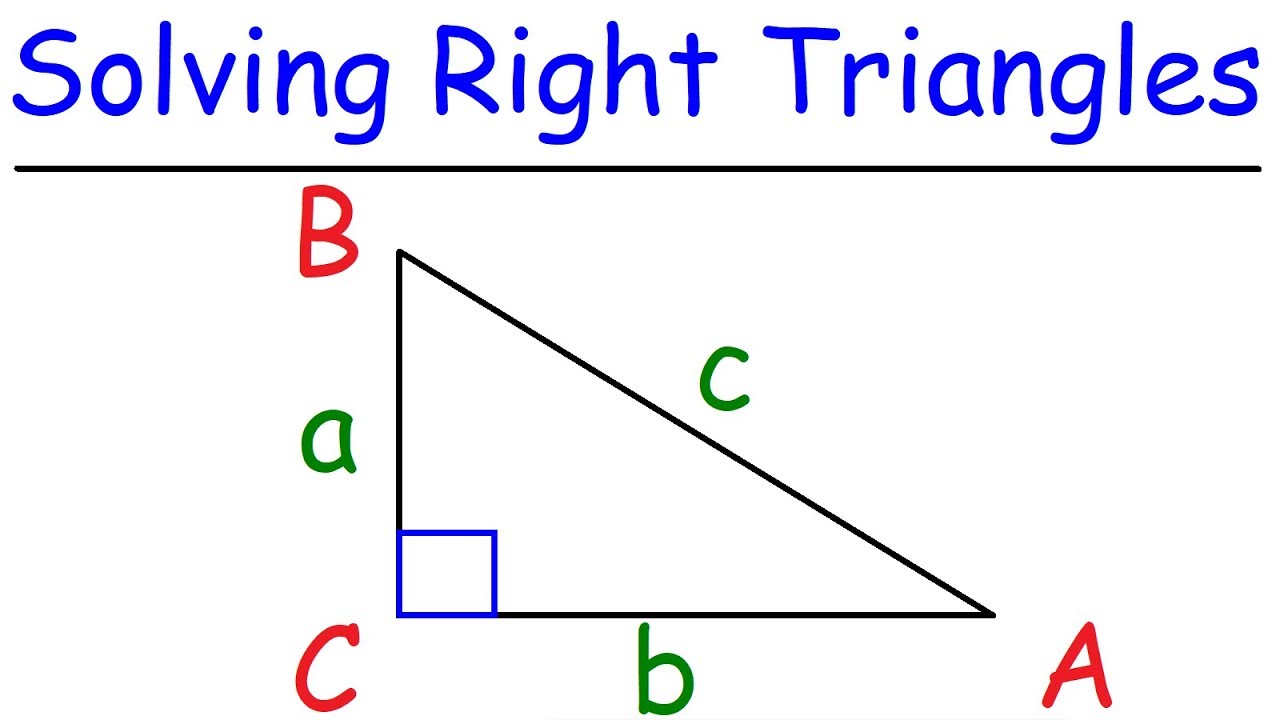
-The Pythagorean theorem states that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b), or c^2 = a^2 + b^2. By solving for c, one can find the exact length of the hypotenuse without resorting to approximations.
What is the purpose of using the sine inverse function in finding an angle measurement?
-The sine inverse function (also known as arcsine) is used to find the angle when the ratio of the opposite side to the hypotenuse (or adjacent side in the case of cosine) is known. It's the inverse operation of the sine function and provides the exact angle measurement when used with a calculator.
Why is it acceptable to use an approximation when finding the complementary angle in a right triangle?
-Subtraction is the only operation that does not compound rounding errors, so it is acceptable to use an approximation for one angle and then subtract it from 90 degrees to find the complementary angle. This is because the error from the approximation does not get compounded in the subtraction process.
How can trigonometry be applied to real-world problems, such as finding the height of a volcano?
-Trigonometry can be used to solve real-world problems by creating a right triangle where the given information allows for the calculation of missing sides or angles. For example, with an angle measurement and a known distance from the base to a certain point, the height of the volcano can be calculated using the tangent function and the given angle.
What is the final topic the video mentions that will be covered in the next lesson?
-The video concludes by mentioning that the next topic to be covered is the Law of Sines, which is used to deal with non-right triangles.
Outlines
📚 Introduction to Solving Right Triangles
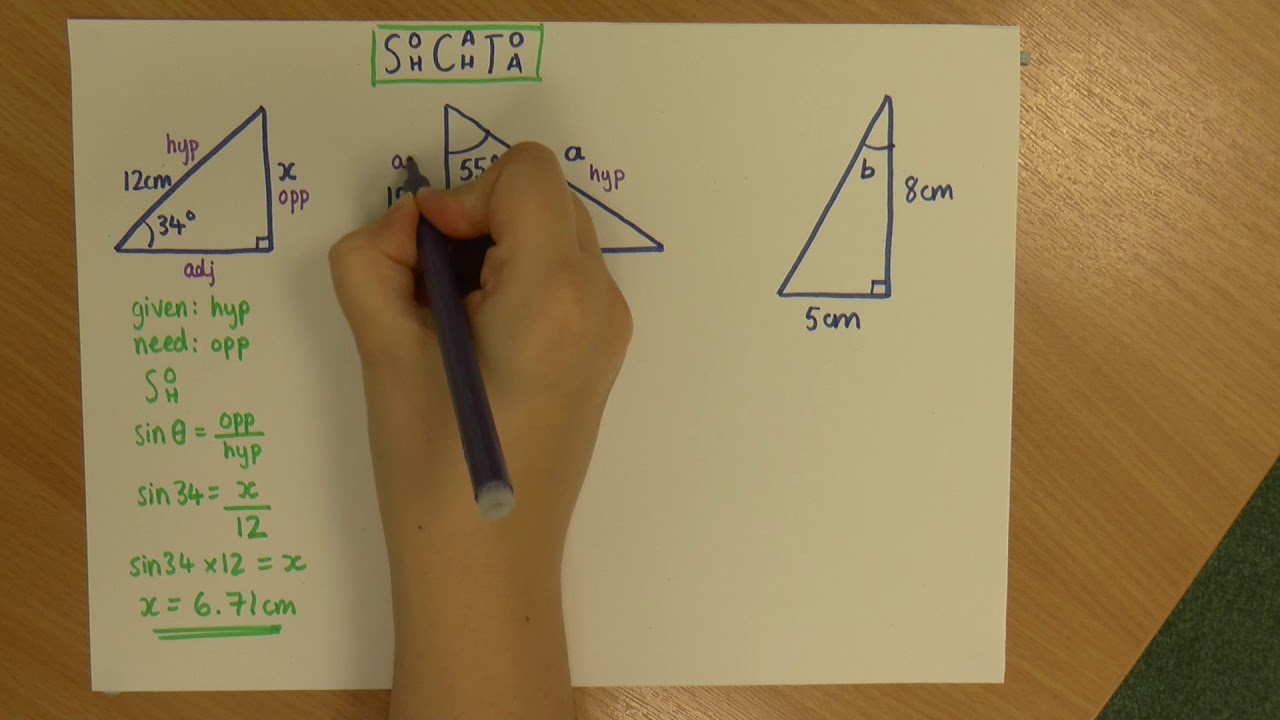
The video begins with an introduction to solving right triangles using trigonometry. The speaker emphasizes the importance of not making the problem more difficult than necessary by using the Pythagorean theorem and the interior angle sum theorem when possible. These methods provide exact answers, which are preferred over the approximations that can come from trigonometric functions. The speaker also stresses the importance of identifying the right triangle and labeling the hypotenuse first, before proceeding with trigonometric calculations.
🏗️ Right Triangle Trigonometry Setup
This paragraph focuses on the setup process for using trigonometry in right triangles. It explains the importance of labeling the hypotenuse and identifying the given or preferred angle to use in relation to the sides of the triangle. The speaker discusses the process of elimination to determine the appropriate trigonometric function to use, based on the sides that are known and the angle in question. The paragraph concludes with an example using the tangent function to find a missing side, emphasizing the importance of exact answers over approximations.
🚫 Avoiding Approximations in Calculations
The speaker cautions against using approximations in further calculations as they can compound errors. They explain that using an approximation from a trigonometric function can lead to rounding errors that, when used in subsequent calculations, can accumulate and lead to significant inaccuracies. The paragraph suggests alternative methods to find missing sides or angles without resorting to approximations, such as using the Pythagorean theorem or the properties of complementary angles in a right triangle.
🧩 Using Pythagorean Theorem and Trigonometry
The paragraph discusses the application of the Pythagorean theorem to find the hypotenuse of a right triangle when two sides are known. It highlights the preference for using the Pythagorean theorem over trigonometry to maintain exactness in measurements. The speaker then shows how to use trigonometric functions to find angles when necessary, emphasizing the process of identifying the correct sides in relation to the angle and selecting the appropriate trigonometric function to use.
🔍 Identifying Trig Functions and Exact Angles
The speaker elaborates on how to identify the correct trigonometric function to use based on the sides of the triangle that are known and the angle in question. They discuss the process of elimination to choose between sine, cosine, and tangent, and how to use the tangent inverse function to find an angle when the ratio of the opposite to the adjacent side is known. The paragraph also touches on the concept of exact answers versus approximations and the importance of using exact values in trigonometric calculations.
📐 Applications of Trigonometry in Real Life
The final paragraph presents a real-life application of trigonometry to find the height of a tall structure, such as a volcano, when direct measurement is not possible. The speaker demonstrates how to use the tangent function to relate the angle of elevation to the known distance from the base, allowing the calculation of the unknown height. This practical example illustrates the utility of trigonometric principles in solving real-world problems.
📈 Approximation and Practicality in Trigonometry
The speaker concludes with a discussion on the use of approximations in trigonometry, noting that while exact answers are preferable, approximations can be used when necessary. They provide a method for approximating the height of the volcano using a calculator and emphasize the practicality of using trigonometric functions to solve for missing sides or angles in right triangles. The paragraph ends with a teaser for the next topic, the Law of Sines, which will be used for solving non-right triangles.
Mindmap
Keywords
💡Trigonometry
💡Pythagorean Theorem
💡Interior Angle Sum
💡Hypotenuse
💡Complementary Angles
💡SOHCAHTOA
💡Exact Answer
💡Approximation
💡Error Compounding
💡Tangent
💡Inverse Trigonometric Functions
Highlights
The video teaches how to solve for missing sides and angles in a right triangle using trigonometry.
Emphasizes the importance of using the Pythagorean theorem and interior angle sum before resorting to trigonometry for exact answers.
Explains the SOHCAHTOA mnemonic for trigonometric functions in right triangles.
Details the process of identifying the hypotenuse first when working with right triangle trigonometry.
Discusses the potential for approximation errors when using trigonometric functions and the benefits of using exact values from the Pythagorean theorem.
Demonstrates how to use the tangent function to find a missing side in a right triangle.
Shows how to avoid compounding errors by not using rounded numbers in subsequent calculations.
Provides a method to find the hypotenuse using the Pythagorean theorem when two sides are known.
Explains the concept of complementary angles in a right triangle and how knowing one angle allows you to find the other.
Illustrates a step-by-step process for solving a right triangle using trigonometric functions and the elimination method.
Advises on the use of tangent inverse to find an angle when the ratio of the opposite to adjacent side is known.
Warns against the use of approximations in further math calculations to prevent cumulative errors.
Presents a real-life example of using trigonometry to find the height of a volcano when only the angle of elevation and the distance to the volcano's base are known.
Demonstrates the use of sine function to find the height of an object when the angle and the adjacent side are known.
Highlights the need to check the reasonableness of calculated results, such as the height of a volcano, with other methods or instruments.
Teaches how to use a laser rangefinder to establish a known distance and apply sine function to find the height of an object.
Concludes with a summary of the techniques for applying trigonometry to right triangles and hints at the next topic, the Law of Sines for non-right triangles.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: