Statistics Terminology and Definitions| Statistics Tutorial | MarinStatsLectures

MarinStatsLectures-R Programming & Statistics
17 Sept 201909:48
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the fundamentals of statistics, explaining its role in research across various disciplines. It outlines the process statisticians follow, from defining a research question to translating it into a statistical statement, data collection, summarization, analysis, and communication of findings. The distinction between descriptive and inferential statistics is highlighted, with examples illustrating estimation, hypothesis testing, and prediction. The script also introduces key statistical terms such as units, variables, population, sample, parameter, and statistic, emphasizing the importance of external and internal validity in ensuring the generalizability and accuracy of research findings.

Takeaways
  • 📊 Statistics is crucial in research across disciplines, requiring a stats course for data analysis.
  • 📝 Statisticians translate research questions into testable statistical statements, focusing on study design, data collection, summarization, analysis, and communication of findings.
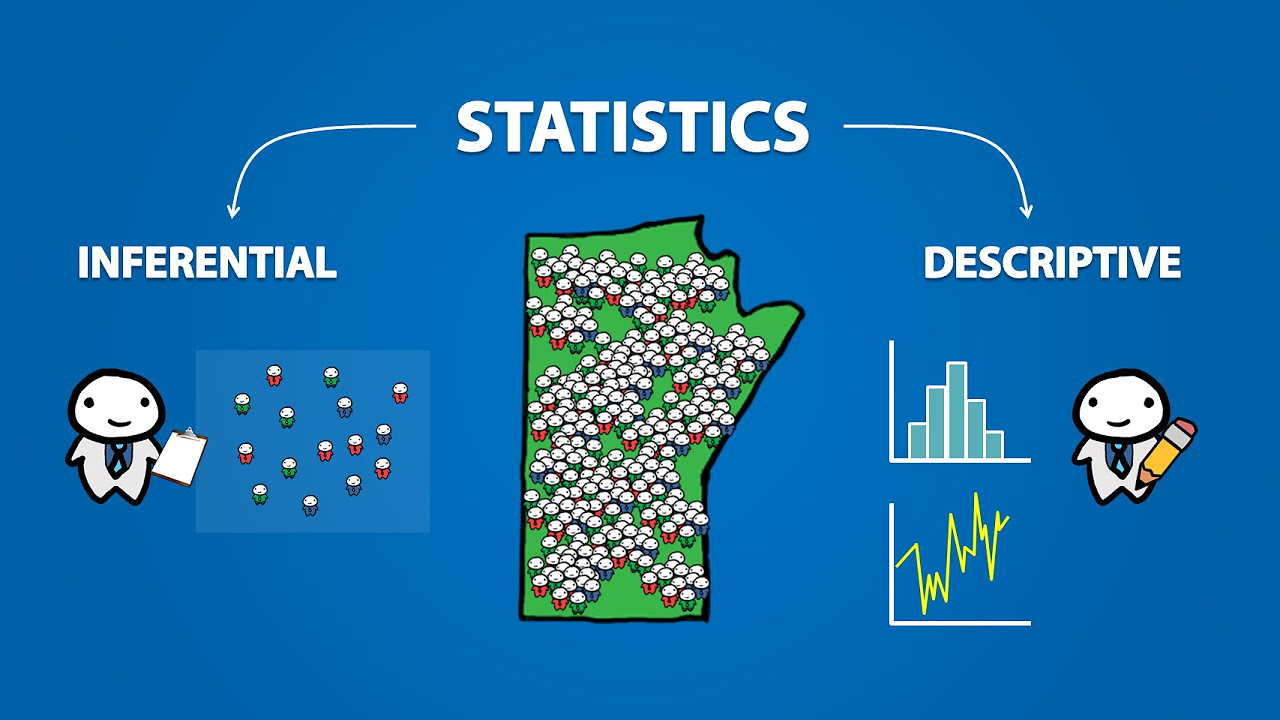
  • 💬 Statistics is divided into descriptive (summarizing data) and inferential (inferring about populations) categories.
  • 📈 Inferential statistics includes estimation, hypothesis testing, and prediction to generalize sample findings to populations.
  • 📌 Key terms include 'unit' or 'subject' for data entities, 'variable' for recorded characteristics, and 'population' versus 'sample' for study groups.
  • ✏️ Parameters and statistics differentiate between population measures and sample estimates, respectively, using specific notations (Greek for population, Latin for sample).
  • 🖥 External validity questions if sample estimates generalize to broader populations, while internal validity assesses bias and confounding within the study.
  • 🚩 A practical example in the script illustrates these concepts using a study on exercise's effect on depression among university students.
  • 👁‍🗨 The example clarifies units (students), variables (exercise, depression), population, sample, parameters, and statistics specific to the study.
  • 📄 It emphasizes the importance of considering external and internal validity in research, including potential biases and the generalizability of findings.
Q & A

  • What is the primary purpose of statistics in research?

    -The primary purpose of statistics in research is to define a research question and translate it into a statistical statement that can be tested using data. It helps in designing the study, collecting data, summarizing it, analyzing, and generalizing the findings back to the population of interest.

  • What are the two main categories of statistics?

    -The two main categories of statistics are descriptive and inferential. Descriptive statistics involve summarizing and describing data, while inferential statistics use sample data to make inferences about a population.

  • What is the difference between a parameter and a statistic?

    -A parameter is a characteristic or measure of a population, while a statistic is the estimate of that parameter based on a sample. For example, the population mean (parameter) is estimated by the sample mean (statistic).

  • Why is it important to consider external validity in a study?

    -External validity is important because it determines how well the results of a study can be generalized to an external population. If the sample is not representative of the population, the findings may not apply to others outside the sample.

  • What factors can affect the internal validity of a study?

    -Internal validity can be affected by biases or confounding variables that were not controlled for in the study. Factors such as biological sex, major subject of study, or other individual characteristics can influence the outcomes and question the accuracy of the sample estimate.

  • How does the concept of a sample relate to a population in statistical research?

    -A sample is a subset of the population that is used to represent and study the entire population. The goal is to ensure that the sample is representative of the population so that the findings can be generalized back to the population of interest.

  • What are some common descriptive statistics used to summarize data?

    -Common descriptive statistics include measures such as the mean, median, standard deviation, and various types of plots or graphs that help visualize the data.

  • What is the role of hypothesis testing in inferential statistics?

    -Hypothesis testing is used in inferential statistics to determine if there is enough evidence in the sample data to infer that a certain condition holds true for the entire population. It often involves formulating a null hypothesis and an alternative hypothesis and then testing these using the sample data.

  • What is the difference between estimation and prediction in statistics?

    -Estimation in statistics involves using sample data to estimate a parameter of the population, such as the average salary of CEOs. Prediction, on the other hand, uses a statistical model to forecast outcomes for individual cases, such as estimating a specific CEO's salary based on the model.

  • How do researchers ensure that their findings are generalizable?

    -Researchers ensure generalizability by using representative sampling methods, controlling for confounding variables, and ensuring that the study design and sample size are appropriate for the population of interest.

  • What is the significance of the difference between Greek and Latin letters in statistical notation?

    -In statistical notation, Greek letters are typically used to represent population or true values, while Latin letters represent sample estimates. This distinction helps differentiate between the actual population parameters and their estimated values derived from samples.

Outlines
00:00
📊 Introduction to Statistics and Terminology

This paragraph introduces the concept of statistics as the foundation of most research, regardless of discipline. It outlines the role of statisticians in defining research questions, designing studies, collecting and summarizing data, analyzing findings, and communicating results. The distinction between descriptive and inferential statistics is explained, with descriptive focusing on data summarization and inferential aiming to generalize from a sample to a population. The paragraph also introduces the concepts of estimation, hypothesis testing, and prediction within inferential statistics.

05:01
🔍 Understanding Research Design and Data

The second paragraph delves into the specifics of research design and data analysis. It discusses the importance of external and internal validity in research. External validity questions the generalizability of sample estimates to an external population, while internal validity assesses whether the sample estimate is unbiased. The paragraph uses the example of a study on depression rates among university students and regular exercise to illustrate these concepts. It highlights the need to consider factors like geography and majors that might affect depression rates and exercise habits, emphasizing the importance of controlling for these variables to ensure the study's internal validity.

Mindmap
Keywords
💡Statistics
Statistics is the science of analyzing and interpreting data. It serves as the foundation for most research across various disciplines, both within and outside academia. In the context of the video, statistics is used to define a research question, collect and summarize data, and make inferences about a population based on that data.
💡Descriptive and Inferential Statistics
Descriptive statistics involve summarizing and describing the main features of a dataset, often using graphs or numerical measures like mean, median, and standard deviation. Inferential statistics, on the other hand, use sample data to make inferences about a larger population. This includes estimation, hypothesis testing, and prediction.
💡Unit or Subject
A unit or subject refers to the individual entities or people on which data is collected. In statistical research, understanding the units helps in designing the study and collecting relevant data for analysis.
💡Variable
A variable is a characteristic or attribute of a unit that varies across the units and can be measured or observed. In a dataset, variables are typically organized in columns, with each row representing a unit.
💡Population
The population in statistics refers to the entire group of individuals or units that a study is interested in examining. It is the target to which the research findings are meant to be generalized.
💡Sample
A sample is a subset of the population selected for study. It is used to represent the population in statistical analysis due to practical reasons, as studying an entire population can be impractical or impossible.
💡Parameter and Statistic
A parameter is a numerical characteristic of a population, while a statistic is the corresponding estimate derived from a sample. Parameters are what we aim to estimate or understand, and statistics are our best guesses about those parameters based on sample data.
💡External Validity
External validity concerns the extent to which the results of a study can be generalized to other populations or situations beyond the sample studied. It asks whether the findings are applicable to different contexts.
💡Internal Validity
Internal validity refers to the accuracy and credibility of a study's findings. It involves assessing whether the sample estimate is unbiased and whether there are any confounding factors that could affect the results.
💡Estimation
Estimation in statistics is the process of determining a likely value or range for a population parameter based on sample data. It involves making educated guesses about the population from the information derived from a sample.
💡Hypothesis Testing
Hypothesis testing is a statistical method used to make decisions about the population based on sample data. It involves formulating a null hypothesis and an alternative hypothesis, and then using statistical tests to determine if there is enough evidence to reject the null hypothesis.
💡Prediction
Prediction in statistics involves using a statistical model to forecast outcomes or future values for individual cases based on the relationships found in the data.
Highlights

Statistics serves as the backbone of most research, both within and outside of academia.

Statisticians define a research question and translate it into a statistical statement using data.

Descriptive and inferential statistics are the two main categories, with descriptive focusing on summarizing data and inferential on making generalizations about a population.

Inferential statistics involve estimation, hypothesis testing, and prediction to understand population characteristics based on sample data.

Vocabulary such as units, subjects, variables, population, and sample are essential for understanding statistical concepts.

A population is the group of interest for a study, often too large or impractical to study entirely, leading to the use of samples.

Parameters are quantities of interest for the entire population, while statistics are sample-based estimates of these parameters.

External validity questions whether the sample estimate can be generalized to an external population.

Internal validity assesses whether the sample estimate is unbiased and free from confounding factors within the study.

An example study explores whether regular exercise decreases the risk of depression among university students.

The unit of observation in the study is the university student, with variables being exercise habits and depression status.

The population of interest is the general population of university students, with the sample being 5000 students from a particular university.

The parameter of interest is the true difference in depression rates between those who exercise regularly and those who don't.

The sample statistic is the observed difference in depression rates between exercising and non-exercising students within the sample.

External validity concerns arise when the sample's generalizability to the broader population is questioned due to potential differences.

Internal validity is threatened by uncontrolled factors such as biological sex and major of study that could influence depression rates.

The study aims to build and expand on these foundational concepts to deepen understanding of statistical analysis.

Transcripts

Browse More Related Video

Elementary Stats Lesson #1

Descriptive vs Inferential Statistics

Quantitative Data Analysis 101 Tutorial: Descriptive vs Inferential Statistics (With Examples)

Tutorial 1- What Is Statistics And What Are Its Types In Hindi?

Introduction to Statistics (1.1)

Statistics Lecture 4.2: Introduction to Probability

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistics101DataAnalysisInferentialMethodsDescriptiveStatsResearchToolsEducationalContentScientificStudyDataVisualizationStatisticalInferenceResearchCommunication