Tensors for Beginners 15: Tensor Product Spaces
TLDRThis video script delves into the formal definition of the tensor product, a fundamental concept in mathematics and physics, and introduces tensor product spaces. It explains how tensors, when combined, can form linear maps and bilinear forms, and how they follow specific scaling and addition rules. The script clarifies the distinction between the 'little' tensor product of individual tensors and the 'big' tensor product of vector spaces. It also highlights the role of tensors as multilinear maps, emphasizing their linearity in each input variable while all other inputs are held constant, showcasing the versatility of tensors in various mathematical operations.
Takeaways
- 📚 The video script provides a formal definition of the tensor product, which is a fundamental concept in understanding how tensors combine and interact in mathematics and physics.
- 🔍 The speaker introduces tensor product spaces, which are new vector spaces formed by the combination of existing vector spaces using the tensor product.
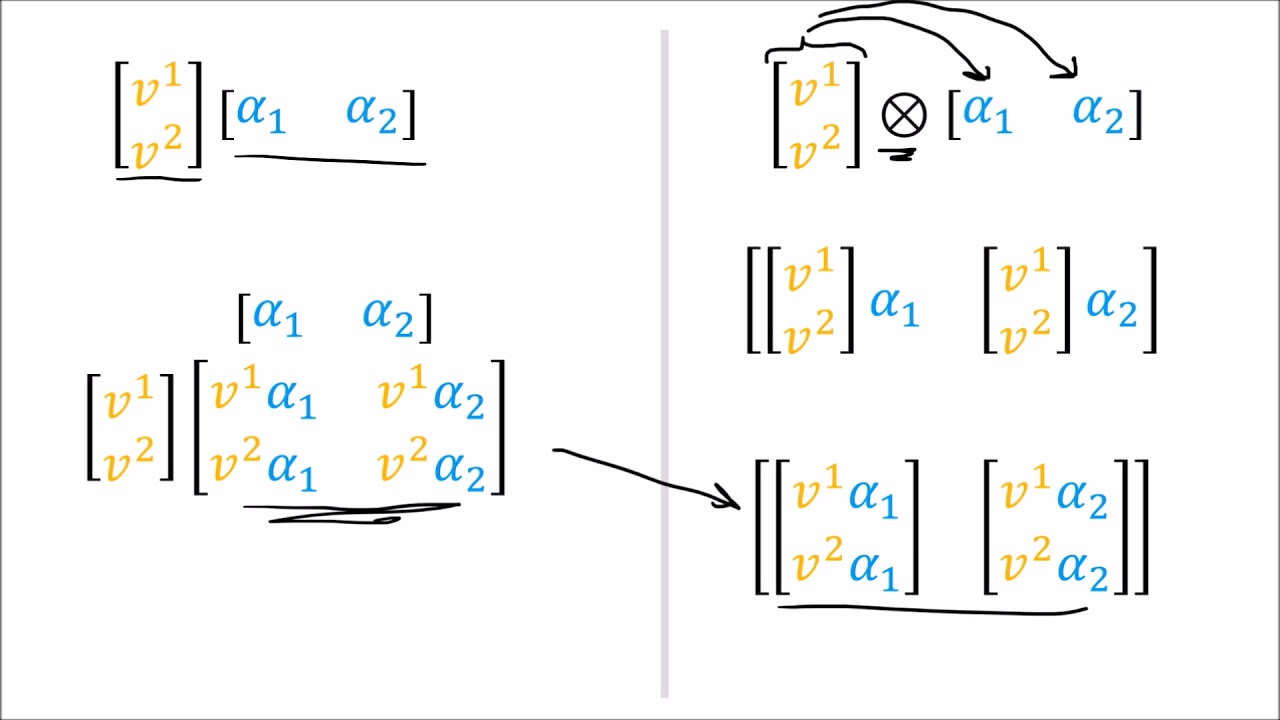
- 📌 The script clarifies that the tensor product can be represented using non-standard notation, omitting the circle times symbol typically used in textbooks.
- 🔢 The concept of combining vectors and covectors using the tensor product to create linear maps and bilinear forms is explained, emphasizing the role of the Kronecker product in this process.
- ⚖️ Scaling rules for tensor products are discussed, illustrating that scaling an entire collection of tensors can be equivalent to scaling any individual tensor within that collection.
- 🔄 The addition rules for tensor products are outlined, showing how common factors can be factored out when dealing with sums of tensor products.
- 📐 The script explains how the tensor product can combine two arrays, two tensors, or two vector spaces, highlighting three different uses of the tensor product.
- 🌐 The elements of the new vector space formed by the tensor product of a vector space and its dual (V-tensor-V*) are described, including their role as (1,1)-tensors.
- 🔑 The script explores how tensors can act as multilinear maps, emphasizing their linearity in each input variable when all other inputs are held constant.
- 🧠 The importance of understanding the tensor product for grasping the behavior of tensors in various mathematical and physical contexts is emphasized.
- 📈 The video concludes by reinforcing the idea that tensors, as multilinear maps, follow specific properties that make them versatile tools in higher-dimensional mathematics.
Q & A
What is the purpose of formally defining the tensor product in this video?
-The purpose is to provide a clear understanding of the tensor product and its properties, including how it combines tensors and forms new vector spaces, and to introduce the concept of tensor product spaces.
Why does the video mention non-standard notation for the tensor product?
-The video mentions non-standard notation to clarify that the presenter is using a different representation than the traditional circle time symbol found in textbooks, which might help in understanding the concept more intuitively.
How does the tensor product combine a vector and a covector to create a linear map?
-The tensor product combines a vector and a covector by using their Kronecker product, which results in an array whose entries represent the linear map's coefficients.
What is a Kronecker product and how is it related to the tensor product?
-The Kronecker product is an operation that takes two arrays and creates a new array by multiplying the elements of one array by the other. It is related to the tensor product as it represents the coefficients of the linear map formed by the tensor product of a vector and a covector.
What are the scaling and adding rules for the tensor product?
-The scaling rule states that scaling the entire collection of tensors by a number 'n' is equivalent to scaling any single tensor within the product. The adding rule allows for factoring out common tensors on either side of a sum of tensor products.
How do the scaling and adding rules relate to the concept of a vector space?
-The ability to scale and add tensors according to specific rules indicates that these tensors form a vector space, where operations such as scalar multiplication and vector addition are well-defined.
What is the significance of the tensor product of vector spaces, and how is it denoted?
-The tensor product of vector spaces combines two vector spaces into a new vector space, which contains tensors that follow the scaling and adding rules. It is denoted using the tensor product symbol, such as V-tensor-V*.
What are the different types of tensors that can be formed using the tensor product of vector spaces?
-Different types of tensors include (1,1)-tensors, which are vector-covector pairs and their linear combinations, and (0,2)-tensors, which are covector-covector pairs and their linear combinations.
How can the elements of the vector space V-tensor-V* be interpreted in terms of functions?
-The elements of V-tensor-V* can be interpreted as multilinear maps that take vectors and covectors as inputs and can output vectors, covectors, or scalars, depending on the specific tensor and the number of summations performed.
What is the definition of a multilinear map, and why are tensors considered multilinear maps?
-A multilinear map is a function that is linear in each input variable while all other inputs are held constant. Tensors are considered multilinear maps because they obey the properties of linearity in each input when all other inputs are fixed.
How do the components of tensors from different vector spaces determine their behavior as functions?
-The components of tensors, which have specific combinations of upstairs and downstairs indexes, determine how they behave as functions. For example, tensors with upper indexes imply vector components, while those with lower indexes imply covector components, affecting the type of output they produce when acting on other tensors.
Outlines
📚 Introduction to Tensor Product Definition
This paragraph introduces the formal definition of the tensor product, a concept previously discussed in a more informal manner. The speaker clarifies that they will be using a non-standard notation, omitting the circle time symbol typically used in textbooks. The explanation begins with the tensor product's role in creating linear maps from the combination of vectors and covectors, highlighting the relationship between the tensor product and the Kronecker product. The paragraph establishes the foundational rules for scaling and addition within the context of tensor products, emphasizing their equivalence to array multiplication and the ability to factor common elements in both operations.
🔍 Exploring Tensor Product Spaces and Their Elements
The second paragraph delves into the concept of tensor product spaces, illustrating how they are formed by combining vector spaces, specifically V and V*, and denoted using a modified circle time symbol. The speaker distinguishes between the 'little' tensor product of individual tensors and the 'big' tensor product of entire vector spaces. The paragraph also discusses the nature of elements within the newly formed vector space V-tensor-V*, describing them as vector-covector pairs and their linear combinations. The potential actions of these elements as linear maps, bilinear forms, or functions to scalars are explored, demonstrating the versatility of tensors as (1,1)-tensors within the vector space.
🌐 Understanding Higher Order Tensor Products and Multilinearity
This paragraph extends the discussion to higher order tensor products, such as the combination of two covectors within the vector space V*-tensor-V*, resulting in (0,2)-tensors. The speaker explains how these tensors can act as bilinear forms or maps from vectors to covectors, depending on the summation performed over their indices. The paragraph further illustrates how tensors can be constructed with various combinations of upstairs and downstairs indexes, reflecting their origin from either V or V*. The concept of multilinear maps is introduced, emphasizing that tensors, when used as functions, are linear in each input variable while all other inputs are held constant, a property inherent to all tensors.
📘 Conclusion on Tensors as Multilinear Maps
The final paragraph summarizes the key takeaways from the video: the formal definition of the tensor product, the creation of new vector spaces through the tensor product of existing ones, and the identification of tensors as multilinear maps. It reiterates that tensors, by their nature, adhere to the principles of scaling and addition, and that their behavior as functions is characterized by linearity in each input variable, solidifying the understanding of tensors as fundamental objects in the study of vector spaces and linear algebra.
Mindmap
Keywords
💡Tensor Product
💡Kronecker Product
💡Bilinear Form
💡Vector Space
💡Covector
💡Linear Map
💡Multilinear Map
💡Upstairs and Downstairs Index
💡(1,1)-Tensor
💡(0,2)-Tensor
Highlights
Introduction to formally defining the tensor product and its behavior.
Use of non-standard notation for the tensor product, opting to omit the circle time symbol.
Explanation of how the tensor product combines a vector and a covector to form a linear map.
Demonstration of the Kronecker product's role in representing the coefficients of the linear map.
Discussion on combining two covectors using the tensor product to create a bilinear form.
Introduction of the tensor product operation starting with array multiplication.
Scaling rules for tensor products and their equivalence to array multiplication.
Addition rules for tensor products and their simplification when sharing common terms.
Illustration of how tensor products cannot be simplified when terms have nothing in common.
Introduction of vector space concepts in relation to tensor products.
Identification of the vector space 'V-tensor-V*' as the space for vector-covector pairs.
Differentiation between the 'little' tensor product of individual tensors and the 'big' tensor product of vector spaces.
Description of the elements within the vector space V-tensor-V* as (1,1)-tensors.
Explanation of how tensors can act as multilinear maps with respect to their inputs.
Introduction of the concept of (0,2)-tensors within the vector space V*-tensor-V*.
Discussion on the construction of larger vector spaces using the tensor product and their respective components.
Clarification on how to determine the correct component indexes for new tensors from unfamiliar vector spaces.
Final summary of the video's main points: tensor product definition, formation of new vector spaces, and the multilinearity of tensors.
Transcripts
Browse More Related Video

Tensors for Beginners 10: Bilinear Forms

Tensor Operations: Contractions, Inner Products, Outer Products

Tensors for Beginners 14: Tensors are general vector/covector combinations

Video 20 - Tensor Algebra

Tensor space theory I: over a field - Lec 08 - Frederic P Schuller
Tensors for Beginners 12: Bilinear Forms are Covector-Covector pairs
5.0 / 5 (0 votes)
Thanks for rating: