Tensor space theory I: over a field - Lec 08 - Frederic P Schuller
TLDRThe provided transcript is an in-depth exploration of vector spaces, fields, rings, and linear maps within the context of abstract algebra and linear algebra. It begins with an introduction to vector spaces, emphasizing the importance of an underlying field and the structure it provides. The lecturer then contrasts fields with rings, highlighting the absence of multiplicative inverses in the latter. The concept of modules over a ring is introduced as a generalization of vector spaces. The discussion moves on to linear maps, or homomorphisms, and their role in preserving structure, leading to the definition of isomorphisms and the isomorphism theorem. The text also touches on tensor products and their significance in creating new tensors from existing ones. The dual space of a vector space and its relationship to the original space, particularly in the context of finite-dimensional spaces, is also covered. The lecturer concludes with a discussion on the transformation rules for components of vectors, co-vectors, and tensors under a change of basis, and the determinant as a key concept in linear algebra, applicable to endomorphisms and bilinear forms, with a caution against misapplying determinant calculations to inappropriate structures. The summary underscores the importance of understanding these mathematical structures and operations in a rigorous, basis-free manner.
Takeaways
- 📚 A vector space is an algebraic structure built on a field, which is a set with two operations satisfying certain properties.
- 🔍 A field is a set equipped with two operations (addition and multiplication) that are commutative, associative, and have identity elements and inverses.
- 🔢 A ring is a weaker algebraic structure than a field, with two operations that satisfy commutativity and associativity for addition but not necessarily for multiplication.
- 📈 Vector spaces can be defined over a field, and the operations within a vector space are distinct from the operations of the underlying field.
- 🔗 Linear maps, also known as homomorphisms, preserve the structure of vector spaces and are essential for understanding the relationship between different vector spaces.
- ⚙️ An isomorphism is a bijective linear map that reflects the structure of the vector spaces involved, indicating they are essentially the same.
- 🔬 The dual vector space, denoted V*, consists of linear functionals that map vectors to scalars and is important for studying the properties of a vector space.
- 🤖 The tensor product, denoted T, is a way to construct new tensors from existing ones and is fundamental in multilinear algebra.
- 📊 The dimension of a vector space is the number of elements in a basis and can be finite or infinite, affecting the properties and operations of the space.
- 🧩 A basis is a set of vectors that are linearly independent and span the entire vector space, providing a framework for expressing any vector in the space.
- 🔀 The change of basis is a process that allows us to understand how components of vectors and tensors change when switching between different bases in a vector space.
Q & A
What is a vector space built upon?
-A vector space is built upon a structure known as a field, which is an algebraic field in the context of mathematics. This field consists of a set K with two operations, plus and times, satisfying certain properties like commutativity, associativity, and the existence of neutral and inverse elements.
What is the difference between a field and a ring in algebraic structures?
-A field is an algebraic structure where the set K with two operations, plus and times, satisfies a set of axioms including commutativity, associativity, the existence of neutral and inverse elements for addition, and multiplication. A ring, on the other hand, is a weaker structure that only requires the set to be an abelian group under addition and does not necessitate the existence of multiplicative inverses or commutativity of multiplication.
How are vector spaces and fields related?
-A vector space is defined over a field. The operations of the vector space (addition and scalar multiplication) are distinct from those of the underlying field. The field provides the scalars used to create vectors in the vector space through scalar multiplication.
What is a linear map?
-A linear map is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. It is a structure-preserving map that satisfies the properties of additivity and homogeneity.
What is a vector subspace?
-A vector subspace, or simply subspace, is a subset of a vector space that is itself a vector space under the same operations of vector addition and scalar multiplication. It must satisfy the conditions that the sum of any two vectors in the subset is also in the subset, and the product of any scalar from the underlying field and a vector in the subset is also in the subset.
What is the dual vector space?
-The dual vector space, denoted as V*, is the set of all linear functionals (co-vectors) on the original vector space V. It is a vector space itself when equipped with the operations of pointwise addition and scalar multiplication.
What is a tensor product and how is it defined?
-A tensor product, denoted by T ⊗ S, is a way to construct a new tensor from given tensors T and S. The tensor product is defined as a tensor of valence p + r and q + s, where T has valence pq and S has valence rs. It is constructed by taking T and 'eating' as many vectors and co-vectors as it can, followed by S eating the remaining vectors and co-vectors.
What is the significance of the tensor space in linear algebra?
-The tensor space is significant in linear algebra as it provides a framework for extending the concepts of vectors and linear maps to higher dimensions. Tensors can capture more complex relationships between geometric and algebraic structures, which is crucial in various applications, including physics and engineering.
What is the role of a basis in a vector space?
-A basis in a vector space serves as a fundamental set of vectors that can be used to express any vector within the space as a unique linear combination. It is essential for constructing coordinates, defining dimensions, and performing calculations within the vector space.
How does the concept of dimension relate to the basis of a vector space?
-The dimension of a vector space is defined as the cardinality (size) of a basis for that space. It provides a measure of the 'size' or the number of independent directions in the space. If the basis is finite, the vector space is said to be finite-dimensional, and the dimension is the number of vectors in the basis.
What is the Einstein summation convention, and how is it used?
-The Einstein summation convention is a notational convention used primarily in field theory and linear algebra. It states that when an index variable appears twice in a single term and is not otherwise defined, it implies that we are summing over all of its possible values. This convention allows for more compact expressions of equations involving tensors and matrices.
Outlines
📚 Introduction to Vector Spaces and Fields
The video begins with a review of vector spaces, emphasizing the foundational role of fields in their construction. It explains that a vector space is an algebraic structure with a field, denoted as K, which is equipped with two operations, addition and multiplication, satisfying specific properties. The distinction between a physicist's and mathematician's definition of a field is highlighted. The video also introduces the concept of a ring, which is similar to a field but with different properties, and notes the importance of these structures in later discussions on modules.
🔢 Understanding Algebraic Structures: Fields and Rings
The script delves into the properties of fields and rings, using examples from high school mathematics to illustrate these concepts. It explains that while every field is a ring, not every ring is a field. The video uses the example of negative integers to show a commutative ring without multiplicative inverses. It also touches upon matrix operations over real numbers to demonstrate a non-commutative ring. The importance of these structures in creating vector spaces is reiterated.
📐 Defining Vector Subspaces and Linear Maps
The video introduces the concept of a vector subspace, explaining that it is a subset of a vector space that is closed under the operations of addition and scalar multiplication. The properties that define a subspace are discussed. Linear maps, or homomorphisms, are then defined as structure-preserving maps between vector spaces. The script outlines the properties of linear maps, including additivity and scalar multiplication, and introduces the concept of a vector space isomorphism.
🔄 Operations on Vector Spaces and the Dual Space
The video explores operations that can be performed on vector spaces, such as defining the set of all linear maps between two vector spaces, which can itself be made into a vector space. The script discusses the addition and scalar multiplication operations on this new space, called the dual space, and how it can be constructed. The importance of understanding the dual space in the context of linear algebra is highlighted.
🧲 Tensor Product and Multilinear Maps
The concept of tensor products is introduced, explaining how they can be used to construct new tensors from existing ones. The script defines a tensor product as a multilinear map that takes multiple copies of a vector space and its dual, and maps them to a scalar. The properties of tensor products and their role in creating higher-rank tensors are discussed.
🔗 Isomorphisms and the Importance of Dimension
The video discusses isomorphisms in the context of vector spaces, highlighting that the dual of the dual of a vector space is isomorphic to the original space, but only if the space is finite-dimensional. The script also touches upon the concept of tensor spaces and their isomorphism to endomorphisms on the dual space. The importance of considering the dimension of a vector space when working with isomorphisms and dual spaces is emphasized.
📏 Defining Dimension and Basis in Vector Spaces
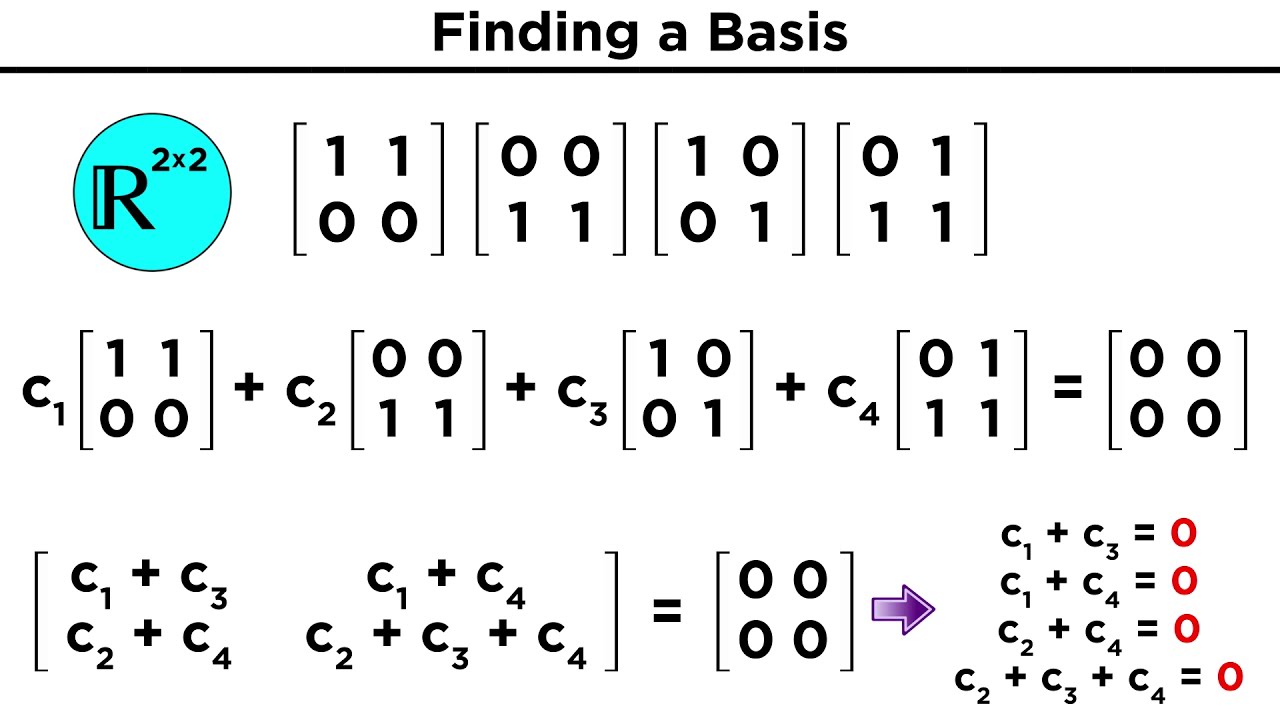
The script explains the concept of dimension in vector spaces, defining it as the cardinality of a basis set. It distinguishes between finite and infinite-dimensional spaces and discusses the role of a basis in generating a vector space. The properties of a basis, including linear independence and the ability to express any vector in the space as a linear combination of basis vectors, are covered in detail.
🧬 Change of Basis and Components of a Tensor
The video addresses the process of changing bases in a vector space and the impact it has on the components of vectors and tensors. It explains how the components of a tensor transform under a change of basis and introduces the concept of tensor density. The script also discusses the use of matrices to represent the change of basis and the resulting transformation of tensor components.
🔍 Induced Basis and Dual Vector Spaces
The script delves into the concept of an induced basis, particularly in the context of dual vector spaces. It explains how choosing a basis for a vector space leads to an induced basis for its dual space, satisfying certain conditions. The importance of this induced basis in simplifying calculations and the role of the dual basis in defining tensor components are highlighted.
📈 Tensor Components and Matrix Representation
The video discusses how to represent tensors using matrices once a basis has been chosen. It explains the relationship between the components of a tensor, the chosen basis, and how these components can be used to reconstruct the tensor. The script also touches upon the representation of endomorphisms as matrices and the implications of matrix multiplication in terms of endomorphism composition.
🔗 Transformation Rules and Abstract Tensors
The script provides transformation rules for tensors under a change of basis, emphasizing the need to understand where indices are placed and how they transform. It discusses the abstract nature of tensors and the importance of reconstructing tensors from their components. The video also cautions against the temptation to rely on component-based notation, advocating for a basis-free understanding of tensors.
📊 Determinants, Volume Forms, and Tensor Densities
The video concludes with a discussion on determinants, volume forms, and tensor densities. It defines the determinant of an endomorphism and explains its relationship with top forms and volume in a vector space. The script also addresses the concept of tensor densities and how they relate to determinants, providing insight into their role in physics and mathematics.
Mindmap
Keywords
💡Vector Space
💡Field
💡Algebraic Structure
💡Linear Map
💡Tensor
💡Dual Vector Space
💡Basis
💡Dimension
💡Endomorphism
💡Change of Basis
💡Determinant
Highlights
A vector space is built on a structure called a field, which is an algebraic concept in mathematics.
An algebraic field is a set K with two operations, plus and times, satisfying certain properties like commutativity and associativity.
Every field is a ring, but not every ring is a field, highlighting the distinction between these algebraic structures.
The concept of a module over a ring is introduced as a generalization of a vector space, with the underlying field replaced by a ring.
Vector spaces and their duals are discussed, emphasizing the isomorphism between V and V** for finite-dimensional vector spaces.
The tensor product of vector spaces is defined, allowing the construction of new tensors from existing ones.
The importance of multilinearity in tensor products is explained, noting that tensors are linear in each entry independent of the others.
The construction of tensor spaces as a set is validated using the principle of restricted comprehension.
The Einstein summation convention is introduced for simplifying the notation of tensor components and their manipulations.
The transformation rules for tensor components under a change of basis are derived, emphasizing the role of the basis in determining tensor representations.
The determinant is defined for endomorphisms on a finite-dimensional vector space, providing a scalar value that is invariant under changes of basis.
The concept of a top form and its role in defining volume in a vector space is discussed, highlighting its importance in the context of determinants.
The difference between determinants of endomorphisms and bilinear forms is clarified, noting that the latter is not well-defined without additional structure.
The use of bundles in mathematics is alluded to as a way to formalize concepts that are not well-defined under change of basis, such as tensor densities.
The importance of constructing mathematical objects without an initial choice of basis is emphasized for the sake of generality and validity across different bases.
The dual basis is introduced as a convenient tool for simplifying calculations involving tensor components in the context of finite-dimensional vector spaces.
The distinction between the abstract concept of a vector space and the concrete representation of vectors through their components with respect to a basis is highlighted.
The role of linear maps, or homomorphisms, in preserving the structure of vector spaces is discussed, particularly in relation to isomorphisms and the classification of vector spaces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: