Lecture 13: More on Scattering
TLDRIn this educational video, the professor delves into the concept of coherence states, particularly in the context of a quantum harmonic oscillator. He explains the ground state's evolution and how displacement affects its temporal behavior. The lecture then transitions to scattering theory, illustrating how particles with energy below or above a potential barrier behave, challenging classical predictions. The discussion includes transmission and reflection probabilities, emphasizing quantum mechanics' departures from classical physics, and concludes with the implications of these phenomena for understanding potentials in physical systems.
Takeaways
- 📚 The lecture discusses the concept of coherence states, particularly in relation to the harmonic oscillator, and how they are treated in quantum mechanics.
- 🌟 Coherence states are introduced as a special type of quantum state that retains a Gaussian shape as it evolves, resembling classical particle behavior.
- 🔍 The professor delves into the mathematical representation of these states, explaining how they are eigenstates of the annihilation operator and their connection to Fourier modes.
- 📈 The script touches on the topic of scattering, explaining the quantum mechanical prediction of particle transmission and reflection probabilities when interacting with a potential barrier.
- 🚀 The classical prediction for particle transmission is contrasted with the quantum mechanical result, highlighting the differences, especially at energies close to the barrier height.
- 🔧 The lecture uses algebraic manipulation and problem-solving techniques to derive the transmission and reflection coefficients for a particle encountering a potential step.
- 📉 The importance of normalization and the conservation of probability in quantum mechanics are emphasized, with the sum of transmission and reflection probabilities equaling one.
- 🤔 The script raises questions about the physical interpretation of the mathematical results, inviting students to ponder the deeper meanings behind the formulas.
- 📊 The professor suggests using computational tools like Mathematica to simplify the algebra involved in quantum mechanics problems, advocating for a balance between analytical skills and technology use.
- 🔬 The lecture concludes with a discussion on tunneling, a quantum phenomenon where particles can transmit through classically forbidden barriers, and its exponential dependence on barrier width.
- 😄 A humorous anecdote about a misplaced car is shared to illustrate the concept of quantum tunneling, albeit in a non-scientific context, highlighting the playful side of scientific discussion.
Q & A
What is the main topic discussed in the lecture?
-The main topic discussed in the lecture is coherence states, particularly in the context of the harmonic oscillator, and how they relate to classical particle behavior in quantum mechanics.
What is a coherent state in the context of quantum mechanics?
-A coherent state is a quantum state of a harmonic oscillator that behaves classically, maintaining a Gaussian wave function shape as it evolves over time, primarily through translations.
What is the ground state of a harmonic oscillator and how does its wave function evolve over time?
-The ground state of a harmonic oscillator is its lowest energy state, characterized by a Gaussian wave function, which is a minimum uncertainty wave packet. Over time, it evolves by changing its phase while maintaining its Gaussian shape.
What happens to a Gaussian wave function when it is displaced in a harmonic oscillator potential?
-When a Gaussian wave function is displaced in a harmonic oscillator potential, it evolves over time by translating its position while maintaining its Gaussian shape, similar to the behavior of a classical particle.
What is the significance of the annihilation operator in the context of coherent states?
-The annihilation operator is significant because coherent states are eigenstates of this operator. Acting on a coherent state with the annihilation operator yields a constant times the same wave function, which is a defining property of coherent states.
How does the professor explain the evolution of a displaced Gaussian wave function in a harmonic oscillator?
-The professor explains that a displaced Gaussian wave function evolves by expanding it in the basis of energy eigenstates, each of which evolves with a phase. The overall state evolves by summing these phases, resulting in a superposition that changes over time due to interference effects.
What is a squeeze state and how is it related to a coherent state?
-A squeeze state is a quantum state of a harmonic oscillator where the uncertainties in position and momentum are modified compared to the ground state. It is related to a coherent state in that it also exhibits classical-like behavior, but with different uncertainty properties.
What is the role of the potential in determining the behavior of a quantum particle in a scattering experiment?
-The potential determines the scattering behavior of a quantum particle by influencing the transmission and reflection probabilities. The shape and height of the potential barrier affect whether the particle is transmitted, reflected, or exhibits tunneling effects.
How does the transmission probability of a quantum particle change as it interacts with a potential barrier?
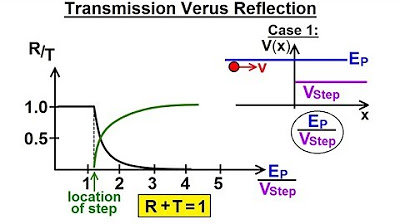
-The transmission probability of a quantum particle depends on the energy of the particle relative to the height of the potential barrier. For energies below the barrier, the probability is exponentially small, indicating tunneling effects. For energies above the barrier, the probability can approach 1, indicating almost certain transmission.
What is the difference between the classical and quantum predictions for the transmission of a particle with energy slightly above a potential barrier?
-Classically, it is predicted that a particle with energy slightly above a potential barrier will always transmit across the barrier. Quantum mechanically, however, the transmission probability is not 1 but rather a value less than 1, indicating that there is a significant chance the particle will not transmit, even if its energy is slightly above the barrier.
What is the significance of the reflection and transmission coefficients in scattering experiments?
-The reflection and transmission coefficients are significant because they describe the likelihood of a particle being reflected back or transmitted through a potential barrier, respectively. These coefficients contain information about the potential's shape and can be used to deduce properties of the potential.
How can one deduce the shape of an unknown potential by studying the transmission probabilities?
-By studying the transmission probabilities as a function of energy, one can infer the shape of an unknown potential. Features such as resonances or specific transmission peaks can indicate the presence of certain potential structures, such as barriers or wells.
What is the mathematical expression for the transmission probability of a particle with energy greater than the potential barrier height?
-The transmission probability for a particle with energy greater than the potential barrier height is given by a complex expression involving trigonometric functions and the ratio of the particle's wave numbers inside and outside the barrier.
What is the physical interpretation of the transmission probability being less than 1 even when the particle's energy is greater than the potential barrier?
-The transmission probability being less than 1 even when the particle's energy is greater than the potential barrier indicates that there is a chance for the particle to be reflected back rather than completely transmitted. This is a quantum effect that does not have a classical analogue.
What is the relationship between the transmission probability and the phase shift in scattering experiments?
-The transmission probability and the phase shift are related in that they both contain information about the scattering process. The phase shift, in particular, provides additional information beyond the transmission probability, which is necessary to uniquely determine the potential.
What is the significance of the dimensionless parameters g0 and epsilon in the context of the transmission probability?
-The dimensionless parameters g0 and epsilon are significant as they simplify the expression for the transmission probability and make it easier to analyze and interpret. g0 is a measure of the barrier's strength relative to the particle's energy, and epsilon is the ratio of the particle's energy to the barrier height.
How does the transmission probability behave at very low and very high energies relative to the potential barrier?
-At very low energies (when epsilon is much less than 1), the transmission probability is exponentially small due to tunneling effects. At very high energies (when epsilon is much greater than 1), the transmission probability approaches 1, indicating that the barrier has negligible effect on the particle's transmission.
What is the physical explanation for the phenomenon of tunneling?
-Tunneling is a quantum mechanical phenomenon where a particle can transmit through a potential barrier even if its energy is less than the barrier height. This occurs due to the wave-like nature of particles, allowing them to exist in classically forbidden regions with a non-zero probability.
What is the effect of the barrier's width on the tunneling amplitude?
-The tunneling amplitude decreases exponentially with increasing barrier width. This means that wider barriers are less likely to be penetrated by particles through tunneling.
What are the implications of the story about the misplaced car in the context of quantum mechanics?
-The story serves as a humorous anecdote illustrating the misunderstanding of quantum mechanics principles by non-physicists. It highlights the fact that quantum effects like tunneling do not apply to macroscopic objects like cars in the same way they do for microscopic particles.
Outlines
📚 Introduction to Coherence States and MIT OpenCourseWare
The script begins with an introduction to the MIT OpenCourseWare initiative, which offers free educational resources under a Creative Commons license. The professor encourages donations to support this cause and directs interested parties to the website. The lecture then transitions into a discussion about coherence states, a topic previously introduced in optional problems related to the harmonic oscillator. The professor explains the basic concept of coherence states, which are Gaussian wave functions that remain coherent over time, and their significance in quantum mechanics.
🌀 Coherence States and the Time Evolution of the Harmonic Oscillator
This paragraph delves deeper into the properties of coherence states, particularly their behavior under time evolution. The professor discusses how a displaced Gaussian wave function, representing the ground state of a harmonic oscillator, evolves over time. Despite the complexity of its phase, the probability distribution of this state remains a translating Gaussian, a property that distinguishes it from generic wave functions. The paragraph also explores the concept of eigenstates of the annihilation operator and how they relate to coherent states.
🔬 Quantum Mechanics and the Behavior of Coherent States
The script continues to explore the behavior of coherent states in quantum mechanics, emphasizing their classical-like behavior despite being quantum in nature. The professor discusses how the momentum of a coherent state changes over time and how its phase is related to its spatial rate of change. The paragraph also touches on the concept of squeeze states, which are variations of coherent states with altered uncertainty relations, and their periodic nature.
🚀 Quantum Scattering and the Transmission Through Potential Barriers
The focus shifts to quantum scattering, where a particle with mass m is considered against a potential barrier. The classical prediction for particle transmission is contrasted with the quantum mechanical approach, which involves solving the Schrödinger equation for wave functions in the presence of a potential. The professor outlines the process of matching wave function solutions to describe scattering and the significance of transmission and reflection probabilities.
📉 Analyzing Quantum Transmission and Reflection Probabilities
This paragraph discusses the detailed analysis of transmission and reflection probabilities in quantum scattering. The professor derives expressions for these probabilities when the energy of the particle is above the potential barrier. The transmission probability is shown to approach 1 as the energy becomes much larger than the potential, aligning with classical predictions. The relationship between the reflection and transmission coefficients is also explored.
🤔 Reflections on Quantum vs. Classical Scattering
The script presents a thought experiment comparing quantum mechanical scattering with classical physics. The professor uses the analogy of a car rolling up a hill to illustrate the difference between classical and quantum predictions. In classical physics, the car would either make it over the hill or not, with no possibility of reflection back down the hill. In contrast, quantum mechanics allows for the particle to be reflected even when it has enough energy to overcome the barrier, highlighting the probabilistic nature of quantum phenomena.
🔍 Deep Dive into Quantum Transmission Probability
The professor scrutinizes the quantum transmission probability, addressing the question of why it is squared when calculating probabilities. The explanation involves the quadratic nature of probability density in relation to the wave function and the current. The paragraph also corrects a typo from previous notes and emphasizes the importance of checking calculations against physical reasonableness.
🧲 Exploring the Quantum Mechanical Barrier
This paragraph examines the implications of quantum scattering for understanding the potential barriers that particles encounter. The professor suggests that by measuring transmission probabilities as a function of energy, one can deduce the shape of the potential barrier. The concept of phase shift is introduced as an essential aspect of this analysis, and the idea that scattering experiments can reveal the internal structure of a system is discussed.
🔬 Investigating the Effects of Potential Barriers on Scattering
The script concludes with a detailed investigation of how potential barriers affect scattering. The professor discusses the conditions for different types of scattering experiments and how they relate to the coefficients of the wave function. The importance of understanding the transmission and reflection coefficients is highlighted, as they contain all the information needed to characterize the scattering process.
📚 Summary of Quantum Scattering Analysis
The final paragraph provides a summary of the quantum scattering analysis, emphasizing the ability to deduce the form of a potential barrier based on transmission probabilities. The professor outlines the steps involved in the analysis and encourages the use of computer algebra systems to simplify the algebraic calculations. The potential of quantum mechanics to reveal the properties of systems through scattering experiments is highlighted.
😅 A Quantum Tunneling Joke
The script ends with a humorous anecdote about a friend who misplaced her car and jokingly attributed its disappearance to quantum tunneling. The story serves as a light-hearted conclusion to the lecture, illustrating the tendency to attribute everyday occurrences to quantum phenomena, despite the macroscopic scale at which such effects are negligible.
Mindmap
Keywords
💡Coherence States
💡Harmonic Oscillator
💡Minimum Uncertainty Wave Packet
💡Annihilation Operator
💡Quantum Superposition
💡Classical Particle Behavior
💡Transmission Probability
💡Potential Barrier
💡Quantum Tunneling
💡Squeeze States
💡Reflection Probability
Highlights
Introduction to coherence states and their significance in quantum mechanics.
Coherence states as eigenstates of the annihilation operator and their connection to the harmonic oscillator.
The Gaussian wave function of the ground state of a harmonic oscillator and its time evolution.
Displacement of the ground state and its effect on the time evolution of the system.
Coherent states maintaining a Gaussian shape while oscillating, resembling classical particle behavior.
The concept of minimum uncertainty wave packets and their relevance to coherent states.
Optional problems for deeper exploration of the harmonic oscillator's structure and coherence states.
Discussion on the evolution of displaced Gaussian states and their coherence over time.
The role of Fourier transforms in understanding the time-independent nature of momentum distribution.
Explanation of how coherent states are superpositions of energy eigenstates.
Properties of squeeze states and their distinction from coherent states in terms of uncertainty.
The impact of potential changes on the harmonic oscillator's ground state and its subsequent evolution.
Transmission and reflection probabilities in quantum scattering and their classical predictions.
Quantum mechanical calculation of transmission and reflection for a particle incident on a potential barrier.
The surprising result that transmission probability is not a step function and its implications.
The relationship between the quantum mechanical transmission probability and classical predictions at high energies.
The condition that reflection and transmission probabilities must sum up to one for probability conservation.
The difference between quantum and classical predictions for scattering off a potential barrier.
Transcripts
Browse More Related Video

Advanced Quantum Mechanics Lecture 3
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (62 of 92) Transmission vs Reflection

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

Statistical Mechanics Lecture 7

23. Quantum Mechanics V: Particle in a Box

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (61 of 92) Reflection & Transmission
5.0 / 5 (0 votes)
Thanks for rating: