Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (62 of 92) Transmission vs Reflection

Michel van Biezen
20 Apr 201804:35
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the intriguing world of quantum mechanics, contrasting the behavior of particles at a potential barrier with classical expectations. It explains that contrary to macroscopic predictions, not all particles are reflected or transmitted at once; instead, there's a gradual transition. The graph illustrates that even when a particle's energy is less than the barrier's potential, some can tunnel through, and as the energy exceeds the barrier, transmission increases while reflection decreases, not instantaneously but progressively. The total probability of reflection and transmission remains 100%, reflecting the probabilistic nature of quantum events.

Takeaways
  • 🌟 Quantum mechanics differs from classical physics in how particles interact with barriers or potential steps.
  • 🔍 In the macro world, particles with energy greater than a barrier will pass through, while those with less energy will be reflected.
  • 📈 The graph illustrates the percentage of particles transmitted or reflected based on the energy-to-barrier potential ratio.
  • 🚧 When a particle's energy is less than the barrier, there is still a possibility for penetration, potentially leading to quantum tunneling.
  • 🌈 The green line on the graph shows that transmission and reflection of particles are not immediate or step functions in the quantum world.
  • 🔽 As the energy-to-barrier ratio increases, more particles are transmitted and fewer are reflected.
  • 📉 The reflection of particles decreases rapidly as the energy exceeds the barrier potential.
  • 💯 By the time the energy-to-barrier ratio reaches 2:1, almost all particles are transmitted and almost none are reflected.
  • 🔄 The total probability of particles reflected and transmitted must equal 1, maintaining the conservation of probability.
  • 📚 The study of boundary regions and the behavior of transmission and reflection in quantum mechanics is complex and will be further explored.
Q & A

  • What is the main topic of the transcript?

    -The main topic of the transcript is the behavior of quantum mechanical events involving small particles encountering barriers or potential steps.

  • How does the classical world view differ from the quantum world in terms of particles encountering barriers?

    -In the classical world, if a particle's energy is greater than the barrier's potential, it is expected to continue past the barrier, whereas in the quantum world, there is not a 100% transmission rate due to the possibility of reflection and tunneling.

  • What happens when a particle's energy is less than the potential of the barrier in the quantum world?

    -In the quantum world, even if a particle's energy is less than the potential of the barrier, there is still a possibility for the particle to penetrate through the barrier, known as quantum tunneling.

  • How is the graph in the transcript structured?

    -The graph has the ratio of the particle's energy to the potential of the step or barrier on the horizontal axis and the percentage or fraction of particles reflected or transmitted on the vertical axis.

  • What does the green line on the graph represent?

    -The green line represents the percentage of particles that are transmitted past the barrier or step as the ratio of the particle's energy to the potential increases.

  • What is the significance of the total reflected waves plus the total transmitted waves equaling 1?

    -It signifies that the total probability of all particles incident on the barrier or step, either reflected or transmitted, adds up to 100%, which is a fundamental principle in quantum mechanics.

  • Why is the transmission of particles not an immediate jump when the particle's energy exceeds the barrier's potential?

    -The transmission is not an immediate jump because there is still a certain percentage of particles that will be reflected, and the percentage of transmitted particles increases gradually as the energy ratio increases.

  • What happens to the reflection of particles when the energy of the particle is much greater than the potential of the barrier?

    -When the particle's energy is significantly greater than the potential of the barrier, the reflection of particles drops off rapidly, and almost none of the particles are reflected, with virtually all being transmitted.

  • How does the graph illustrate the concept of quantum tunneling?

    -The graph illustrates quantum tunneling by showing that even when the particle's energy is less than the potential of the barrier, there is still a non-zero percentage of particles being transmitted, indicating that some particles can tunnel through the barrier.

  • What will be studied further in relation to the boundary regions?

    -Further studies will focus on understanding the boundary regions' appearance and how transmission and reflection take place, including the extent, depth, and rate at which the probabilities drop off as particles interact with the barrier.

Outlines
00:00
🌟 Quantum Mechanics and Particle Behavior

This paragraph introduces the fascinating world of quantum mechanics, focusing on the behavior of small particles when encountering barriers or potential steps. It explains the contrast between macroscopic expectations and quantum outcomes, where particles with energy less than the barrier can still penetrate and tunnel through, a phenomenon not observed in the macro world. The discussion revolves around a graph that illustrates the percentage of particles reflected and transmitted based on the energy-to-barrier potential ratio. The graph shows that as this ratio increases, more particles are transmitted, and fewer are reflected, deviating from a step function as might be expected classically. The total probability of reflection and transmission equals 1, adhering to the quantum mechanics principle that the sum of reflected and transmitted particles equals 100% of those incident on the barrier or step.

Mindmap
Keywords
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. In the video, it is the basis for understanding the unusual behavior of particles when they interact with barriers or potential steps, highlighting the difference between classical physics and quantum physics.
💡Energy
In the context of the video, energy refers to the amount of force or work a particle possesses. It is a crucial factor in determining whether a particle will be transmitted or reflected when encountering a barrier. The energy of a particle is compared to the potential of the barrier to predict its behavior.
💡Barrier
A barrier in this context is an obstacle or a potential step that a particle may encounter. It represents a change in the potential energy landscape that can affect the particle's trajectory. The interaction between particles and barriers is a key focus of the video, illustrating the principles of quantum mechanics.
💡Potential Step
A potential step is a sudden change in the potential energy landscape that a particle may encounter. It is similar to a barrier but often implies a change in the potential energy rather than a complete obstruction. The behavior of particles at a potential step is used in the video to demonstrate the principles of quantum mechanics.
💡Transmission
Transmission in the video refers to the process by which particles get past a barrier or potential step. It is a key phenomenon in quantum mechanics where particles can pass through barriers that they classically shouldn't be able to overcome, given their energy.
💡Reflection
Reflection, as used in the video, describes the phenomenon where particles bounce back after encountering a barrier or potential step. In quantum mechanics, even particles with less energy than the barrier's potential can reflect, though the percentage of reflected particles changes with the energy-barrier ratio.
💡Graph
The graph mentioned in the script is a visual representation of the relationship between the energy of particles and the potential of a barrier or step. It shows the percentage of particles that are transmitted or reflected at different energy-to-barrier potential ratios, providing insights into quantum mechanical events.
💡Tunneling
Tunneling is a quantum mechanical effect where particles can pass through a barrier that they classically shouldn't be able to overcome. It is a phenomenon that occurs when the barrier is thin enough and the particle's energy is close to the potential of the barrier, allowing for a small probability of penetration.
💡Probability
In the context of the video, probability refers to the likelihood of a particle being transmitted or reflected when interacting with a barrier. The total probability of all possible outcomes (transmission and reflection) must equal 1, reflecting the certainty of the event occurring in one of these two ways.
💡Macro World
The macro world refers to the everyday, human-scale world of objects and events that are observable without the need for specialized equipment. In the video, it contrasts with the quantum world by highlighting the differences in how particles behave at larger scales compared to the microscopic scale.
💡Micro World
The micro world, or quantum world, refers to the realm of particles and forces at extremely small scales, such as atoms and subatomic particles. This world operates under the principles of quantum mechanics, which often result in counterintuitive phenomena not observed in the macro world.
Highlights

Quantum mechanical events with very small particles are discussed.

A graph provides insight into particle behavior when encountering barriers or potential steps.

In the macro world, particles with energy greater than the barrier continue, albeit with less energy.

In the quantum world, particles with less energy than the barrier do not all stop and get reflected back.

The vertical axis represents the percentage of particles reflected or transmitted past a boundary.

The horizontal axis shows the ratio of particle energy to the potential of the step or barrier.

If the energy ratio is greater than one, particles are expected to be transmitted.

When the energy ratio is less than one, particles are expected to be reflected.

Quantum mechanics reveals that even with less energy, some particles can penetrate barriers (tunneling).

The green line on the graph shows that particle transmission does not jump immediately with increased energy.

As the energy ratio increases, more particles are transmitted and fewer are reflected.

The transition is not a step function as expected in the macro world.

Even when a particle's energy is greater than the barrier, not all particles get past it; some are reflected.

By the time the energy ratio is 2 to 1, almost no particles are reflected, and almost all are transmitted.

The total reflected waves plus the total transmitted waves must equal 1, maintaining the total probability.

The study will further explore the boundary regions and how transmission and reflection occur.

The visualization helps understand the complex behavior of particles at the boundary.

Transcripts

Browse More Related Video

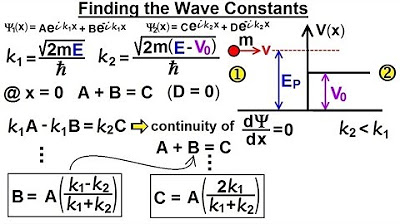
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (65 of 92) Wave Constants B=? C=?

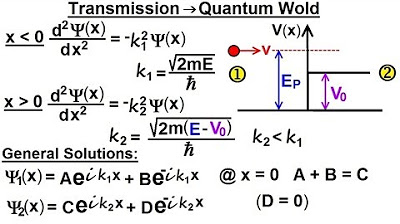
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

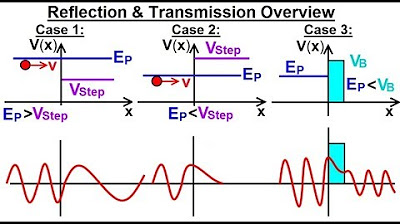
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (61 of 92) Reflection & Transmission

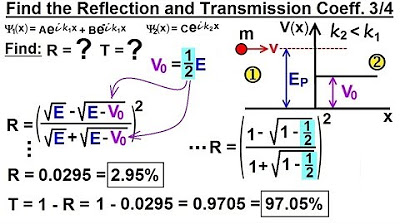
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (73 of 92) R=? T=? V0=(1/2)E (Ex. 3 of 4)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (74 of 92) R=? T=? V0=(3/4)E,.(Ex. 4 of 4)

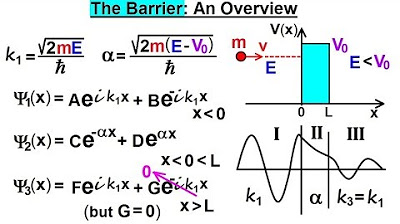
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsParticle BehaviorBarrier InteractionEnergy RatiosQuantum TunnelingPhysics EducationMicroscopic EventsWave TransmissionProbability TheoryScientific Visualization