Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (61 of 92) Reflection & Transmission

Michel van Biezen
19 Apr 201803:21
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explores the behavior of particles encountering barriers in quantum mechanics. It discusses three scenarios: when a particle's energy exceeds a potential step and experiences reflection and transmission with a longer wavelength; when its energy is insufficient to overcome the step, leading to full reflection; and the possibility of particles tunneling through finite-width barriers. The video promises to delve into calculating the probabilities of reflection and transmission in these cases, offering insights into the quantum world's deviations from classical physics.

Takeaways
  • 🌟 Particles encountering barriers can be reflected or transmitted depending on their energy relative to the barrier's potential.
  • 🚀 If a particle's energy exceeds the step potential, it may continue but with a longer wavelength and reduced velocity.
  • 📉 When a particle's energy is less than the step potential, it is classically reflected, but quantum mechanics allows for a small probability of transmission.
  • 🛡️ Quantum mechanics predicts that particles with energy less than a barrier's potential can tunnel through finite-width barriers, with an exponentially decreasing probability.
  • 📊 The probability of a particle tunneling through a barrier decreases exponentially with the barrier's width and the energy of the particle.
  • 🌈 Wavelength changes are associated with energy loss, which is seen when particles are transmitted over potential steps or through barriers.
  • 🔄 Reflection and transmission are possible in all three scenarios: when energy is greater than the step, less than the step, and when tunneling through a finite barrier.
  • 🧠 Understanding the quantum behavior of particles at potential barriers requires calculating penetration distances and probabilities at various points.
  • 🎯 The script outlines a series of explorations into how energy and potential barriers interact and influence particle behavior.
  • 🔍 The upcoming videos will delve into the calculations behind reflection and transmission probabilities in different energy-potential scenarios.
Q & A

  • What happens when a particle encounters a temporary barrier like an engaged step?

    -When a particle encounters a temporary barrier, there are two main possibilities. If the particle's energy is greater than the potential of the step, it may continue on or be reflected, and if transmitted, it will have a longer wavelength due to the loss of some energy. If the particle's energy is less than the step's potential, it will be reflected according to classical understanding, but in quantum mechanics, there's a small probability that it can continue into the barrier for a certain distance.

  • What is the effect of a particle losing energy when it encounters a potential step?

    -When a particle loses energy upon encountering a potential step, its wavelength becomes longer. This is because the energy is converted into a longer wavelength, resulting in a slower velocity for the particle.

  • How does the energy of a particle compare to the potential step affect its behavior?

    -If the particle's energy is greater than the potential step, it may continue, be reflected, or transmitted with a longer wavelength. If the energy is less, classically it would be fully reflected, but quantum mechanically, there's a small chance it can tunnel through the barrier.

  • What is the quantum mechanical phenomenon where particles can pass through barriers despite having less energy than the barrier's potential?

    -The quantum mechanical phenomenon where particles can pass through barriers with less energy than the barrier's potential is known as quantum tunneling.

  • What happens when a particle encounters a barrier of finite width?

    -When a particle encounters a barrier of finite width, if its energy is less than the barrier's potential, it would normally be fully reflected. However, if the barrier is thin enough, the particle could potentially make its way through and continue on the other side, exhibiting an exponential decay in probability as it penetrates the barrier.

  • How does the thickness of a barrier affect the particle's ability to tunnel through it?

    -The thinner the barrier, the higher the probability that a particle will be able to tunnel through it, even if its energy is less than the potential of the barrier.

  • What are the two main outcomes when a particle encounters a potential step with greater energy?

    -When a particle encounters a potential step with greater energy, it can either be reflected or transmitted. Transmission results in a longer wavelength due to the loss of energy.

  • What is the probability of a particle tunneling through a barrier in quantum mechanics?

    -The probability of a particle tunneling through a barrier in quantum mechanics is small and decreases exponentially with the distance it penetrates into the barrier, eventually approaching zero.

  • How will the transmission and reflection of particles be calculated in different scenarios presented in the script?

    -The transmission and reflection of particles in different scenarios will be calculated by examining cases where the energy is greater than the potential step, where the energy is less than the potential step, and where the energy is smaller than the potential of a finite-width barrier. Each case will have its specific calculations for determining the extent of reflection and transmission.

  • What is the significance of the exponential decay in the context of a particle penetrating a barrier?

    -The exponential decay signifies the rapidly decreasing probability of a particle penetrating a barrier as it moves further into it. This reflects the increasing improbability of quantum tunneling as the barrier becomes more substantial.

  • What can we expect to learn in the upcoming videos based on the script?

    -In the upcoming videos, we can expect to learn about the specific calculations and behaviors of particles in various scenarios, such as when their energy is greater than the potential step, when it is less, and when they encounter a finite-width barrier that could allow for tunneling.

Outlines
00:00
🌟 Quantum Mechanics: Particle-Barrier Interactions

This paragraph introduces the topic of quantum mechanics, specifically focusing on how a particle reacts when encountering a barrier or an increase in potential. It discusses three scenarios: (1) when a particle's energy is greater than the potential step, leading to possible reflection and transmission with a longer wavelength due to energy loss; (2) when a particle's energy is less than the potential step, resulting in total reflection; and (3) when a finite-width barrier is present, allowing some particles to tunnel through. The paragraph emphasizes the probabilistic nature of quantum mechanics, contrasting it with classical physics, and sets the stage for further exploration of these phenomena in upcoming videos.

Mindmap
Keywords
💡particle
A particle, in the context of the video, refers to a small, distinct mass or object that has a defined energy and interacts with its environment. It is the subject of study as the video explores how it reacts when encountering barriers or changes in potential energy. For example, the script discusses how a particle may be reflected or transmitted when it encounters a step up in potential energy.
💡barrier
A barrier in this context is an obstacle or a physical limitation that a particle may encounter, which can be temporary or of finite width. The video discusses how particles react differently to barriers, such as being reflected, transmitted, or tunneling through, depending on the energy of the particle and the properties of the barrier.
💡potential energy
Potential energy is the stored energy an object has due to its position in a force field, such as a gravitational or electric field. In the video, changes in potential energy are critical in determining a particle's behavior when it encounters barriers, like steps or finite barriers, and how much energy is lost or gained during these interactions.
💡reflection
Reflection, in the context of the video, refers to the phenomenon where a particle bounces back after encountering a barrier or an increase in potential energy. This is a classical behavior expected when the particle's energy is less than the energy of the barrier, but the video also explores the quantum mechanical possibility of reflection even when the particle's energy is greater.
💡transmission
Transmission is the process by which a particle continues to move through or beyond a barrier, despite the presence of an energy potential higher than its own. In quantum mechanics, this is not just limited to particles with sufficient energy but also includes the phenomenon of quantum tunneling, where particles with lower energy can pass through barriers.
💡wavelength
Wavelength is the distance between two consecutive points in a wave, such as the distance between two crests. In the video, it is mentioned that when a particle's energy decreases due to interaction with a barrier, its wavelength increases, indicating a change in its wave-like properties.
💡quantum mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. The video delves into quantum mechanical phenomena, like tunneling and the probabilistic nature of particle behavior, which differ from classical physics predictions.
💡probability
Probability in this context refers to the likelihood of a particular outcome for a particle when it interacts with a barrier, such as the chance of reflection, transmission, or tunneling. The video explores how quantum mechanics introduces probabilistic behaviors that are not predicted by classical physics.
💡tunneling
Tunneling is a quantum mechanical phenomenon where a particle passes through a potential barrier that it classically should not be able to overcome. This is due to the wave-like nature of particles, which allows them to exist on the other side of the barrier, albeit with a decreasing probability.
💡exponential decay
Exponential decay is a mathematical model that describes a quantity approaching zero at a rate that is proportional to its current value. In the video, this concept is used to describe how the probability of a particle tunneling through a barrier decreases rapidly as it penetrates deeper into the barrier.
💡energy conservation
Energy conservation is the principle that the total energy in an isolated system remains constant over time. In the video, this principle is implicitly considered when discussing how particles lose energy as they interact with barriers, converting it into a longer wavelength, and how this affects their transmission and reflection.
Highlights

Discussion of particle behavior when encountering barriers or potential increases.

Two possibilities for particle interaction with a step potential: reflection or transmission with a longer wavelength due to energy loss.

Quantum mechanics allows for the surprising transmission of particles through barriers, even when their energy is less than the step potential.

In the quantum world, particles can penetrate barriers to a certain extent, with the probability exponentially decreasing to zero.

Exploration of three different scenarios: energy greater than potential step, energy less than potential step, and finite width barriers.

Calculation of penetration distance and probability distribution for particles in quantum mechanics.

Transmission and reflection probabilities vary depending on the energy of the particle and the characteristics of the barrier.

Quantum tunneling is possible when a particle encounters a barrier of finite width, despite classical physics predicting no penetration.

The concept of wave-particle duality and its implications on particle behavior in the presence of barriers.

The velocity of particles decreases as they lose energy, resulting in a longer wavelength after passing through a potential step.

Classical physics predicts 100% reflection for particles with energy less than the barrier, but quantum mechanics introduces the possibility of transmission.

The phenomenon of exponential decay in particle probability as they attempt to penetrate a barrier.

The interplay between particle energy, barrier width, and the potential difference in determining particle behavior.

The upcoming series of videos will delve into the calculations and understanding of reflection and transmission probabilities.

Stay tuned for further exploration of quantum mechanics and particle-barrier interactions.

Transcripts

Browse More Related Video

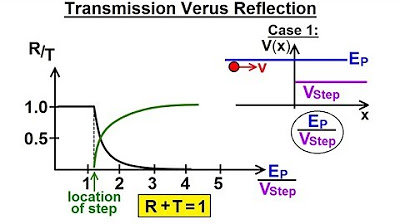
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (62 of 92) Transmission vs Reflection

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (74 of 92) R=? T=? V0=(3/4)E,.(Ex. 4 of 4)

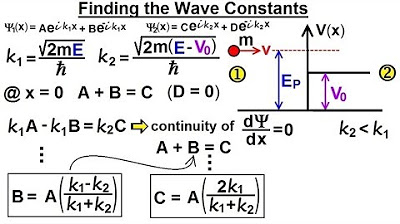
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (65 of 92) Wave Constants B=? C=?

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (71 of 92) R=? T=? V0=(1/4)E (Ex. 1 of 4)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

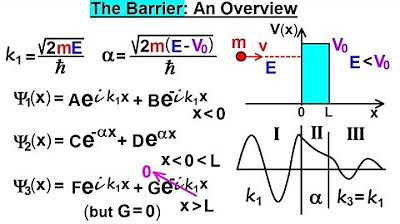
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsParticleBehaviorBarrierPenetrationTunnelingEffectWavelengthChangeEnergyConversionProbabilityCalculationsPhysicsEducationScientificExplorationEducationalContent