2022 Live Review 7 | AP Physics C: Mechanics | Gravitation
TLDRIn this educational video, Angela Jensmold from Diamond Bar High School delves into the concepts of gravitation, focusing on Newton's universal law, gravitational acceleration, potential energy, escape speed, and angular momentum in orbits. She explores Kepler's laws, deriving expressions for satellite orbits and discussing the conservation of angular momentum. The video includes multiple-choice and free-response questions to reinforce understanding, aiming to prepare students for the AP Physics exam.
Takeaways
- 📚 Newton's Universal Law of Gravitation is fundamental to understanding gravitational forces and orbits, stating that every point mass attracts every other point mass with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
- 🌍 Gravitational acceleration can be derived from the law for any planet, showing how gravity changes with distance from the planet's center, not just at the surface.
- 🔋 Gravitational potential energy is expressed as negative GMm/r, where G is the gravitational constant, M and m are the masses of the two objects, and r is the separation between their centers of mass.
- 🚀 Escape speed is the minimum speed needed to break free from a planet's gravitational pull and is independent of the object's mass, depending only on the mass and radius of the planet.
- 🌐 Angular momentum is conserved in orbits where no external torques are acting on the system, such as satellites orbiting above a planet's atmosphere.
- ⏱ Kepler's laws describe the motion of planets around the sun, with the first law stating that orbits are elliptical with the sun at one focus, the second law relating the area swept by the radius vector to time, and the third law connecting the orbital period to the radius of the orbit.
- 🔢 The gravitational constant, G, is a small number (6.67 x 10^-11 N(m/kg)^2), indicating that gravity, though significant in our daily lives, is the weakest of the four fundamental forces in nature.
- 📉 Gravitational force decreases with the square of the distance between two objects, meaning even a slight increase in distance can significantly reduce the force.
- 📈 The escape speed formula shows that it is dependent on the mass of the planet and the radius from the planet's center, but not on the mass of the object being launched.
- 📉 The force of gravity inside a uniformly dense planet on an object moving through a tunnel is proportional to the distance from the center of the planet, with the force being zero at the center.
- ⏳ The time it takes for an object to move from the surface to the center of a planet can be calculated using a differential equation derived from Newton's second law, considering the force of gravity as a function of distance from the center.
Q & A
What is the fundamental principle of Newton's universal law of gravitation?
-Newton's universal law of gravitation states that any two objects with mass attract each other with a force whose magnitude is proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass.
What is the difference between gravitational acceleration (lowercase g) and the universal gravitation constant (capital G)?
-Gravitational acceleration (lowercase g) refers to the acceleration due to gravity experienced by an object, such as on the surface of a planet, while the universal gravitation constant (capital G) is a fundamental constant of nature, approximately equal to 6.67 × 10^-11 N(m/kg)^2, which is used in calculations involving gravitational forces between masses.
Why is the gravitational potential energy between two objects generally negative?
-Gravitational potential energy is generally negative because it is derived from the work done against the attractive gravitational force when objects are moved from an infinite separation (where potential energy is defined as zero) to a finite separation. The negative sign indicates that energy is stored in the system due to the gravitational attraction.
How is the escape speed of a planet derived?
-The escape speed of a planet is derived by considering the energy conservation of a system where an object is launched from the planet's surface to an infinite distance, assuming no external forces act on the system. The escape speed is the speed needed for the object to have zero kinetic energy when it is infinitely far away from the planet.
What is the significance of angular momentum conservation in orbits?
-Conservation of angular momentum in orbits implies that the product of an object's mass, velocity, and radius (mvr) remains constant when no external torques are acting on the system. This principle is crucial for understanding how satellites and other celestial bodies maintain their orbital paths.
What are Kepler's three laws of planetary motion?
-Kepler's first law states that planets move in elliptical orbits with the sun at one focus. The second law, also known as the law of equal areas, states that a line segment joining a planet and the sun sweeps out equal areas during equal intervals of time. Kepler's third law, the law of harmonies, states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.
How does the gravitational acceleration on a planet's surface compare to its value at a height equal to twice the planet's radius?
-The gravitational acceleration at a height equal to twice the radius of a planet is one-ninth of the gravitational acceleration at the planet's surface, assuming the object is outside the planet's atmosphere and the planet's density is uniform.
What determines the escape speed of an object launched from a planet?
-The escape speed of an object launched from a planet is determined solely by the mass of the planet and the radius of the planet from the object, and it is independent of the object's mass.
What happens to the angular momentum of an object moving in an elliptical orbit around the Earth?
-For an object moving in an elliptical orbit around the Earth, assuming no external torques, the angular momentum remains constant because the product of the object's mass, velocity, and radius (mvr) does not change as it orbits.
How can one calculate the orbital speed and period of a satellite in a circular orbit around Jupiter?
-The orbital speed of a satellite in a circular orbit around Jupiter can be calculated using Newton's second law in the radial direction, equating the gravitational force to the centripetal force required for circular motion. The orbital period can then be found by rearranging the formula for speed to solve for the time it takes to complete one orbit.
What would be the effect on the orbit of a satellite if it is launched with a speed slightly faster than required for a circular orbit at the desired altitude?
-If a satellite is launched with a speed slightly faster than required for a circular orbit at the desired altitude, it will end up in an elliptical orbit with Jupiter at one focus, and the semi-major axis of the ellipse will be greater than the radius of the intended circular orbit.
What is the work done by gravity on a sphere dropped from rest at the surface to the center of a non-rotating planet with uniform density?
-The work done by gravity on a sphere dropped from rest at the surface to the center of a non-rotating planet with uniform density is positive and can be calculated by integrating the force of gravity over the distance from the surface to the center, which results in a value proportional to the square of the distance from the center, divided by two.
How can you describe the motion of a sphere that passes through the center of a planet and continues to the opposite surface in a frictionless tunnel?
-The sphere will oscillate back and forth between the two surfaces of the planet without damping, due to the absence of friction and external forces in the tunnel. It will reach maximum speed at the center, where the gravitational force is momentarily zero, and then decelerate as it moves away from the center, only to change direction and repeat the motion.
Outlines
📚 Introduction to Gravitation and Newton's Law
The script begins with an introduction to the topic of gravitation, focusing on Newton's Universal Law of Gravitation, which is foundational to the study of celestial mechanics. Angela Jensmold, a teacher from Diamond Bar High School, California, explains that the law states any two objects with mass attract each other with a force proportional to the product of their masses and inversely proportional to the square of the distance between their centers of mass. The script covers deriving expressions for gravitational acceleration on any planet, gravitational potential energy between any two objects, escape speed, angular momentum conservation in orbits, and Kepler's laws. Special attention is given to distinguishing between the gravitational acceleration (lowercase 'g') and the universal gravitational constant (capital 'G').
🚀 Derivation of Gravitational Potential Energy and Escape Speed
This paragraph delves into the derivation of gravitational potential energy, explaining its negative value in relation to the work done by the gravitational force. The script discusses how the potential energy is calculated as the negative of the work done to move an object from one position to another, given by the formula negative G * m1 * m2 / r, where r is the separation between the centers of mass. The concept of escape speed is introduced, explaining the speed required to move an object to an infinite distance from a planet, derived from the conservation of energy principle. The escape speed is shown to depend solely on the mass of the planet and not the object being launched.
🌌 Angular Momentum Conservation and Kepler's Laws
The script moves on to discuss angular momentum conservation in orbits, stating that in the absence of external torques, the angular momentum of an orbiting object remains constant. This is followed by an explanation of Kepler's laws, starting with the first law that planets move in elliptical orbits with the sun at one focus. The second law, which states equal areas are swept out in equal times, is illustrated with an example. The third law, derived from a force diagram and Newton's second law, quantifies the relationship between the orbital period and the radius of the orbit, showing that the square of the orbital period is proportional to the cube of the semi-major axis of the orbit.
🌍 Application of Gravitational Concepts to Planetary Bodies
The script applies the concepts of gravitational acceleration, escape speed, and Kepler's laws to hypothetical scenarios involving planets with different masses and radii compared to Earth. It provides a step-by-step approach to calculating gravitational acceleration on a planet with three times the radius and four times the mass of Earth, resulting in a gravitational acceleration of 4/9 times that of Earth's. The escape speed comparison between Earth and another planet is also discussed, showing that the escape speed is dependent on the mass of the planet and independent of the object's mass.
🛰️ Satellite Orbits and Gravitational Force Inside a Uniform Planet
This section discusses the motion of a satellite in a circular orbit around Jupiter, using Newton's laws to derive the orbital speed and period. It also addresses the scenario of a satellite's orbit synchronized with Jupiter's rotation period, requiring specific calculations for the orbital radius. The script further explores the gravitational force on a small sphere moving freely inside a non-rotating, uniformly dense planet with a tunnel drilled through its diameter, deriving the force experienced by the sphere at various distances from the center of the planet.
📉 Work Done by Gravity and Sphere's Motion Inside a Planet
The script calculates the work done by gravity on a sphere as it moves from the surface to the center of a planet, using the derived expression for the force on the sphere. It explains that the work done translates into kinetic energy, allowing the calculation of the sphere's speed at the center of the planet. The subsequent motion of the sphere is described as oscillating back and forth within the tunnel without damping due to the absence of friction, adhering to Newton's first law of motion.
⏱️ Differential Equation for Sphere's Motion and Summary of Gravitational Concepts
The final paragraph outlines the process of deriving a differential equation for the motion of a sphere inside a planet, emphasizing that it's not necessary to solve the equation for the exam. It wraps up the session with a summary of key gravitational concepts, including Newton's universal law of gravitation, gravitational potential energy, mechanical energy conservation, angular momentum conservation in orbits, and Kepler's third law, highlighting their significance and applications in understanding celestial mechanics.
Mindmap
Keywords
💡Gravitation
💡Newton's Universal Law of Gravitation
💡Gravitational Acceleration
💡Gravitational Potential Energy
💡Escape Speed
💡Angular Momentum
💡Orbit
💡Kepler's Laws
💡Conservation of Energy
💡Torque
Highlights
Introduction to the concept of gravitation, specifically gravitational forces and orbits.
Explanation of Newton's Universal Law of Gravitation as the foundation of the unit.
Derivation of an expression for gravitational acceleration on any planet.
Introduction of a new expression for gravitational potential energy valid between any two objects.
Derivation of an expression for escape speed from a planet.
Discussion on the conservation of angular momentum in orbits.
Method to determine the period of a satellite's orbit.
Overview of Kepler's three laws in relation to planetary motion.
Clarification of the difference between lowercase 'g' for gravitational acceleration and uppercase 'G' for the gravitational constant.
Importance of the gravitational constant's small value in understanding the relative strength of gravitational force.
Explanation of why gravitational potential energy is negative and its relation to internal work done.
Derivation of the formula for escape speed and its independence from the mass of the object.
Illustration of how angular momentum conservation affects the speed of an orbiting satellite at different distances from the planet.
Detailed explanation of Kepler's First Law regarding elliptical orbits with the sun at one focus.
Description of Kepler's Second Law on equal areas being swept over equal time intervals by a planet.
Derivation of Kepler's Third Law from Newton's second law and its implications for orbital periods and radii.
Application of gravitational concepts to calculate the acceleration due to gravity on a hypothetical planet with different mass and radius compared to Earth.
Analysis of the escape speed of a hypothetical planet compared to Earth's, emphasizing the dependency on the planet's mass and radius.
Problem-solving approach for objects in motion within and outside a planet, including work done by gravity and resulting speeds.
Differential equation formulation for the motion of a sphere through a tunnel within a planet.
Summary of key takeaways from the gravitation lesson, including Newton's Law, gravitational potential energy, mechanical energy, angular momentum, and Kepler's laws.
Transcripts
Browse More Related Video

2021 Live Review 7 | AP Physics C: Mechanics | Angular Momentum & Rotational Collisions

2022 Live Review 6 | AP Physics C: Mechanics | Rotational Dynamics and Angular Momentum
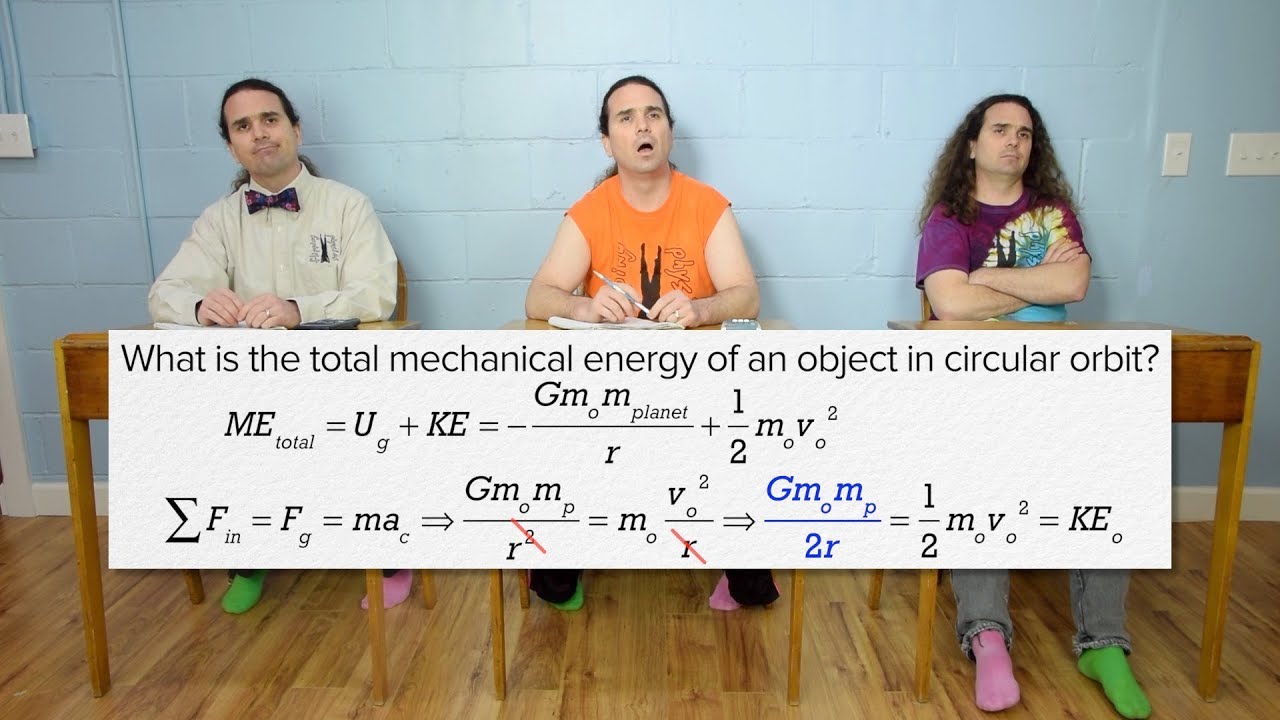
AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET

2022 Live Review 4 | AP Physics C: Mechanics | System of Particles and Linear Momentum

6 | FRQ | Practice Sessions | AP Physics C: Mechanics

2022 Live Review 3 | AP Physics C: Mechanics | Work, Energy, and Power
5.0 / 5 (0 votes)
Thanks for rating: