2 | FRQ | Practice Sessions | AP Physics C: Mechanics

Advanced Placement

17 Apr 202312:12

EducationalLearning

32 Likes 10 Comments

TLDRIn this instructional video, Dr. Julie Hood guides viewers through a physics problem involving potential and kinetic energy, momentum, and acceleration. She calculates the total mechanical energy of a 3 kg object moving along the x-axis with a given potential energy function, identifies positions with zero kinetic energy, and determines momentum and acceleration at specific points. The video also covers sketching graphs of position versus time and kinetic energy over time, highlighting the importance of understanding simple harmonic motion and energy conservation. Dr. Hood emphasizes the need for algebraic proficiency and correct application of physics concepts, especially for students preparing for exams.

Takeaways

📚 The video is an educational session focused on a numerical physics problem involving potential energy, mechanical energy, momentum, acceleration, and simple harmonic motion.
🔗 The audience is encouraged to download the PDF of the problem by clicking on the provided link for a more interactive experience.
📈 The potential energy function given is U(x) = 4x^2, where U is in joules and x is in meters, and it's used to calculate the total mechanical energy of a 3 kg object moving along the x-axis.
🚀 At x = -1/2 meter, the object has a velocity of 2 m/s, and this information is used to find the object's total mechanical energy at that position, which is 7 joules.
🔍 The problem requires finding the x-coordinates where the object's kinetic energy is zero, which are calculated to be at ±1.3 meters, based on the conservation of energy principle.
📐 The video demonstrates how to calculate the momentum of the object at a specific position (0.6 meters) using the conservation of energy and the given mass and potential energy function.
⏱ The acceleration at any point is derived from the potential energy function, and the magnitude of acceleration at x = 0.6 meters is found to be 1.6 m/s².
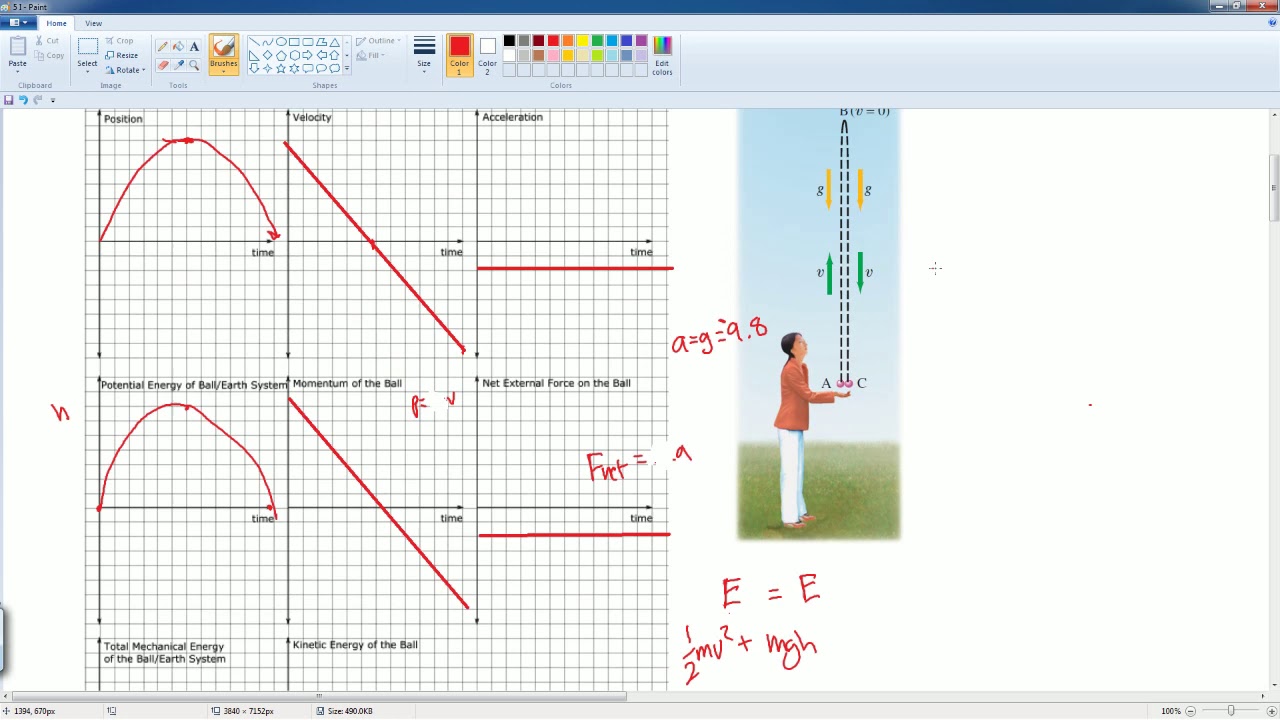
📊 The session includes sketching graphs of the object's position versus time and kinetic energy versus time, emphasizing the need to match trends and key points.
🌀 The object's motion is likened to simple harmonic motion, with acceleration being proportional to the negative displacement, leading to an oscillating system.
📉 The video highlights the importance of understanding the difference between simple harmonic motion and constant acceleration scenarios, noting that kinematic equations are not applicable in SHM.
💯 The session concludes with a reminder of the importance of practice and a gentle nudge for students to aim for full marks, especially with exams being only two weeks away.

Q & A

What is the main topic of the video presented by Dr. Julie Hood?
-The main topic of the video is to work through a numerical physics problem focusing on potential energy, mechanical energy, momentum, acceleration, and simple harmonic motion.
What is the potential energy function given for the 3-kilogram object moving along the x-axis?
-The potential energy function given for the object is U(x) = 4x^2, where U is in joules and x is in meters.
What is the velocity of the object when it passes the point at negative 1/2 a meter?
-The velocity of the object when it passes the point at negative 1/2 meter is 2 meters per second.
What is the total mechanical energy of the object in the system?
-The total mechanical energy of the object in the system is 7 joules, calculated by summing the potential energy (1 joule) and the kinetic energy (6 joules) at the given position.
How can you find the x-coordinates where the object has zero kinetic energy?
-To find the x-coordinates where the object has zero kinetic energy, set the kinetic energy to zero and solve for x in the potential energy equation, U(x) = 7 joules, which gives x = ±1.3 meters.
What is the magnitude of the momentum of the object at position 0.6 meters?
-The magnitude of the momentum of the object at position 0.6 meters is 5.76 kilogram meters per second, calculated using the mass (3 kg) and the velocity (1.92 m/s) at that position.
How do you calculate the acceleration at a given point using the potential energy function?
-To calculate the acceleration at a given point, take the derivative of the potential energy function with a negative sign to get the force function, and then divide by the mass of the object.
What is the magnitude of the acceleration when the object is at 0.6 meters?
-The magnitude of the acceleration when the object is at 0.6 meters is 1.6 meters per second squared.
Why is it incorrect to use kinematic equations for an object undergoing simple harmonic motion?
-Kinematic equations are incorrect for an object undergoing simple harmonic motion because these equations assume constant acceleration, which is not the case in simple harmonic motion where acceleration is proportional to the negative displacement.
What is the significance of the potential energy function being a parabola in this context?
-The significance of the potential energy function being a parabola is that it indicates the object will have two positions where the potential energy is zero, which corresponds to the points where the kinetic energy is at its maximum.
How does the video script suggest practicing for problems like the one presented?
-The video script suggests practicing by understanding and memorizing key equations, such as the relationship between potential energy, force, and acceleration, and by repeatedly working through similar problems to gain proficiency.

Outlines

00:00

📚 Introduction and Overview

Dr. Julie Hood, an AP Physics teacher at MAST Academy in Miami, Florida, introduces a video on solving a free response problem focused on potential energy. She outlines the topics to be covered, including mechanical energy, momentum, acceleration, graph sketching, and simple harmonic motion. The problem involves a 3 kg object moving along the x-axis with potential energy given by 4x squared, and various calculations will be performed.

05:03

🔢 Calculating Total Mechanical Energy

The first task is to find the total mechanical energy of the object, which involves adding potential and kinetic energy. Using the given potential energy function and the object's position and velocity, the potential energy at -1/2 meter is calculated as 1 joule and the kinetic energy as 6 joules, resulting in a total mechanical energy of 7 joules.

10:07

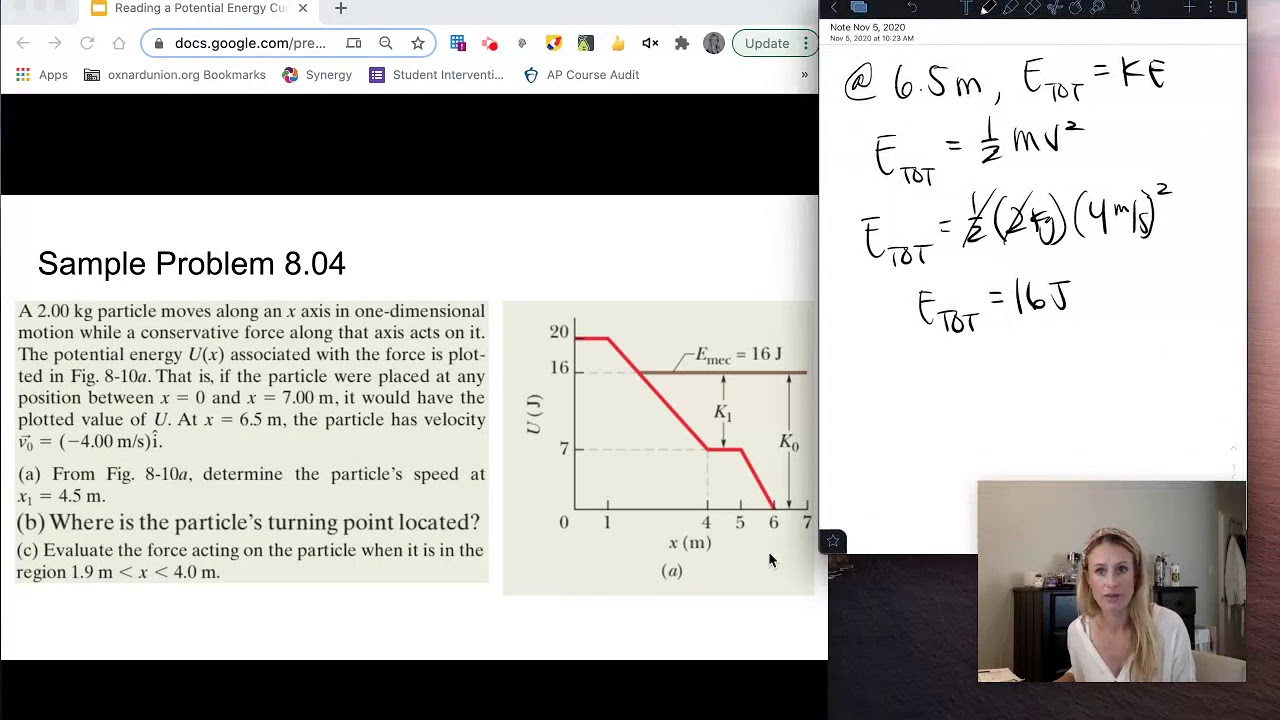
🧩 Finding Zero Kinetic Energy Points

To find the x-coordinates where the object has zero kinetic energy, it is noted that all energy will be potential energy, totaling 7 joules. By solving the potential energy equation 4x squared for 7 joules, it is found that the object can be at ±1.3 meters, reflecting the symmetry of the potential energy function.

🚀 Calculating Momentum

The next part involves calculating the object's momentum at 0.6 meters. Given the potential energy at this position and using the conservation of energy, the remaining kinetic energy is determined. With the kinetic energy known, the velocity is calculated and then used to find the momentum, which is 5.76 kg·m/s.

⚡ Determining Acceleration

The acceleration at 0.6 meters is calculated by finding the force from the potential energy function. Using the derivative of the potential energy function and applying Newton's second law, the acceleration is found to be 1.6 meters per second squared.

📈 Sketching Graphs

The final task is to sketch graphs of the object's position and kinetic energy versus time. Using the characteristics of simple harmonic motion, the position graph is a cosine function starting at the origin. The kinetic energy graph shows maxima at the points where the position crosses the time axis and zero kinetic energy at the position's maxima and minima. The importance of matching trends and key points is emphasized.

🔍 Common Errors and Misconceptions

Dr. Hood discusses common errors students make, such as poor algebra skills and incorrect application of kinematics equations for non-constant acceleration scenarios like simple harmonic motion. She emphasizes the need for practice and understanding the proper use of equations for different physical contexts. The review problem serves as a good practice for potential energy concepts.

Mindmap

Keywords

💡Potential Energy

Potential energy is the energy stored in an object due to its position in a force field, such as gravitational or elastic. In the video, Dr. Julie Hood discusses potential energy in the context of a 3-kilogram object moving along the x-axis, with the potential energy function given as 4x squared. This concept is crucial for understanding the mechanical energy calculations and the object's motion.

💡Kinetic Energy

Kinetic energy is the energy an object possesses due to its motion. Dr. Hood calculates the kinetic energy of a 3-kilogram object with a velocity of 2 meters per second. Understanding kinetic energy helps in determining the total mechanical energy of the system and analyzing the object's momentum and acceleration.

💡Mechanical Energy

Mechanical energy is the sum of potential and kinetic energy in a system. In the video, Dr. Hood explains how to calculate the total mechanical energy of a system, which remains constant if only conservative forces are acting. This concept is foundational for solving the problem and understanding energy conservation.

💡Momentum

Momentum is the product of an object's mass and velocity, representing the quantity of motion it has. Dr. Hood calculates the momentum of the object at a position of 0.6 meters. Momentum is used to analyze the object's movement and changes in velocity.

💡Acceleration

Acceleration is the rate of change of velocity of an object. It is determined by the forces acting on the object. Dr. Hood calculates the acceleration by taking the derivative of the potential energy function, highlighting the relationship between force and acceleration. This concept is key to understanding how the object's velocity changes over time.

💡Conservative Forces

Conservative forces are forces that do not dissipate energy and allow the total mechanical energy to be conserved in a system. Dr. Hood mentions that all forces acting on the object are conservative, ensuring that the total mechanical energy remains constant. This concept is important for energy conservation calculations.

💡Simple Harmonic Motion

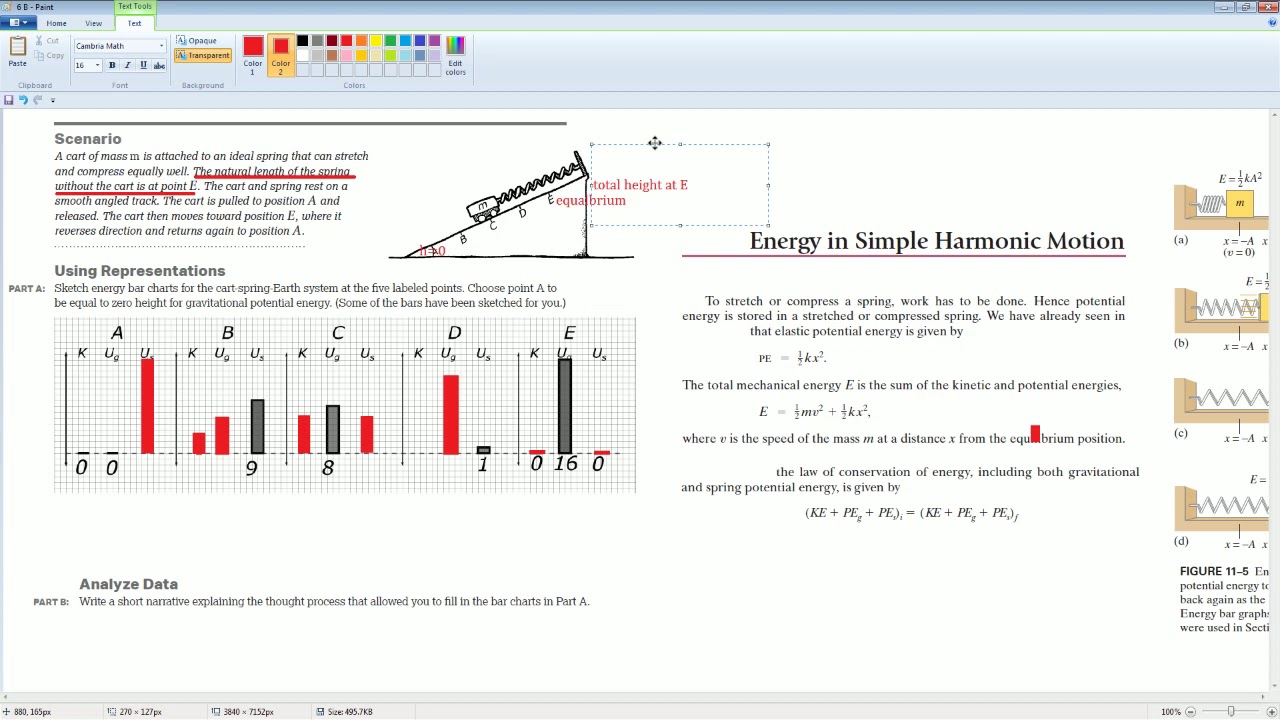
Simple harmonic motion is a type of periodic motion where the restoring force is proportional to the displacement and acts in the direction opposite to that displacement. Dr. Hood discusses simple harmonic motion in the context of the object's acceleration being proportional to the negative displacement, leading to an oscillating system. This concept is used to sketch graphs of position and kinetic energy versus time.

💡Energy Conservation

Energy conservation is the principle that the total energy in a closed system remains constant. Dr. Hood emphasizes that since only conservative forces act on the object, its total mechanical energy is conserved. This principle is fundamental for solving the problem and understanding the energy transformations within the system.

💡Graphing

Graphing involves plotting data points to visualize relationships between variables. Dr. Hood instructs on sketching graphs of the object's position versus time and kinetic energy versus time, emphasizing the importance of identifying trends and key points. Graphing helps in analyzing the motion and energy changes of the object.

💡Derivative

A derivative is a mathematical operation that calculates the rate at which a function is changing at any given point. Dr. Hood uses the derivative of the potential energy function to find the force acting on the object and subsequently its acceleration. Understanding derivatives is essential for analyzing changes in physical quantities.

Highlights

Introduction to a free response problem focused on potential energy in an AP Physics context.

Availability of a PDF download for the problem discussed in the video.

Explanation of calculating mechanical energy, including potential and kinetic energy, and momentum.

Introduction to simple harmonic motion as part of the problem-solving process.

Description of a 3 kg object moving along the x-axis with a given potential energy function.

Given conditions: object's velocity at -1/2 meter and the conservation of all forces.

Calculation of total mechanical energy using potential and kinetic energy formulas.

Determination of x-coordinates where the object's kinetic energy is zero.

Calculation of the object's momentum at a specific position (0.6 meters).

Derivation of acceleration from the potential energy function using calculus.

Emphasis on the importance of understanding and applying conservation of energy.

Guidance on sketching graphs for position versus time and kinetic energy versus time.

Discussion on the relationship between acceleration and displacement in simple harmonic motion.

Calculation of the period of oscillation for the object using its mass and the derived formula.

Advice on avoiding common algebra mistakes and the importance of practice.

Warning against using kinematics equations for non-constant acceleration scenarios.

Encouragement for students to aim for full marks as they approach their exams.

Transcripts

Browse More Related Video

2015 AP Physics 1 free response 3a

AP Physics Workbook 5.I Momentum Representations

2022 Live Review 6 | AP Physics C: Mechanics | Rotational Dynamics and Angular Momentum

3 | FRQ | Practice Sessions | AP Physics C: Mechanics

Potential Energy Graph Example

AP Physics Workbook 6.B Simple Harmonic Motion and Energy Review