2021 Live Review 3 | AP Physics C: Mechanics | Graphing Simple Harmonic Motion
TLDRThis video script from an AP Daily Live Review session for Physics C Mechanics delves into the concept of simple harmonic motion, focusing on the derivation of differential equations for oscillators, including springs and pendulums. It explains how to combine springs in series and parallel, explores the equations of motion, and emphasizes the importance of understanding the relationship between acceleration and displacement. The session also covers experimental design for a torsional pendulum, providing insights into data analysis and graphing techniques to determine physical properties like the torsion constant.
Takeaways
- 📚 A differential equation is an equation that relates a function to its derivatives, often used to describe physical systems like simple harmonic motion.
- 🌀 Simple harmonic motion is characterized by acceleration being proportional to displacement but in the opposite direction, with the proportionality constant being the square of the angular frequency (ω²).
- ⚖️ The angular frequency (ω) is defined as 2π divided by the period of oscillation, which is the time for one complete oscillation.
- 📉 The equations of motion for a simple harmonic oscillator can be sinusoidal, using either cosine or sine functions, depending on the initial conditions of the system.
- 🔍 In a torsional pendulum experiment, the restoring torque is proportional to the angular displacement (θ), and the differential equation governing its motion can be derived from Newton's second law for rotation.
- 🔧 When combining springs in parallel, the effective spring constant is the sum of the individual spring constants, allowing for a simpler representation of the system's behavior.
- 🔗 In contrast, combining springs in series requires a more complex calculation where the effective spring constant is found by summing the inverses of each spring constant and then taking the reciprocal.
- 📏 The period of a pendulum can be determined using the formula T = 2π √(l/g), which assumes small angles of oscillation and can be derived from the small angle approximation of sine.
- 🔬 Experimental design is crucial for minimizing uncertainty in measurements, such as timing multiple oscillations to reduce the impact of reaction time on the measurement of period.
- 📉 When graphing data from a torsional pendulum experiment, plotting the square of the period (T²) against the rotational inertia (I) and fitting a straight line can help determine the torsion constant (β).
- 🔍 The maximum speed of an object on a spring, oscillating on a frictionless surface, is directly related to the square root of the spring's force constant and the amplitude of oscillation.
Q & A
What is a differential equation and how is it related to simple harmonic motion?
-A differential equation is an equation that relates a function to its derivatives. In the context of simple harmonic motion, it is used to describe the motion of an object where the acceleration is proportional to the displacement but in the opposite direction. The differential equation for such a system can be derived by applying Newton's second law and replacing acceleration with the second derivative of position.
What is the definition of simple harmonic motion?
-Simple harmonic motion is defined as a type of periodic motion where the acceleration of the object is directly proportional to its displacement from the equilibrium position, but in the opposite direction. The proportionality constant is the square of the angular frequency (ω²).
How can you derive the equation of motion for a simple harmonic oscillator?
-The equation of motion for a simple harmonic oscillator can be derived by assuming the oscillator starts at the amplitude and using the cosine function, which starts at its maximum value. The velocity is the time derivative of position, and differentiating once more gives the acceleration, which can be expressed in terms of the angular frequency and the position function.
What is the relationship between angular frequency and the period of oscillation?
-The angular frequency (ω) is related to the period (T) of oscillation by the equation ω = 2π / T. The period is the time it takes for the object to complete one full oscillation.
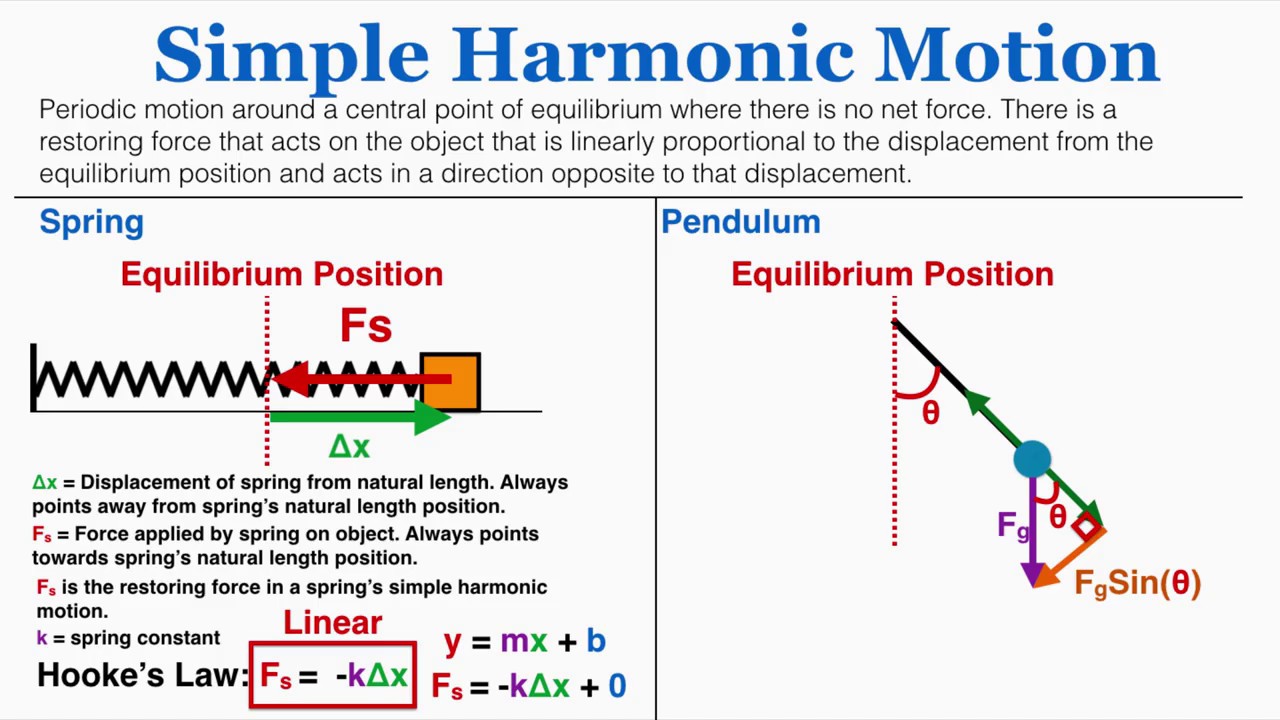
How does the restoring force in a spring-mass system contribute to the differential equation?
-In a spring-mass system, the restoring force is the spring force that acts to bring the object back to its equilibrium position. This force is proportional to the displacement from equilibrium and is included in the differential equation by substituting it for the force term in Newton's second law and then replacing acceleration with the second derivative of position.
What is the small angle approximation and how is it used in the study of pendulums?
-The small angle approximation states that for small angles, the sine of an angle (θ) is approximately equal to the angle itself in radians. This approximation is used in the study of pendulums to simplify the restoring force, which is the component of the gravitational force tangent to the arc of the pendulum's swing.
How can you combine springs in parallel and what is the effective spring constant?
-When combining springs in parallel, the effective spring constant is the sum of the individual spring constants. This is because each spring contributes equally to the restoring force when the system is displaced from equilibrium.
What is the process for combining springs in series and what is the effective spring constant in this case?
-When combining springs in series, the effective spring constant is found by taking the sum of the inverses of each individual spring constant and then inverting this sum. This results in a more complex relationship due to the division of displacement between the springs.
How can you determine the period of a torsional pendulum?
-The period of a torsional pendulum can be determined by using the differential equation derived from the restoring torque and the moment of inertia of the pendulum. By comparing this equation to the standard form of simple harmonic motion, the angular frequency can be found, and subsequently, the period using the relationship between angular frequency and period.
What is the significance of the negative sign in the differential equation for a simple harmonic oscillator?
-The negative sign in the differential equation indicates that the acceleration of the oscillator is in the opposite direction to the displacement from equilibrium. This is a key characteristic of simple harmonic motion, where the restoring force always acts to return the object to its equilibrium position.
How can you minimize the uncertainty in measurements when conducting a pendulum experiment?
-To minimize uncertainty in pendulum experiments, one should measure over multiple oscillations rather than just one, as this averages out any small errors in timing. Additionally, starting the pendulum from small angles ensures that the small angle approximation holds, leading to more accurate results.
Outlines
📚 Introduction to Simple Harmonic Motion and Differential Equations
The video begins with an introduction to simple harmonic motion, which is a type of oscillatory motion where the restoring force is proportional to the displacement and in the opposite direction. The presenter explains the concept of a differential equation, which is an equation involving a function and its derivatives, using the example of a spring-block system. The video promises to cover topics such as the definition of simple harmonic motion, experimental design for a torsional pendulum, and examples of simple harmonic oscillators like a pendulum and a spring system. The audience is advised to watch the unit 6 videos on AP Classroom for foundational knowledge before proceeding with practice problems in the video.
🔍 Exploring the Dynamics of Simple Harmonic Oscillators and Pendulums
This paragraph delves deeper into the dynamics of simple harmonic oscillators, focusing on the differential equation derived from Newton's second law for a block attached to a spring. The presenter clarifies the definition of simple harmonic motion, where acceleration is proportional to displacement with a constant of proportionality being the square of the angular frequency (ω²). The equations of motion for a simple harmonic oscillator are discussed, including the position, velocity, and acceleration as functions of time, using cosine and sine functions to represent the motion. The importance of the initial conditions in choosing between cosine and sine for the position function is highlighted, with examples provided to illustrate the concepts.
🌐 Understanding the Forces and Motion of a Pendulum
The discussion shifts to the mechanics of a pendulum, specifically a simple pendulum with a mass at the end of a massless string. The presenter explains the forces acting on the pendulum bob, including gravity and the tension in the string, and identifies the restoring force as the component of gravitational force tangential to the arc of motion. Using Newton's second law, a differential equation for the pendulum's motion is derived, leading to an expression for the angular frequency of the pendulum. The small angle approximation is introduced to simplify the equation, and the period of the pendulum is calculated based on this approximation, with a caution about the limitations of this approximation for larger angles.
🔧 Combining Springs in Parallel and Series: Effective Spring Constants
The video explores how to combine springs in both parallel and series configurations. When springs are connected in parallel, their spring constants are simply added together to find the effective spring constant. In contrast, for springs in series, the effective spring constant is found by taking the sum of the inverses of each spring constant and then inverting this sum. The presenter provides a step-by-step explanation of how to calculate the effective spring constant for both scenarios, emphasizing the importance of correctly inverting the sum of inverses when combining springs in series.
📐 Analyzing Torsional Pendulums and Their Differential Equations
The presenter introduces the concept of a torsional pendulum, which involves a disk with rotational inertia twisted by an angle and released to oscillate. The restoring torque is given as a function of the angular displacement, and the presenter demonstrates how to write a differential equation for this system by substituting the torque into the rotational equivalent of Newton's second law. The period of the torsional pendulum is derived by comparing the differential equation to the standard form of simple harmonic motion, and an analogy to a linear mass-spring system is used to determine the period.
📉 Data Analysis and Graphing for Torsional Pendulum Experiments
This section focuses on the experimental design and data analysis for a torsional pendulum. The presenter explains how to plot data on a graph to determine the torsion constant, emphasizing the importance of graphing the square of the period versus the rotational inertia to linearize the data. The presenter also discusses the significance of measuring multiple oscillations to reduce uncertainty in the measurement and how to calculate the period and the slope of the best-fit line to find the torsion constant. The physical meaning of the vertical intercept on the graph is explored, relating it to the properties of the flexible rod without a disk.
🤔 Reflecting on the Properties and Errors in Pendulum Experiments
The video addresses common sources of error in pendulum experiments, such as releasing the pendulum from too large an angle, which can lead to inaccuracies in the period measurement. The presenter also discusses the impact of using the average of multiple oscillations to reduce uncertainty and the importance of graphing the data to obtain a straight line for analysis. The presenter provides a step-by-step guide on how to approach pendulum problems, including determining acceleration at a given time and the effect of changing the length of the pendulum on its period.
🔄 True or False: Understanding the Behavior of Oscillating Systems
This paragraph presents a series of true or false questions related to the behavior of oscillating systems, such as blocks on springs and pendulums. The presenter clarifies misconceptions about the velocity and acceleration at equilibrium and amplitude, emphasizing the importance of understanding the relationship between displacement, velocity, and acceleration in simple harmonic motion. The questions serve to reinforce the concepts learned throughout the video and to test the viewer's comprehension of the material.
🔄 Further Exploration of Spring Systems and Their Dynamics
The video concludes with a more complex problem involving springs in both parallel and series configurations, as well as a massless spring on a frictionless surface. The presenter demonstrates how to calculate the effective spring constant for these systems and how to apply Newton's second law to derive the differential equation governing the motion. The relationship between the amplitude, frequency, and force constant of the spring is explored, and the presenter provides a method for determining the force constant given the amplitude and frequency of the oscillation.
🚀 Conclusion: Recap of Simple Harmonic Motion and Spring Systems
In the final paragraph, the presenter summarizes the key takeaways from the video, which include understanding the definition and properties of simple harmonic motion, the ability to write differential equations for oscillatory systems, and the methods for combining springs in both parallel and series configurations. The importance of recognizing the direction of acceleration relative to displacement and the sinusoidal nature of the equations of motion is reiterated. The presenter also reminds viewers of the upcoming topic on non-linear springs, setting the stage for further learning.
Mindmap
Keywords
💡Differential Equation
💡Simple Harmonic Motion (SHM)
💡Angular Frequency (ω)
💡Restoring Force
💡Torsional Pendulum
💡Parallel Springs
💡Series Springs
💡Amplitude
💡Period
💡Oscillator
Highlights
Introduction to the topic of simple harmonic motion and its importance in physics.
Definition of a differential equation and its relation to simple harmonic motion.
Explanation of Newton's second law applied to a spring-mass system to derive a differential equation.
The definition of simple harmonic motion with acceleration proportional to displacement in the opposite direction.
Derivation of the angular frequency equation and its relationship with the period of oscillation.
Equations of motion for a simple harmonic oscillator, including position, velocity, and acceleration.
Discussion on the properties of a pendulum as a simple harmonic oscillator and the restoring force involved.
Use of the small angle approximation in pendulum motion and its impact on the restoring force.
Combining springs in parallel and series, with the sum of spring constants and their inverses, respectively.
Experimental design for a torsional pendulum, including the differential equation for angular displacement.
Calculation of the period of a torsional pendulum using the derived differential equation.
Data analysis techniques for determining the torsion constant from a graph of period squared versus rotational inertia.
Error minimization in experimental design by measuring multiple oscillations and averaging.
Understanding the physical meaning behind the graph intercepts and the implications for a system without a pendulum bob.
Analysis of the relationship between the amplitude of oscillation and the maximum speed of a simple harmonic oscillator.
Combining springs in series and parallel to find the effective spring constant and its impact on oscillatory motion.
Determination of the spring constant for an ideal massless spring on a frictionless surface using energy conservation.
Graph interpretation for the relationship between acceleration and displacement in simple harmonic motion.
Correct representation of Newton's second law in a differential equation for a simple harmonic oscillator.
Conclusion summarizing the key takeaways from the video, including the nature of simple harmonic motion and spring combinations.
Transcripts
Browse More Related Video

2021 Live Review 6 | AP Physics 1 | Understanding Simple Harmonic Motion

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion

Simple harmonic motion and angular frequency [IB Physics SL/HL]

2022 Live Review 6 | AP Physics 1 | Understanding Simple Harmonic Motion
Simple Harmonic Motion - IB Physics

2021 Live Review 8 | AP Physics C: Mechanics | Understanding Resistive Forces
5.0 / 5 (0 votes)
Thanks for rating: